• American Fuzzy Lop
• Fuzzing With AFL-Fuzz, a Practical Example ( AFL vs Binutils )
• Fuzzing with American Fuzzy Lop (AFL)
• Concolic execution with S2E
• angr documentation (GitHub link)
• angr overview
• angr -- claripy solver engine
• angr -- program states
• angr -- path groups
• angr -- working with data and conventions
• angr examples

We will use this lab archive throughout the lab.

Please download the lab archive an then unpack it using the commands below:

spyked@tuvok:~% wget http://elf.cs.pub.ro/oss/res/labs/lab-13.tar.gz
spyked@tuvok:~% tar xzf lab-13.tar.gz

After unpacking we will get the lab-13/ folder that we will use for the lab:

spyked@tuvok:~% cd lab-13 
spyked@tuvok:~/lab-13% ls -F
0-tutorial/  1-baby-re/  2-hash/

So far our analysis techniques and tools of the trade have been very basic. Traditionally, binary analysis relies on disassembling executables, searching for data in binaries, dumping and searching memory in live processes and observing program control flow, e.g. by using a debugger. This is the bare minimum that we must do in order to find bugs (and hopefully, from our attacker's mindset, vulnerabilities), but these methods are often laborious and they do not scale to large programs. For example, looking for vulnerabilities in a large project such as a web server, an operating system kernel or a compiler might require weeks or even months to understand the (source or binary) code and this would give us no guarantees that we haven't missed a critical bug.

Intuitively, we should be able to partially automate the analysis process. We know that a program may crash (and may be potentially exploitable) in response to some specific inputs, e.g. a very long string, a big number, a malformed file or a combination between these. The problem of finding vulnerabilities then becomes: what are the specific inputs that make a program exploitable? In this lab we'll discuss two fundamental approaches for this problem:

• Fuzz testing
• Symbolic execution

To understand how fuzz testing works, let's start from the following simple program written in C, reminiscent of the integers lab:

level07.c

#include <stdio.h>
#include <string.h>
#include <unistd.h>
 
int main(int argc, char **argv)
{
    int count = atoi(argv[1]);
    int buf[10];
 
    if(count >= 10 ) 
        return 1;
 
    memcpy(buf, argv[2], count * sizeof(int));
    if(count == 0x574f4c46) {
        printf("WIN!\n");
    } else
        printf("Not today son\n");
 
    return 0;
}

The program receives a number and an arbitrary string as arguments; count = atoi(argv[1]) represents the length of the string stored in argv[2]. The program copies argv[2] into a local variable buf, which we hope to be able to overflow into count in order to make count == 0x574f4c46 become true. We know that the vulnerability comes from an integer overflow: count is a signed integer, but count * sizeof(int) is an unsigned integer (size_t), so by giving a large negative number as input, we can make count * sizeof(int) overflow into a small enough number. In fact we can make count * sizeof(int) be precisely 44.

This bug is easy to understand, but how do we find it automatically? The most intuitive approach would be to brute-force count and argv[2], i.e. try:

• ./level07 -1 an_input_string
• ./level07 -2 another_input_string
• …
• ./level07 -1073741813 "aaaaa...FLOW" (our desired example)

Modern fuzzers provide a more informed approach to brute-forcing, by:

• using evolutionary algorithms to explore the input space;
• keeping information about the internal program state (e.g. the paths exercised by specific inputs) by using compiler instrumentation;
• providing the possibility to (partially or totally) specify the input grammar in a dictionary, and/or automatically synthesizing the input grammar.

Examples of binary application fuzzers include: AFL, zzuf and boofuzz.

We have seen that fuzz testing doesn't perform well in exploring all the paths in the control flow graph of a program. The reason is that at run-time some inputs might only rarely or never trigger the execution of a certain path, and the best the fuzzer can do is try to guess what inputs would drive the program to execute some given code.

Symbolic execution is a program analysis tool that tries to exhaustively explore the control flow paths in a given program. The program is not executed per se, but it is interpreted in the following manner:

• Program inputs are associated with abstract symbols rather than concrete values.
• At each branching condition, the program state is forked: one state is associated with the case when the branch is taken and the associated constraint is stored for the variable upon which the condition is based; the other state is associated with the case when the branch is not taken, and the negation of the constraint is stored for the same variable; each of the states is explored separately.
• When the exploration of a path ends, a solver tries to satisfy all the constraints generated on that path, and paths that resolve to a contradiction are discarded as unsatisfiable; otherwise, concrete values are generated for some or all of the symbols (a step which is known as concretization).

Let's illustrate how our level07 program would be explored by a symbolic execution engine. We have two inputs, argv[1] and argv[2] whose values we don't know. We thus give them symbolic values, by applying the constraints argv[1] = α and argv[2] = β. Additionally, argv[1] is converted using atoi, which will generate another constraint, γ = atoi(α); and buf will be associated with another symbolic value, δ. The exploration of all the paths is shown in the figure below.

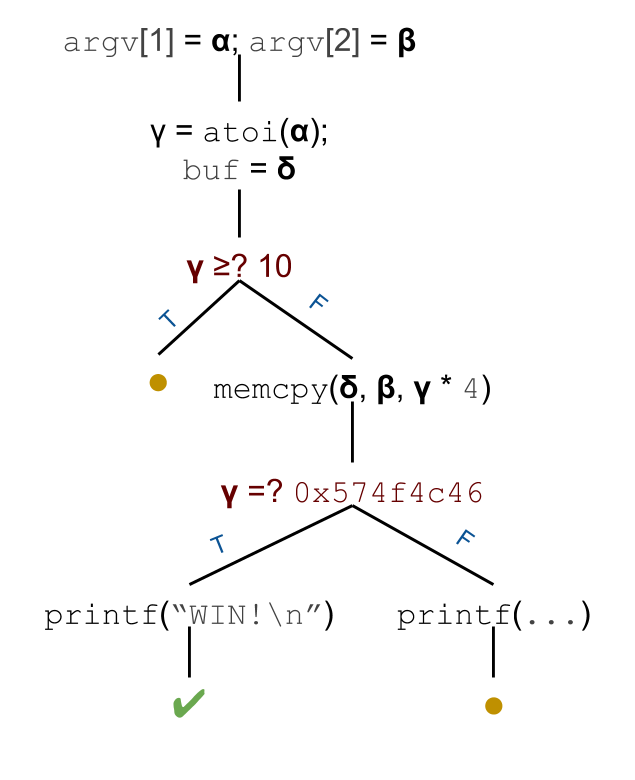
We denote the target state in our symbolic execution (the one in which printf("WIN!\n"); has been called) using a check mark (✔) and dead ends using a circle (●). The path we are looking for seems unsatisfiable at a first look (γ < 10 and γ = 0x574f4c46), but in fact the call to memcpy, for certain values values of β and γ, will generate a state where δ (the symbolic value associated with buf) will have overflown into γ.

When the symbolic execution ends (assuming it ended without errors), we can look at the target state and concretize any of the symbolic variables in the program. For example γ will obviously resolve to 0x574f4c46. α and β will resolve to an input, or a set of inputs, that trigger the execution path we're looking for.

Examples of symbolic execution engines include Angr, KLEE, Kite, Mayhem and S2E.

First, install angr. See http://angr.io/install.html.

sudo apt-get install python-dev libffi-dev build-essential virtualenvwrapper

$ # replace the following with your favourite Python virtualenv directory
$ export WORKON_HOME=~/.environments
$ # replace the following with your virtualenvwrapper.sh location if needed
$ source /usr/share/virtualenvwrapper/virtualenvwrapper.sh

$ mkvirtualenv angr

(angr) $ pip install angr

$ workon angr
(angr) $ python my_angr_script.py

...
ImportError: cannot import name arm

Then let's go to the 0-tutorial folder, which contains level07 and level07.c. We also have an example solver script called solver.py. Let's take a look at it.

angr organizes binary analyses into projects. Creating a new angr project is as simple as:

b = angr.Project('./level07')

First, we want to generate the arguments that we will pass to level07. The arguments can be concrete (e.g. Python strings, integers, etc.) or symbolic. We're lazy, so let's pass the two arguments as symbolic variables. angr uses claripy as a solver engine, so we will instantiate the arguments using it:

arg1 = claripy.BVS('sym_arg', 8 * 11) # maximum 11 * 8 bits
arg2 = claripy.BVS('sym_arg', 8 * 44) # maximum 44 * 8 bits

where arg1 is a symbolic value (BVS) of 11 bytes, and arg2 is another symbolic value, of 44 bytes. Note that we are passing arg1 as a string, and decimal int numbers passed to level07 are at most 11 bytes in length.

Next, we want to create an initial state to start from. angr uses SimuVEX to represent program state, which includes a low-level architecture-dependent representation of the binary we're analyzing. angr provides a factory object to generate our initial state:

st = b.factory.entry_state(args=['./level07', arg1, arg2])
st.libc.max_strtol_len = 11 # tweak

st will be our new state.

Now we will create what in angr terms is called a path group. A path group is an object that we can use to explore paths in our program. We will create our new path group pg starting from st:

pg = b.factory.path_group(st)

At this point we can instruct the symbolic execution engine to:

• perform a single step – pg.step()
• perform a number of steps – e.g. pg.run(n=20) to run at most 20 steps
• run until all paths have been executed – pg.run()
• explore until a solution has been found – e.g.
  • pg.explore(find=0x804846b) will try to find a path that leads to 0x804846b
  • pg.explore(find=lambda path : my_predicate(path))) will try to find a path that satisfies my_predicate
  • pg.explore(find=addr1, avoid=addr2) will try to find a path that leads to addr1 and avoid all paths that lead to addr2

We want to find a path where the string "WIN!\n" is printed to standard output. Thus we will do:

pg.explore(find=lambda p: "WIN" in p.state.posix.dumps(1))

This can be read as: explore looking for the path p for which the current state p.state contains the string "WIN" in its standard output (p.state.posix.dumps(1), where 1 is the file descriptor for stdout).

After execution is done, we can print pg, getting something such as:

pg = <PathGroup with 1 deadended, 1 active, 1 found>

This tells us that pg contains exactly 1 path which reached the end, 1 path left to explore and 1 path for which a solution was found. At this point we could further explore along the active path, but we don't need to do that.

Given that we have a found path, let's look at the current state in this path:

s = pg.found[0].state

We can do a lot of things with s, including:

• inspecting file descriptor streams, e.g. s.posix.dumps(n), where n is a file descriptor number
• inspecting registers, e.g. s.regs.eax
• inspecting memory, e.g. s.mem[0x7ffeff18]
• using the solver (s.se) to concretize symbolic values

We want to concretize arg1 and arg2 and print them, i.e.:

print "arg1 = {} ".format(repr(s.se.any_str(arg1)))
print "arg2 = {} ".format(repr(s.se.any_str(arg2)))

What we do here is instruct the solver to give us the string representation of the first solution it finds from solving constraints, for each of arg1 and arg2. See Program states for more info on how s.se works.

The output of our concretization will be:

arg1 = '-2147483627'
arg2 = '\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00FLOW'

Let's try these out:

$ ./level07 -2147483627 $(echo -ne '\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00FLOW')
WIN!
segmentation fault

$ ./level07 -2147483627 $(python -c 'print "A"*40 + "FLOW"')
WIN!
segmentation fault

We value your opinions and input on improving the Computer and Network Security class (CNS) and its components. Please take the time and fill the feedback form on cs.curs.pub.ro. Your feedback is very important for us to improve both the CNS class and other classes you will go through in the future.

We are particularly interested in:

• What didn't you like and what you consider didn't go well?
• Why didn't you like that and why you consider it didn't go well?
• What should we do to make things likable and going well?

Thank you!

We're given a binary (1-baby-re/baby-re) that we want to reverse engineer, the end result being a flag. Running the program, we see that it asks us for some inputs:

$ ./baby-re 
Var[0]: 1
Var[1]: 2
Var[2]: 3
Var[3]: 4
Var[4]: 5
Var[5]: 6
Var[6]: 7
Var[7]: 8
Var[8]: 9
Var[9]: 0
Var[10]: 1
Var[11]: 2
Var[12]: 3
Wrong

Before trying to execute it symbolically, let's try to inspect it. We have all the options that we know from the previous labs:

• disassembling it;
• strace-ing it;
• looking at the ELF header, symbols, strings, etc.;
• running it with GDB and inspecting memory, etc.

Since the program outputs some strings, let's look at it with strings. We notice that the programmer defined the following strings:

$ strings baby-re | grep -v '^_\|^\.\|GLIBC\|\.so'
...
Var[0]:
Var[1]:
Var[2]:
Var[3]:
Var[4]:
Var[5]:
Var[6]:
Var[7]:
Var[8]:
Var[9]:
Var[10]:
Var[11]:
Var[12]:
The flag is: %c%c%c%c%c%c%c%c%c%c%c%c%c
Wrong
...
CheckSolution
main

The string starting with "The flag is: " is what we want to see printed. Let's look a bit at the program flow, using objdump. Looking at main, we see that there are a lot of scanfs performed (the ones that get Var[0], Var[1], and so on), and then CheckSolution is called. We're interested in this particular piece of the code:

00000000004025e7 <main>:
  4028dd:       48 89 c7                mov    rdi,rax
  4028e0:       e8 e1 dd ff ff          call   4006c6 <CheckSolution>
  4028e5:       84 c0                   test   al,al
  4028e7:       74 58                   je     402941 <main+0x35a>
 ...
  402924:       45 89 f1                mov    r9d,r14d
  402927:       45 89 e8                mov    r8d,r13d
  40292a:       89 c6                   mov    esi,eax
  40292c:       bf 88 2a 40 00          mov    edi,0x402a88
  402931:       b8 00 00 00 00          mov    eax,0x0
  402936:       e8 45 dc ff ff          call   400580 <printf@plt>
  40293b:       48 83 c4 40             add    rsp,0x40
  40293f:       eb 0a                   jmp    40294b <main+0x364>
  402941:       bf b1 2a 40 00          mov    edi,0x402ab1
  402946:       e8 15 dc ff ff          call   400560 <puts@plt>
  40294b:       b8 00 00 00 00          mov    eax,0x0
  402950:       48 8b 5d d8             mov    rbx,QWORD PTR [rbp-0x28]
  402954:       64 48 33 1c 25 28 00    xor    rbx,QWORD PTR fs:0x28
...

We notice that at 0x4028e7 we have a check that jumps at 0x402941 if a condition is set. The code at 0x402941 in turns calls puts (not printf; in fact, we can assume this is where "Wrong" is printed.), which means that is not the code that prints the flag. So that is a path that we want to avoid.

If we get at 0x40293b, however, then it means printf will have been called, and we can assume this is what prints the flag. Then a jump to 0x40294b will be performed, which leads to the end of the program.

Now we know exactly what path we want to find (a path ending in 0x40293b or 0x40294b), and what paths we want to avoid (all the paths where puts("Wrong"); is executed).

Given this information, your task is to fill in solve_skel.py with an angr script that solves the riddle and makes the program print out the flag. Remember that in this case we don't need to find out the exact inputs that print out the solution; we only care about the flag, which is printed to standard output (path_groups.found[0].state.posix.dumps(1)).

Switch to 2-hash. The task performs a hash on the input and overwrites the return address with the function output. Use this to jump to the win function.

1. Solve the task by hand [2p]
2. Solve the task using the provided angr skeleton script [3p]