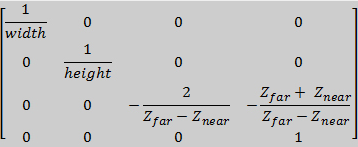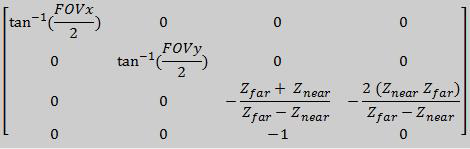Laboratorul 05
Video Laborator 5: https://youtu.be/HOv-P8QnEAA
Autor: Florin Iancu
Spațiul obiectului
Spațiul obiectului mai este denumit și SPAȚIUL COORDONATELOR LOCALE.
Pentru a putea lucra mai eficient și a reutiliza obiectele 3D definite, în general, fiecare obiect este definit într-un sistem de coordonate propriu. Obiectele simple sau procedurale pot fi definite direct din cod însă majoritatea obiectelor utilizate în aplicațiile 3D sunt specificate în cadrul unui program de modelare precum 3D Studio Max, Maya, Blender etc. Definind independent fiecare obiect 3D, putem să îi aplicăm o serie de transformări de rotație, scalare și translație pentru a reda obiectul în scena 3D. Un obiect încărcat poate fi afișat de mai multe ori prin utilizarea unor matrici de modelare, câte una pentru fiecare instanță a obiectului inițial, ce mențin transformările 3D aplicate acestor instanțe.
În general, fiecare obiect 3D este definit cu centrul (sau centrul bazei ca în poza de mai jos) în originea propriului său sistem de coordonate, deoarece în acest fel pot fi aplicate mai ușor transformările de modelare. Astfel, rotația și scalarea față de centrul propriu sunt efectuate întotdeauna față de origine.
Spațiul lumii
Transformarea din spațiul obiectului în spațiul lumii sau SPAȚIUL COORDONATELOR GLOBALE se numește transformare de modelare. Despre forma ei matriceală, cunoscută sub numele de matrice de modelare, s-a discutat mai sus. Matricea se obține printr-o serie de rotații, scalări și translații. Prin înmulțirea fiecărui vertex al unui obiect (mesh 3D) cu această matrice, obiectul va fi mutat din spațiul local în spațiul lumii, adică se face trecerea de la coordonate locale la coordonate globale.
Folosind matrici de modelare diferite putem amplasa un obiect în scenă de mai multe ori, în locații diferite, cu rotație și scalare diferită dacă este necesar. Un exemplu este prezentat în scena de mai jos.
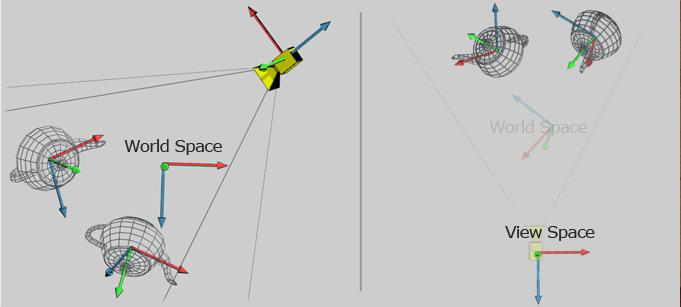
Spațiul de vizualizare
Transformarea din spațiul lumii în spațiul de vizualizare sau SPAȚIUL CAMEREI este cunoscută sub numele de transformare de vizualizare.
Matricea de modelare poziționează obiectele în scenă, în spațiul lumii. Dar o scenă poate fi vizualizată din mai multe puncte de vedere. Pentru aceasta există transformarea de vizualizare. Dacă într-o scenă avem mai multe obiecte, fiecare obiect are o matrice de modelare diferită (care l-a mutat din spațiul obiectului în spațiul lume), însă toate obiectele au aceeași matrice de vizualizare. Transformarea de vizualizare este definită pentru întreaga scenă.
În spațiul lumii, camera poate să fie considerată ca un obiect având cele 3 axe locale OX, OY, OZ (vezi poza). Matricea de vizualizare se poate calcula folosind funcția glm::lookAt.
glm::mat4 View = glm::lookAt(glm::vec3 posCameraLume, glm::vec3 directieVizualizare, glm::vec3 cameraUP);

Ox,Oy,Oz sunt axele sistemului de coordonate ale lumii (spațiul scenei 3D). Punctul O nu este marcat în imagine. O’x’,O’y’,O’z’ sunt axele sistemului de coordonate al observatorului (spațiul de vizualizare). Punctul O’ nu este marcat în imagine (este înăuntrul aparatului).
Vectorul forward este direcția în care observatorul privește, și este de asemenea normala la planul de vizualizare (planul fiind baza volumului de vizualizare, ce seamănă cu o piramidă și este marcat cu contur portocaliu). Vectorul right este direcția dreapta din punctul de vedere al observatorului. Vectorul up este direcția sus din punctul de vedere al observatorului.
În imagine, observatorul este un pic înclinat, în mod intenționat, în jos, față de propriul sistem de axe. Când observatorul este perfect aliniat cu axele, right coincide cu +x’, up coincide cu +y’, iar forward coincide cu -z’. În imagine, se poate vedea că up nu coincide cu +y’, iar forward nu coincide cu -z’.
Vectorul “up” se proiectează în planul de vizualizare, cu direcția de proiecție paralelă cu normala la planul de vizualizare. Proiecția acestuia dă direcția axei verticale a planului de vizualizare.
În spațiul lumii camera poate fi considerată un simplu obiect 3D asupra căruia aplicăm transformările de rotație și translație. Dacă în spațiul lumii, camera poate fi poziționată oriunde și poate avea orice orientare, în spațiul de vizualizare (spațiul observator) camera este întotdeauna poziționată în (0,0,0) și privește în direcția OZ negativă.
Matricea de vizualizare conține transformări de rotație și translație, la fel ca și matricea de modelare. De aceea, dacă ținem scena pe loc și mutăm camera, sau dacă ținem camera pe loc și rotim/translatăm scena, obținem același efect:
- Futurama
Totuși, cele două matrici au scopuri diferite. Una este folosită pentru poziționarea obiectelor în scenă, iar cealaltă pentru vizualizarea întregii scene din punctul de vedere al camerei.
glm::lookAt(glm::vec3(3, 5, 7), glm::vec3(1, 0, 0), glm::vec3(0, 1, 0));
Proiecții
După aplicarea transformării de vizualizare, în spațiul de vizualizare, camera se află în origine și privește înspre –OZ. Pentru a putea vizualiza pe ecran această informație este necesar să se facă proiecția spațiului vizualizat de cameră într-un spațiu 2D. Cum spațiul vizibil al camerei poate fi de diferite feluri, cel mai adesea trunchi de piramida (proiecție perspectivă) sau paralelipiped (proiecție ortografică), în OpenGL este necesară trecerea într-un spațiu final numit spațiu de proiecție ce reprezintă un cub centrat în origine cu dimensiunea 2, deci coordonatele X, Y, Z între -1 și +1.
Din spațiul de proiecție este foarte ușor matematic să obținem proiecția finală 2D pe viewport fiind nevoie doar să mapăm informația din cubul [-1,1] scalată corespunzător pe viewport-ul definit de aplicație.
Matricea de proiecție
Trecerea din spațiul de vizualizare în spațiul de proiecție se face tot utilizând o matrice, denumită matrice de proiecție, calculată în funcție de tipul de proiecție definit. Biblioteca GLM oferă funcții de calcul pentru cele mai utilizate 2 metode de proiecție în aplicațiile 3D, anume: proiecția perspectivă și ortografică
Datele (vertecșii din spațiul de vizualizare) sunt înmulțite cu matricea de proiecție pentru a se obține pozițiile corespunzătoare din spațiul de proiecție.
Proiecția ortografică
În proiecția ortografică observatorul este plasat la infinit. Distanța până la geometrie nu influențează proiecția și deci nu se poate determina vizibil din proiecție. Proiecția ortografică păstrează paralelismul liniilor din scenă.
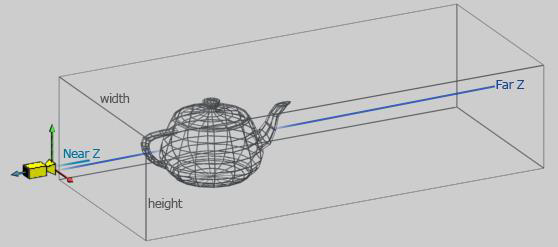
Proiecția ortografică este definită de lățimea și înălțimea ferestrei de vizualizare cât și a distanței de vizualizare dintre planul din apropiere și planul din depărtare. În afara acestui volum obiectele nu vor mai fi văzute pe ecran.
Matricea de proiecție poate fi calculată utilizând funcția glm::ortho unde punctele left, right, bottom, top sunt relative față de centrul ferestrei (0, 0) și definesc înălțimea și lățimea ferestrei de proiecție
glm::mat4 Projection = glm::ortho(float left, float right, float bottom, float top, float zNear, float zFar);
Proiecția perspectivă
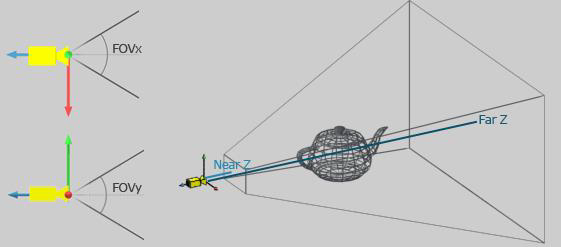
Proiecția perspectivă este reprezentată de un trunchi de piramidă (frustum) definit prin cele 2 planuri, cel din apropiere și cel din depărtare, cât și de deschiderea unghiurilor de vizualizare pe cele 2 axe, OX și OY. În proiecția perspectivă distanța până la un punct din volumul de vizualizare influențează proiecția.
Matricea de proiecție în acest caz poate fi calculată cu ajutorul funcției glm::perspective ce primește ca parametri deschiderea unghiului de vizualizare pe orizontală (Field of View - FoV), raportul dintre lățimea și înălțimea ferestrei de vizualizare (aspect ratio), cât și distanța până la cele 2 planuri zFar și zNear.
glm::mat4 Projection = glm::perspective(float fov, float aspect, float zNear, float zFar);
În cazul proiecției perspectivă, după înmuțirea coordonatelor din spațiul view, componenta w a fiecărui vertex este diferită, ceea ce înseamnă că spațiul de proiecție nu e același pentru fiecare vertex. Pentru a aduce toți vectorii în același spațiu se împarte fiecare componentă a vectorului rezultat cu componenta w. Această operație este realizată automat de procesorul grafic, în cadrul unei aplicații fiind nevoie doar de înmulțirea cu matricea de proiecție.
Volum de vizualizare perspectivă (stânga) și rezultatul obținut (dreapta) în urma aplicării transformării de proiecție asupra geometriei din scenă
Spațiul coordonatelor de dispozitiv normalizate (NDC)
După aplicarea transformărilor de Modelare, Vizualizare și Proiecție iar apoi divizarea cu W a vectorilor, se obține spațiul de coordonate normalizate (NDC) reprezentat de un CUB centrat în origine (0, 0, 0) cu latura 2. Informația din acest cub se poate proiecta foarte ușor pe orice suprafață 2D de desenare definită de utilizator.
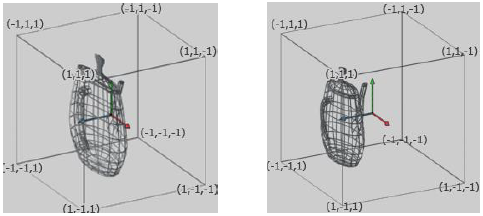
Exemplu rezultat al proiecției în coordonate dispozitiv normalizate (NDC). Proiecție ortografică (stânga), perspectivă (dreapta)
Exemplu vizualizare spațiu NDC din direcția camerei (stânga) și proiecția corespunzătoare pentru un anumit viewport (dreapta)
Aplicarea Transformărilor de Modelare, Vizualizare și Proiecție
Aplicarea trasformărilor de Modelare, Vizualizare și Proiecție se face prin înmulțirea fiecărui vertex al geometriei din scenă cu cele 3 matrici calculate.
pos_vertex = Projection * View * Model * pos_vertex
RenderMesh. Înmulțirile respective sunt executate pe procesorul grafic în cadrul programului vertex shader ce va fi introdus începând cu laboratorul următor.
Transformări de Cameră
Implementarea unei camere în cadrul unei aplicații 3D depinde de cerințele aplicației. În practică cele mai utilizate tipuri de implementări de cameră sunt: First person și Third person.
First-person Camera
Camera de tipul First-person presupune faptul că scena 3D este vizualizată din perspectiva ochilor unui observator, adesea uman. Constrângerile de implementare sunt următoarele:
Translația camerei First-person
- translațiile față/spate se calculează utilizând vectorul forward (direcția de vizualizare sau proiecția acestuia în planul orizontal XOZ)
- translațiile sus/jos se calculează utilizând vectorul local Up sau cel mai adesea direcția OY globală (
glm::vec3(0, 1, 0)) - translațiile dreapta/stânga se calculează folosind vectorul local right (ce se poate obține și prin operația de cross product între vectorii forward și up) sau folosind proiecția acestuia pe planul orizontal XOZ
posCamera = posCamera + glm::normalize(direction) * distance;
Rotația camerei First-person
- rotațiile se fac păstrând observatorul pe loc și modificând direcția în care privește acesta
- pentru rotația stânga/dreapta, vectorii forward respectiv right se pot calcula prin aplicarea transformării de rotație în jului axei OY globale. Se poate roti și în jurul axei OY locale (vectorul up), însă în general nu prea are aplicabilitate practică
- vectorul up se poate recalcula folosind cross product între right și forward
forward = RotateWorldOY(angle) * forward; right = RotateWorldOY(angle) * right; up = glm::cross(right, forward);
- rotația sus/jos se poate face rotind vectorii forward respectiv up în jurul vectorului axei OX adică vectorul right (right rămâne constant)
forward = RotateLocalOX(angle) * forward; up = glm::cross(right, forward);
glm::rotate
glm::mat4 = glm::rotate(glm::mat4 model, float angle, glm::vec3 rotationAxis);
- primul parametru reprezintă o matrice de modelare asupra căreia aplicăm transformarea specificată. Atunci când nu avem o transformare precedentă se pornește de la matricea identitate
glm::mat4(1.0f)
- rotationAxis este axa față de care rotim. În cazul nostru pentru rotația față de OX este vectorul right, pentru rotația față de OZ este vectorul forward, sau
glm::vec3(0, 1, 0)pentru rotația față de OY global
- întrucât vectorii utilizați sunt
glm::vec3când facem înmulțirea va trebui să construim un vector de 4 componente ca să putem înmulți cu matricea de 4×4. Puteți construi vectorul astfel:
glm::vec3 forward = ... glm::vec4 newVec = glm::vec4(forward, 1.0);
- Dacă vrem să rotim vectorul “forward” în jurul axei OY globale atunci facem astfel:
// get the rotate vec4 vector glm::vec4 newVector = glm::rotate(glm::mat4(1.0f), angle, glm::vec3(0, 1, 0)) * glm::vec4(forward, 1); // extract the vec3 vector and then normalize it forward = glm::normalize(glm::vec3(newVector));
glm::vec3 vector = ... glm::vec3 rezultat = glm::normalize(vector);
Third-person Camera
În cazul camerei de tip Third-person observatorul se mută în jurul unui obiect de interes, ce reprezintă întotdeauna centrul atenției. Deci rotațiile se fac într-un mod diferit
Rotația Camerei Third-person
- se translatează observatorul pe direcția de vizualizare în punctul de interes (target)
- se aplică rotația de tip First-person specifică
- se traslatează observatorul înapoi pe noua direcție de vizualizare cu aceeași distanță
Translația Camerei Third-person
Poziția camerei depinde de poziția punctului de interes. Astfel, mișcarea punctului de interes va determina și translația camerei în mod corespunzător.
Cerințe laborator
- Descarcăți framework-ul de laborator
- Să se implementeze camera de tip First Person (fișierul lab_camera.h)
- Să se implementeze camera de tip Third Person (fișierul lab_camera.h)
- Să se completeze funcțiile de translație ale camerei din
Lab5::OnInputUpdate() - Să se completeze funcțiile de rotație ale camerei din
Lab5::OnMouseMove() - Să se deseneze încă 2 obiecte în scena 3D având rotația/scalarea/translația diferite
- aveți grijă să setați matricea de modelare de fiecare dată înainte de desenare
- utilizați
glm::translate(),glm::rotate()șiglm::scale()pentru a construi o matrice de modelare pentru fiecare obiect
- Schimbare proiecție perspectivă/ortografică
- tasta O face trecerea în proiecție ortografică
- tasta P face trecerea în proiecție perspectivă
- Să se modifice FoV-ul camerei în cazul proiecției persepective
- folosiți 2 taste pentru a modifica pozitiv și negativ FoV-ul
- se va folosi
OnInputUpdate()
- Să se modifice lățimea și/sau înălțimea ferestrei de proiecție în cazul proiecției ortografice
- se va folosi
OnInputUpdate()