Laboratorul 0 - Recapitulare

Circuite combinaționale

Circuitele logice combinaționale aplică funcții logice pe semnalele de intrare pentru a obține semnalele de ieșire. Valorile de ieșire depind doar de valorile de intrare, iar când starea unei intrări se schimbă, acest lucru se reflectă imediat la ieșirile circuitului.

Diagrama bloc pentru un circuit combinațional cu n intrări și m ieșiri

Logica combinațională poate fi reprezentată prin:

diagrame structurale la nivel de porți logice
tabele de adevăr
expresii booleene (funcții logice)

Circuitele combinaționale sunt folosite în procesoare în cadrul componentelor de calcul, iar cele mai des întâlnite sunt:

multiplexoarele și demultiplexoarele
codificatoarele și decodificatoarele
sumatoarele
comparatoarele
memoriile ROM (read-only, nu păstrează stare)

Un exemplu de folosire a sumatoarelor este în cadrul Unităților Aritmetice-Logice (UAL) din interiorul procesoarelor.

Porți logice

Porțile logice reprezintă componentele de bază disponibile în realizarea circuitelor combinaționale. Ele oglindesc operațiile din algebra booleană, algebră care stă la baza teoriei circuitelor combinaționale. În sunt prezentate cele mai întâlnite porți logice împreună cu operația booleană pe care o implementează.

Denumire	Operator	Tabel de adevăr
Inversor (NOT)	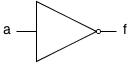f = !a	a		f
		0		1
		1		0
Poarta SAU (OR)	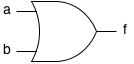f = a \|\| b	a	b	f
		0	0	0
		0	1	1
		1	0	1
		1	1	1
Poarta ŞI (AND)	f = a && b	a	b	f
		0	0	0
		0	1	0
		1	0	0
		1	1	1
Poarta SAU-NU (NOR)	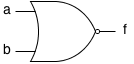f = !(a \|\| b)	a	b	f
		0	0	1
		0	1	0
		1	0	0
		1	1	0
Poarta ŞI-NU (NAND)	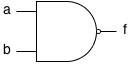f = !(a && b)	a	b	f
		0	0	1
		0	1	1
		1	0	1
		1	1	0
Poarta SAU EXCLUSIV (XOR)	f = a ^ b	a	b	f
		0	0	0
		0	1	1
		1	0	1
		1	1	0
Poarta SAU EXCLUSIV NU (XNOR)	f = !(a ^ b)	a	b	f
		0	0	1
		0	1	0
		1	0	0
		1	1	1

Porțile logice de bază

Sumatorul elementar

Sumatoarele (adders), folosite cel mai mult în unitățile aritmetice logice ale procesoarelor, realizează adunări pe un număr dat de biți, furnizând la ieșirea circuitului suma și transportul (carry) rezultat în urma operației.

Există mai multe tipuri de sumatoare pentru adunarea numerelor pe n biți, iar acestea se bazează pe sumatoare simple de 1 bit, care pot fi de două tipuri:

sumatorul elementar parțial (Half adder) - însumează doi operanzi pe 1 bit și oferă la ieșire suma acestora și transportul.
sumatorul elementar complet (Full adder) - însumează doi operanzi pe 1 bit și un transport și oferă la ieșire suma acestora și transportul.

Diagrama bloc pentru half adder

Diagrama bloc pentru full adder

Diagrama semnale pentru full adder

Sumatorul elementar parțial

Acest sumator este în continuare descris prin expresiile booleene, tabelul de adevăr și schema logică.

Inputs		Outputs
a	b	sum	c_out
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Tabelul de adevăr pentru half adder

Din tabelul de adevăr se pot deduce următoarele formule:

sum   = a ^  b
c_out = a && b

Conform acestor formule putem exprima circuitul prin porți logice, ca în imaginea de mai jos:

Schema logică pentru half adder

Despre tabele de adevăr și deducerea expresiilor booleene (click aici)

Dintr-un tabel de adevăr, pentru fiecare output se va deduce o funcție/expresie aplicând următoarele reguli:

fiecare rând din tabel pentru care funcția are valoarea 1 va genera un termen
termenii sunt formați din parametrii funcției legați prin ȘI
1. dacă parametrul are valoarea 1 se consideră în formă directă
2. dacă parametrul are valoarea 0 se consideră în formă negată
se aplică SAU între toți termenii deduși

Pentru sumatorului elementar parțial avem:

$ sum\ =\ \bar a\ \cdotp\ b\ +\ a\ \cdotp\ \bar b $

$c_{out}\ =\ a\ \cdotp \ b$

În multe cazuri aceste formule sunt prea complexe, conținând multe operații și necesitând multe porți logice pentru a fi implementate. Pentru a reduce complexitatea formulelor rezultate se poate aplica un procedeu de minimizare, care va reduce dimensiunea termenilor sau chiar îi va elimina. Minimizarea se poate realiza folosind teoremele algebrei booleene sau grafic, prin diagrame Karnaugh.

Sumatorul elementar complet

Inputs			Outputs
a	b	c_in	sum	c_out
0	0	0	0	0
0	1	0	1	0
1	0	0	1	0
1	1	0	0	1
0	0	1	1	0
0	1	1	0	1
1	0	1	0	1
1	1	1	1	1

Tabelul de adevăr pentru full adder

Din tabelul de adevăr se pot deduce următoarele formule:

sum   =   a ^ b  ^  c_in
c_out = ((a ^ b) && c_in) || (a && b)

Conform acestor formule putem exprima circuitul prin porți logice sau putem folosi sumatoare elementare parțiale, ca în imaginea de mai jos:

Schema logică pentru full adder

Codul C pentru full adder

void full_adder(int a, int b, int c_in, // inputs
                int *sum, int *c_out)   // outputs
{
    *sum   =   a ^ b  ^  c_in;
    *c_out = ((a ^ b) && c_in) || (a && b);
}

Multiplexorul 4:1

Un multiplexor digital este un circuit combinațional care implementează o funcție de selecție a uneia dintre intrările sale.

$2^n$ intrări
$n$ intrări de selecție
o ieșire

Diagrama bloc a multiplexorului 4:1

Schema logică a multiplexorului 4:1

Alegerea semnalului de ieșire se face pe baza intrărilor de selecție, care reprezintă în baza 2 numărul intrării ce trebuie selectate. În exemplul din imaginea de mai sus avem schema bloc a unui multiplexor cu 4 intrări, iar acesta are nevoie de două intrări de selecție.

Funcția inversă a multiplexorului este realizată de către circuitele de demultiplexare, care preiau un semnal de intrare și folosesc intrările de selecție pentru a-l transmite pe una din ieșirile posibile.

S2	S1	out
0	0	I1
0	1	I2
1	0	I3
1	1	I4

Selecția intrărilor

Deoarece multiplexorul 4:1 are 6 intrări, tabelul de adevăr devine destul de mare și nu mai este indicat de pornit de la acesta pentru obținerea funcției logice. Din descrierea funcționării circuitului și proprietățile porții AND, putem deduce termenii formulei:

$ f = \bar s_1\ \cdotp\ \bar s_2\ \cdotp\ I_1\ +\ s_1\ \cdotp \bar s_2\ \cdotp\ I_2\ +\ \bar s_1\ \cdotp\ s_2\ \cdotp\ I_3\ +\ s_1\ \cdotp\ s_2\ \cdotp\ I_4 $

Conform formulei se poate realiza circuitul cu porți logice din imaginea de mai sus.

Codul C pentru un multiplexor 4:1

Multiplexor 4:1

void mux41(int s1, int s2,                  // selection inputs
           int i1, int i2, int i3, int i4,  // inputs
           int *out)                        // output
{
    switch((s2 << 1) | s1)
    {
        case 0:
            *out = i1;
            break;
 
        case 1:
            *out = i2;
            break;
 
        case 2:
            *out = i3;
            break;
 
        case 3:
            *out = i4;
            break;
    }
}

Sumatorul cu transport succesiv

Cel mai intuitiv mod de a forma un sumator este de a lega în cascadă mai multe sumatoare elementare complete pe 1 bit. În acest fel se formează un sumator cu transport succesiv (eng. ripple-carry adder), cum este cel pe 4 biți din imaginea de mai jos, care primește la intrare a[3:0], b[3:0], c_in și are ca ieșiri suma s[3:0] și transportul c_out. În cazul sumatoarelor pe mai mulți biți nu mai este indicat de pornit întâi de la o tabelă de adevăr deoarece aceasta ajunge la dimensiuni prea mari.

Schema sumatorului cu transport succesiv, pe 4 biți

Un alt avantaj al acestui design simplu, este că se pot forma sumatoare pe mai mulți biți din înlănțuirea oricâtor sumatoare. De exemplu, pentru a însuma numere pe 16 biți se poate crea un sumator ripple-carry din legarea în cascadă a 4 sumatoare pe 4 biți, ca în imaginea de mai jos.

Schema sumatorului cu transport succesiv, pe 16 biți

Deși are un design simplu, dezavantajul acestui sumator este că este lent, fiecare sumator elementar necesitând transportul de la sumatorul precedent. Există alte sumatoare, cum ar fi cel cu transport anticipat (eng. carry-lookahead adder), care oferă o funcționare mai rapidă, eliminând așteptarea propagării transportului.

Circuite secvențiale

Spre deosebire de circuitele logice combinaționale, cele secvențiale (eng: sequential logic) nu mai depind exclusiv de valoarea curentă a intrărilor, ci și de stările anterioare ale circuitului.

Logica secvențială poate fi de două tipuri: sincronă și asincronă. În primul caz, cel cu care vom lucra și la laborator, este folosit un semnal de ceas care comandă elementul/elementele de memorare, acestea schimbându-și starea doar la impulsurile de ceas. În al doilea caz, ieșirile se modifică atunci când se modifică și intrările, neexistând un semnal de ceas pentru elementele de memorare. Circuitele secvențiale asincrone sunt mai greu de proiectat deoarece pot apărea probleme de sincronizare. Din această cauză ele sunt folosite mai rar.

În continuare ne vom referi doar la circuitele secvențiale sincrone.

Schema bloc a unui circuit secvențial sincron

Bistabilul D

Elementele de memorare din circuitele secvențiale pot fi implementate prin bistabile (eng. flip-flops). Acestea stochează valori în funcție de valoarea de la intrare și de semnalul de ceas. Valoarea stocată poate fi schimbată doar atunci când ceasul realizează o tranziție activă (un semnal de ceas poate fi “activ” pe front crescător (eng. rising edge) sau pe front descrescător (eng. falling edge)).

Există 4 tipuri principale de bistabile: D, T, SR și JK, iar în acest laborator ne vom axa pe bistabilul D. Acesta are un design simplu și este folosit în general pentru implementarea registrelor din procesoare (cea mai mică și mai rapidă unitate de stocare din ierarhia de memorie).

Diagrama bloc pentru bistabilul D

Intrările și ieșirile circuitului sunt:

D - valoarea (data) de stocat
clk - semnalul de ceas, considerat activ pe front crescător în descrierile următoare
Q - starea curentă
!Q - starea curentă negată

Ca mod de funcționare, ecuația caracteristică a sa este Qnext = D, adică starea următoare (Qnext) a bistabilului depinde doar de intrarea D, fiind independentă de starea curentă (Q), după cum se observă și din tabelul de mai jos.

D	Q	Qnext
0	0	0
0	1	0
1	0	1
1	1	1

Tabelul de tranziții pentru bistabilul D

Pentru a înțelege mai ușor comportamentul bistabilelor, pe lângă tabelele de tranziții mai sunt utile și diagramele de semnale (eng. timing diagrams), cum este cea din figura de mai jos, unde se poate observa cum ieșirea Q se schimbă doar pe frontul crescător de ceas și devine egală cu intrarea D în momentul tranziției ceasului.

Diagrama de semnale pentru bistabilul D

Automate finite

Prin automate finite (eng. Finite-state machine - FSM) înțelegem de fapt un circuit secvențial sincron așa cum a fost el descris anterior. De obicei, proiectarea unui automat finit pornește de la o descriere informală a modului în care automatul trebuie să funcționeze. Primul pas în realizarea automatului este descrierea formală a funcționării acestuia. Două dintre metodele prin care un automat finit poate fi descris sistematic sunt:

Diagrama de stări prezintă într-un mod grafic funcționarea unui automat finit. Stările automatului sunt reprezentate prin noduri, iar tranzițiile sunt reprezentate prin arce între starea sursă și starea destinație. Fiecare arc este marcat cu condiția necesară pentru a fi efectuată o tranziție. De asemenea, eventualele semnale de ieșire ale automatului sunt marcate în dreptul stărilor care generează acele ieșiri.

Exemplu de diagramă de stări

Starea curentă	x	Starea următoare
S0	1	S1
S1	0	S0

Exemplu de tabel de tranziții

Tabelul de tranziții prezintă funcționarea unui automat finit sub formă de tabel. Fiecare rând al tabelului reprezintă o tranziție a automatului și conține starea curentă, starea următoare și intrările necesare pentru a activa tranziția.

În continuare vom proiecta două automate finite simple:

Recunoaşterea secvenței "ba"

Se dorește proiectarea unui automat finit capabil să recunoască secvența “ba”. Automatul primește la intrare în mod continuu caractere codificate printr-un semnal de un bit (caracterele posibile sunt “a” și “b”). Ieșirea automatului va consta dintr-un semnal care va fi activat (valoarea 1) atunci când ultimele două caractere introduse vor fi “b” urmat de “a”. Semnalul de ieșire va rămâne activ până la introducerea unui nou caracter, după care automatul va continua operația de recunoaștere.

Click pentru rezolvare

Vom începe proiectarea automatului prin identificarea intrărilor și ieșirilor. Din descriere observăm că intrarea este formată dintr-un singur semnal de 1 bit (automatul va avea și o intrare de ceas, însă aceasta nu este considerată intrare propriu zisă de date). Deoarece codificarea caracterelor nu este specificată vom presupune că valoarea 0 indică un caracter “a”, iar valoarea 1 indică un caracter “b”. Ieșirea este formată deasemenea dintr-un semnal de 1 bit cu valoarea 1 atunci când secvența căutată a fost găsită și 0 în rest.

Vom realiza în continuare diagrama de stări a automatului. La pornire, vom inițializa automatul într-o stare pe care o vom numi S0. Dacă la prima tranziție de ceas intrarea are valoarea:

0 (caracterul “a”) - vom avansa într-o stare pe care o vom numi Sa care ne spune că intrarea precedentă a fost “a”
1 (caracterul “b”) - vom avansa într-o stare pe care o vom numi Sb care ne spune că intrarea precedentă a fost “b”

În continuare vom analiza ce se întâmplă atunci când automatul este în starea Sa. Dacă la intrare avem valoarea:

0 (caracterul “a”) - automatul va rămâne în acestă stare, care ne spune că intrarea precedentă a fost “a”
1 (caracterul “b”) - automatul va trece în Sb, care ne spune că intrarea precedentă a fost “b”

Dacă ne aflăm în starea Sb și automatul primește la intrare valoarea:

0 (caracterul “a”) - automatul a întâlnit secvența dorită “ba” (fiind în starea Sb intrarea precedentă a fost “b”, iar intrarea curentă este “a”); vom avansa într-o stare pe care o vom numi SA în care vom activa ieșirea automatului; de asemenea, această stare ne spune și că intrarea precedentă a fost “a”, lucru folosit pentru a putea recunoaște și următoarele secvențe “ba” care vor mai fi întâlnite la intrare
1 (caracterul “b”) - automatul va rămâne în această stare, care ne spune că intrarea precedentă a fost “b”

Dacă ne aflăm în starea SA și automatul primește la intrare valoarea:

0 (caracterul “a”) - automatul va trece în starea Sa care ne spune că intrarea precedentă a fost “a”, însă nu vom activa ieșirea automatului deoarece automatul nu a văzut și caracterul “b”
1 (caracterul “b”) - automatul va trece în starea Sb care ne spune că intrarea precedentă a fost “b”

În momentul de față comportamentul automatului a fost descris complet, toate cele 4 stări identificate având definite tranzițiile pentru toate combinațiile semnalelor de intrare. Figura de mai jos prezintă diagrama de stări a automatului.

Automatul de recunoaștere a secvenței "ba"

O dată determinată diagrama de stări a automatului, putem trece la implementarea acestuia într-un limbaj cunoscut (C/C++/C#/Java):

Automatul de recunoaștere a secvenței "ba"

void FSM_ba(int in,     // FSM input: 0 - a, 1 - b
            int out) {  // FSM output: 0 - not found, 1 - found
 
int state = 0;          // FSM state: 0 - S0, 1 - Sa, 2 - Sb, 3 - SA
 
while(1) {
    switch(state) {
        case 0:
            out = 0;
            break;
 
        case 1:
            out = 0;
            break;
 
        case 2:
            out = 0;
            break;
 
        case 3:
            out = 1;
            break:
    }
 
    read_inputs();
 
    switch(state) {
        case 0:
            if(in == 0)
                state = 1;
            else
                state = 2;
            break;
 
        case 1:
            if(in == 0)
                state = 1;
            else
                state = 2;
            break;
 
        case 2:
            if(in == 0)
                state = 3;
            else
                state = 2;
            break;
 
        case 3:
            if(in == 0)
                state = 1;
            else
                state = 2:
            break:
    }
}

Intersecție semaforizată

Se dorește modelarea prin intermediul unui automat de stări a unei intersecții semaforizate în care mașinile pot intra din nord (N), est (E), sud(S) sau vest (W). Semaforul din nord este sincronizat cu semaforul din sud, iar cel din est este sincronizat cu cel din vest. Duratele de timp pentru cele două direcții vor fi: Nord - Sud: roșu - 40 sec, galben - 10sec, verde - 50sec; Est-Vest: roșu - 60 sec, galben - 10 sec, verde - 30 sec.

Click pentru rezolvare

Vom începe proiectarea automatului prin identificarea intrărilor și ieșirilor. Deoarece descrierea informală nu conține informații despre intrările și ieșirile necesare vom folosi oricâte intrări și ieșiri avem nevoie pentru implementarea comportamentului. Un minim de ieșiri pentru automat reprezintă semnalele de comandă pentru culorile semaforului pentru pietoni și pentru mașini. Cele 5 semnale vor fi:

N_rosu- aprindere culoare roșie pentru mașinile din Nord
N_galben - aprindere culoare galbenă pentru mașinile din Nord
N_verde - aprindere culoare verde pentru mașinile din Nord
E_rosu- aprindere culoare roșie pentru mașinile din Est
E_galben - aprindere culoare galbenă pentru mașinile din Est
E_verde - aprindere culoare verde pentru mașinile din Est
S_rosu- aprindere culoare roșie pentru mașinile din Sud
S_galben - aprindere culoare galbenă pentru mașinile din Sud
S_verde - aprindere culoare verde pentru mașinile din Sud
W_rosu- aprindere culoare roșie pentru mașinile din Vest
W_galben - aprindere culoare galbenă pentru mașinile din Vest
W_verde - aprindere culoare verde pentru mașinile din Vest

Pentru a măsura duratele de timp am putea folosi semnalul de ceas al automatului, introducând multiple stări cu tranziții necondiționate, în care o culoare a semaforului este ținută aprinsă. Având în vedere însă că semnalul de ceas pentru un automat are o perioadă de ceas mică (<< 1 sec) am avea nevoie de multe stări pentru a realiza o durată de 30 sec. O soluție mult mai bună este să folosim un numărător pentru a realiza întârzierile necesare. Numărătorul este un circuit secvențial (automat finit) care poate număra crescător sau descrescător tranzițiile unui semnal, având un semnal de ieșire care este activat atunci când indexul ajunge la 0 sau la o valoare care poate fi controlată. Concret, pentru măsurarea duratelor de timp în automatul nostru vom folosi un numărător crescător a cărui valoare maximă o vom configura pentru a obține duratele de timp necesare, în funcție de perioada de ceas a automatului. Vom adăuga astfel o ieșire (T), care va controla valoarea maximă a numărătorului și o intrare (done) care va primi semnalul de terminare de la numărător.

Diagrama de stări a automatului va urmări tranziția celor 3 culori ale semaforului pentru mașini: verde → galben → roșu → verde .

Automatul intersecției

Odată determinată diagrama de stări a automatului, putem trece la implementarea acestuia într-un limbaj cunoscut (C/C++/C#/Java):

Automatul trecerii de pietoni

void FSM_intersectie(int done,
                 int T,
                 int N_rosu,
                 int N_galben,
                 int N_verde,
                 int S_rosu,
                 int S_galben,
                 int S_verde,
                 int W_rosu,
                 int W_galben,
                 int W_verde,
                 int E_rosu,
                 int E_galben,
                 int E_verde) {
 
int state = 0;                  // FSM state: 0 - N/S_verde, 1 - N/S_galben, 2 - N/S_rosu, 3 - E/W_galben
 
while(1) {
    read_inputs();
 
    N_rosu = 0;
    N_galben = 0;
    N_verde = 0;
    S_rosu = 0;
    S_galben = 0;
    S_verde = 0;
    W_rosu = 0;
    W_galben = 0;
    W_verde = 0;
    E_rosu = 0;
    E_galben = 0;
    E_verde = 0;
 
    switch(state) {
        case 0:
            E_rosu = 1;
            W_rosu = 1;
            N_verde = 1;
            S_verde = 1;
            T = 50;
            if(done == 1)
                state = 1;
            else
                state = 0;
            break;
 
        case 1:
            N_galben = 1;
            S_galben = 1;
            E_rosu = 1;
            W_rosu = 1;
            T = 10;
            if(done == 1)
                state = 2;
            else
                state = 1;
            break;
 
        case 2:
            N_rosu = 1;
            S_rosu = 1;
            E_verde = 1;
            W_verde = 1;
            T = 30;
            if(done == 1)
                state = 3;
            else
                state = 2;
            break;
        case 3:
            N_rosu = 1;
            S_rosu = 1;
            E_galben = 1;
            W_galben = 1;
            T = 10;
            if(done == 1)
                state = 0;
            else
                state = 3;
            break;
    }
}

Resurse

PDF laborator

Administrativ

Laboratoare (ACS)

Laboratoare (IE)

Teme

Tutoriale

Resurse

Laboratorul 0 - Recapitulare

ac-is/lab/lab00.txt · Last modified: 2024/03/05 15:53 by alexandru.predescu

Old revisions

Media Manager Back to top

Laboratorul 0 - Recapitulare

Circuite combinaționale

Porți logice

Sumatorul elementar

Sumatorul elementar parțial

Sumatorul elementar complet

Multiplexorul 4:1

Sumatorul cu transport succesiv

Circuite secvențiale

Bistabilul D

Automate finite

Recunoaşterea secvenței "ba"

Intersecție semaforizată

Resurse

Administrativ

Laboratoare (ACS)

Laboratoare (IE)

Teme

Tutoriale

Resurse

Table of Contents