Laborator 11: Flux maxim în rețele de transport
 Bitdefender este un lider recunoscut în domeniul securității IT, care oferă soluții superioare de prevenție, detecție și răspuns la incidente de securitate cibernetică. Milioane de sisteme folosite de oameni, companii și instituții guvernamentale sunt protejate de soluțiile companiei, ceea ce face Bitdefender unul dintre cei mai de încredere experți în combaterea amenințărilor informatice, în protejarea intimității și datelor, a identității digitale și în consolidarea rezilienței la atacuri. Compania a inovat constant în domenii precum antimalware, Internetul Lucrurilor, analiză comportamentală și inteligență artificială, iar tehnologiile Bitdefender sunt licențiate către peste 180 dintre cele mai cunoscute branduri de securitate din lume.
Bitdefender este un lider recunoscut în domeniul securității IT, care oferă soluții superioare de prevenție, detecție și răspuns la incidente de securitate cibernetică. Milioane de sisteme folosite de oameni, companii și instituții guvernamentale sunt protejate de soluțiile companiei, ceea ce face Bitdefender unul dintre cei mai de încredere experți în combaterea amenințărilor informatice, în protejarea intimității și datelor, a identității digitale și în consolidarea rezilienței la atacuri. Compania a inovat constant în domenii precum antimalware, Internetul Lucrurilor, analiză comportamentală și inteligență artificială, iar tehnologiile Bitdefender sunt licențiate către peste 180 dintre cele mai cunoscute branduri de securitate din lume.
Obiective laborator
În acest laborator vom introduce contextul pentru maximum flow problem și vom studia algoritmi care pot rezolva această problemă.
- Prezentarea noțiunii de rețea de transport și a termenilor asociați.
- Prezentarea problemei (diverse variante).
- Prezentarea algoritmilor pentru calcul unui flux maxim într-o rețea de transport.
Maximum flow problem
Vă rugăm să parcugeți Maximum flow problem pentru a vă familiariza cu contextul, problema și notațiile folosite.
Concepte necesare:
- rețea de transport / flow network
- flux / flow
- flux maxim / maximum flow
- capacitate reziduală / residual capacity
- rețea reziduală / residual network
- drum de ameliorare / augmenting path
- capacitate reziduală a unui drum de ameliorare / residual capacity of augmenting path
Algoritmi
Pentru maximum flow problem există mai mulți algoritmi, dintre care amintim:
- Ford–Fulkerson: Este o metodă (nu un algorithm concret), a cărui complexitate este direct proporțională cu valoarea fluxului maxim - $O(m * f_{max})$. [1]
- Edmonds-Karp: Este o implementare concretă / optimizare a metodei anterioare - $O(n * m^2)$. [2]
- Dinic: O optimizare bazată pe construirea progresivă a unui graf folosind BFS. În fiecare etapă se poate afla fluxul în $O(n * m)$, iar în total sunt $n -1$ etape. Complexitate finală $O(n^2 * m)$. [3]
- Preflow-push / push-relabel: Un algoritm care poate fi optimizat pentru a obține complexitate $O(n^3)$ sau $O(n^2 * m)$.
Puteți consulta capitolul Maximum Flow din Introduction to Algorithms [0] pentru mai multe detalii despre acești algoritmi.
În acest laborator vom studia și analiza metoda Ford-Fulkerson, apoi vom implementa algoritmul Edmonds-Karp (care este o optimizare peste Ford-Fulkerson).
Ford-Fulkerson
Algoritmul lui Lester Randolph **Ford** Jr. și Delbert Ray **Fulkerson**, cunoscut ca și algoritmul / metoda Ford-Fulkerson este un algoritm greedy pentru calcularea fluxului maxim într-o rețea de transport.
Atât timp cât în graf încă există drumuri de ameliorare (augmenting paths), înseamnă că mai putem adauga flux in rețea prin acele drumuri. La fiecare pas alegem un drum de ameliorare, prin care adăugăm cantitatea maximă posibilă de flux.
În practică NU vom folosi direct metoda Ford-Fulkerson, ci vom folosi algoritmul Edmonds-Karp, pe care îl vom analiza în secțiunea următoare.
Edmonds-Karp
Algoritmul lui Jack **Edmonds** și Richard M. **Karp**, cunoscut ca și algoritmul Edmonds-Karp reprezintă o implementare concretă a metodei Ford-Fulkerson. Acest algoritm rezolvă problema drumurilor de ameliorare folosind BFS - adică drumul cel mai scurt (ca și număr de arce), pe care se poate merge ținând cont de restricția de capacitate ($f(u, v) \lt c(u, v)$).
Edmonds-Karp - pseudocod
// apply Edmonds-Karp's algorithm for computing maximum flow in network G // // nodes = list of all nodes from G // adj[node] = the adjacency list of node // example: adj[node] = {..., neigh, ...} => edge (node, neigh) // S = source in network G // T = sink in network G // f = flow in network G // c = capacity in network G // // returns: maxFlow (maximum flow in G from S to T) // Edmonds-Karp(G=(nodes, adj), S, T) { // STEP 0: initialize // * flow in network foreach (u in nodes) { foreach(v in nodes) { f[u][v] = 0; } } // * maximum total flow totalFlow = 0; // STEP 1: Start BFS for finding augmenting path(s). while (BFS finds at least one augmenting path in G) { // STEP 2.1: Compute residual capacity of augmenting path. rc = +oo; // residual capacity foreach ((u, v) in path) { rc = min(rc, c[ u ][ v ] - f[ u ][ v ]); } // STEP 2.2: Update flow on path with rc. foreach ((u, v) in path) { f[ u ][ v ] += rc; // Increase on edge (u, v). f[ v ][ u ] -= rc; // Decrease on edge (v, u). } // STEP 2.3: Update total flow. totalFlow += rc; } return totalFlow; } // Usage example: maxFlow = Edmonds-Karp(G=(nodes, adj), S, T); // Use maxFlow.
Algoritmul Edmons-Karp pornește o parcurgere BFS la fiecare pas. Pentru un drum de ameliorare găsit, calculează capacitatea reziduală a acestuia, apoi crește corespunzător fluxul pe acesta.
La fiecare pas, atunci când se crește fluxul pe un arc, se scade fluxul pe arcul invers (vom demonstra într-o subsecțiune viitoare necesitatea acestui pas pentru corectitudinea algoritmului).
Algoritmul se oprește când nu mai există drumuri de ameliorare. Fluxul pompat până atunci în rețea este maxim.
Exemple
Edmonds-Karp: exemplu rezultat
Fluxul maxim calculat cu Edmonds-Karp pentru rețeaua atașată este: 2.
Drumurile de ameliorare folosite sunt:
- $1 - 2 - 4 - 6$ (capacitate reziduală +1)
- $1 - 3 - 5 - 6$ (capacitate reziduală +1)
Exemplu Edmonds-Karp: exemplu simplu pas cu pas
În această secțiune vom exemplifica de ce doar simpla incrementare a fluxului pe arcele directe nu este suficientă pentru a găsi fluxul maxim în rețea. Următoarea secțiunea conține soluția.
Exemplu Edmonds-Karp: exemplu detaliat cu flux pe arce inverse
În această secțiune vom arăta ce face algoritmul pas cu pas și vom observa necesitatea și corectitudinea scăderii fluxului pe arcele inverse.
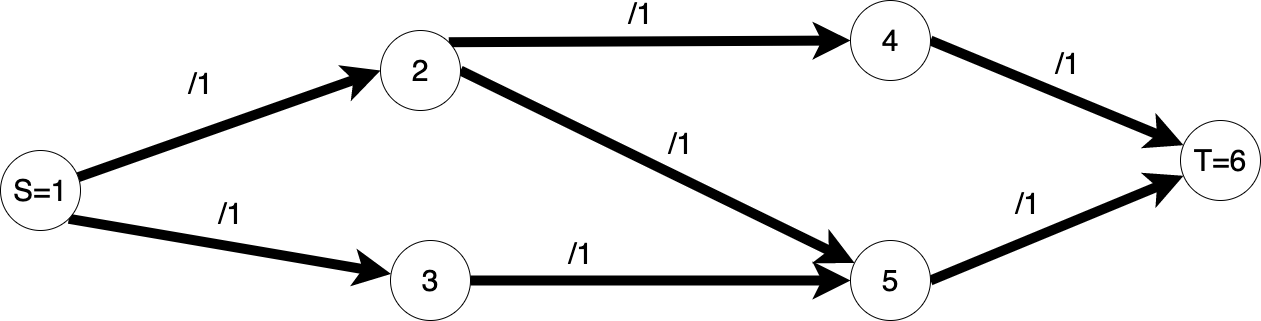
Pornim de la rețeaua din figura următoare:
n = 6,m = 7- Sursa este
S = 1, iar terminalul esteT = 6. - Funcția de capacitate
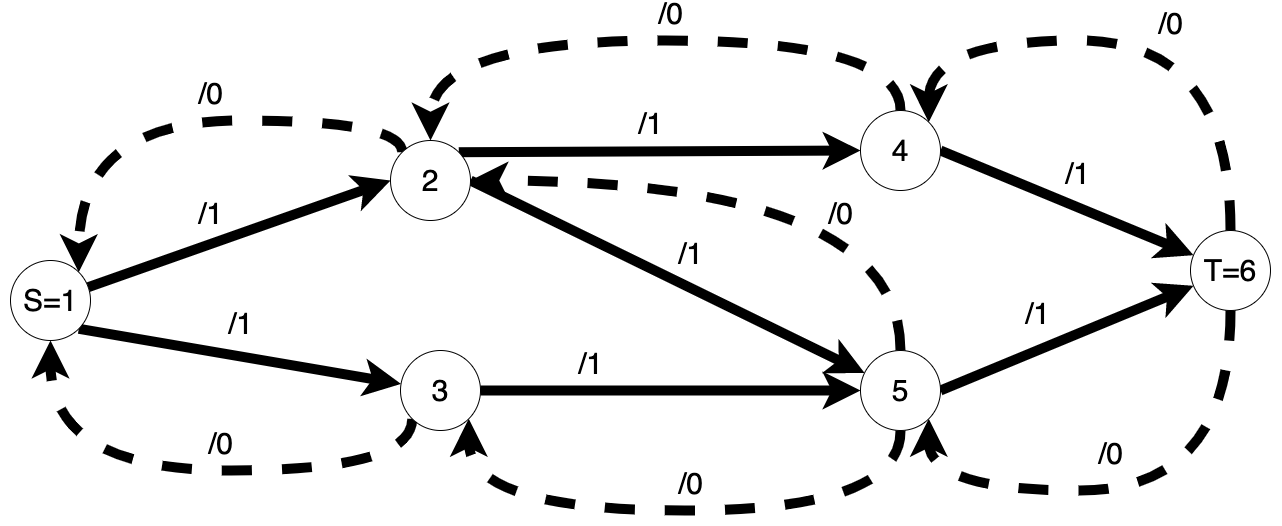
care valorile din figură. - Observăm că pentru fiecare arc $(u, v)$ am dus un arc imaginar $(v, u)$ de capacitate 0. Aceste arce fictive reprezintă cheia funcționării algoritmului Edmonds-Karp: de fiecare dată când vom pompa (adăuga) flux pe un arc $(u, v)$, vom scădea cu aceeași valoare fluxul pe arcul $(v, u)$.
Să vedem în continuare la ce ne ajută dacă alegem din nou, ghinionist, drumul de amelioarare $1 - 2 - 5 - 6$ și dacă de data aceasta putem corecta. Vom face acțiunile marcate în figura următoare:
- Se pompează o unitate de flux pe drumul $1 - 2 - 5 - 6$. Prin urmare pe arcele marcate cu verde creștem fluxul cu +1 unități de flux, iar pe arcele marcate cu roșu scădem (-1 unități de flux).
- La pasul următor, se pornește BFS din 1 și se înaintează folosind aceeași condiție - se poate merge pe o muchie $(u, v)$ dacă $f(u, v) \lt c(u, v)$. De data aceasta, această condiție se îndeplinește și pentru unele dintre muchiile inverse - cele cu -1/0.
Vom face acțiunile marcate în figura următoare:
- Drumul de ameliorare găsit este $1 - 3 - 5 - 2 - 4 - 6$, care are capacitatea reziduală 1. Se pompează +1 pe acest drum (arcele cu verde), se scade în sens invers (arcele cu roșu).
- La următoarea incercare de apelare BFS, nu se mai poate ajunge de la S la T, prin urmare algoritmul se oprește!
- Fluxul găsit este 1 + 1 = 2, care este maxim!
Să observăm că starea finală a rețelei conține 2 unități de flux. Dacă ne uităm cu atenție, observăm că avem o unitate de flux pe drumul $1 - 2 - 4 - 6$ și alta pe $1 - 3 - 5 - 6$.
Deși Edmonds-Karp nu a ales inițial aceste 2 drumuri, s-a corectat pe parcurs, iar în final, dacă fluxul maxim trebuia să treacă pe aici, rețeaua reziduală a fost actualizată / corectată până s-a întâmplat acest lucru!
Semnificația înaintării pe un arc fictiv este că defapt cautăm să deviem fluxul de pe un drum ales anterior (de exemplu, $1 - 2 - 5 - 6$), pe o altă cale (de exemplu, porțiunea $1 - 2$ să se continue cu $2 - 4 - 6$), astfel încât să putem folosi partea eliberată (de exemplu, $5 - 6$), în construcția unui nou drum la pasul curent.
Complexitate
- complexitate temporală: $T = O(n * m^2)\ sau\ O(|V| * |E|^2)$
- complexitate spațială : $S = O(n)\ sau \ O(|V|)$
TLDR
- Ford-Fulkerson este un tipar general, în practică vom folosi doar algoritmul Edmonds-Karp.
- Algoritmul de bazează pe pomparea fluxului pe arcele directe și scăderea pe arcele inverse.
- Ordinea în care drumurile de amelioare sunt găsite nu contează. Este un algoritm greedy de tip constructiv care își corectează deciziile pe parcurs. În final mereu găsește fluxul maxim!
- Dacă în plus avem și costuri pe arce, putem determina flux maxim de cost minim cu Edmonds-Karp înlocuind BFS cu Dijkstra pentru găsirea drumurilor de ameliorare.
Exerciții
Scheletul de laborator se găsește pe pagina pa-lab::skel/lab12.
Înainte de a rezolva exercițiile, asigurați-vă că ați citit și înțeles toate precizările din secțiunea Precizari laboratoare 07-12.
Prin citirea acestor precizări vă asigurați că:
- știți convențiile folosite
- evitați buguri
- evitați depunctări la lab/teme/test
Edmonds-Karp
Se dă un graf orientat cu n noduri și m arce. Graful are pe arce capacitati pozitive.
Folosiși Edmonds-Karp pentru a găsi fluxul maxim între nodul sursă 1 și nodul destinație n în graful dat.
Restricții și precizări:
- $ n <= 10^3 $
- $ m <= 5 * 10^3 $
- $ 1 <= c <= 110.000$, unde c este capacitatea unui arc
- Nu există arce de la n la 1.
- timp de execuție
- C++:
1s - Java:
2s
Rezultatul se va returna sub forma unui singur număr, reprezentând fluxul maxim ce poate fi trimis prin rețea.
BONUS
La acest laborator, asistentul va alege 1-2 probleme din secțiunea extra.
Extra
Referințe
[0] Chapter Maximum Flow, “Introduction to Algorithms”, Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest and Clifford Stein.
[1] Maximal flow through a network, L.R. Ford, D.R. Fulkerson
[2] Theoretical improvements in algorithmic efficiency for network flow problems, Edmonds, Jack; Karp, Richard M.
[3] Dinitz Algorithm, Yefim Dinitz