Laborator 07: Parcurgerea grafurilor. Aplicații (2/2)

• Înțelegerea conceptelor de graf, reprezentare și parcugere
• Studierea unor aplicații pentru parcurgeri

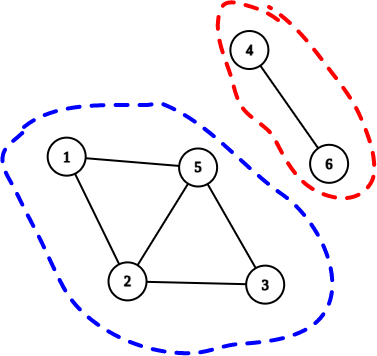
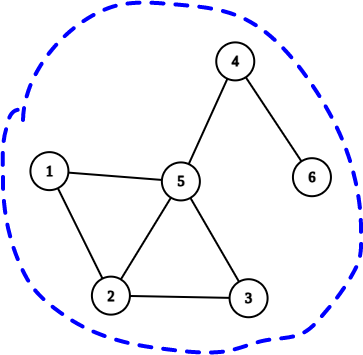
O componentă conexă (CC) / Connected Component (CC) într-un graf neorientat este o submulțime maximală de noduri, cu proprietatea că oricare ar fi două noduri x și y din aceasta, există drum de la x la y.

Un graf neorientat este conex dacă conține o singură componentă conexă.

$T = O(n + m)$

$T = O(n + m)$

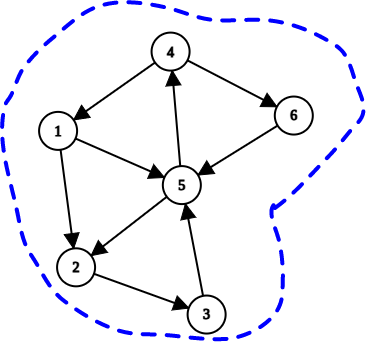
O componentă tare conexă (CTC) / Strongly Connected Component (SCC) într-un graf orientat este o submulțime maximală de noduri, cu proprietatea că oricare ar fi două noduri x și y din aceasta, există drum de la x la y.

Un graf orientat este tare conex dacă conține o singură componentă tare conexă.

Algoritmul lui Tarjan pentru SCC foloseşte o singură parcurgere DFS în urma căreia rezultă o pădure de arbori DFS. Componentele tare conexe vor fi subarbori în această pădure. Rădăcinile acestor subarbori se vor numi rădăcinile componentelor tare conexe (SCC roots).

Nodurile sunt puse pe o stivă, în ordinea vizitării. Când parcurgerea termină de vizitat un subarbore, se determină dacă rădăcina arborelui care s-a terminat de vizitat este și rădăcina unui SCC. Dacă un nod este rădăcina unei componente, atunci el şi toate de deasupra sa din stivă formează acea componentă tare conexă.

Pentru a determina dacă un nod este rădăcina unei componente tare conexe, se definesc:

// the timestamp when node was found (when started to visit its subtree)
found[node] = start[node];
 
// the minimum accessible timestamp that node can see/access
low_link[node] =  min { found[x] | x is node OR x in ancestors(node) OR x in descendants(node) };

Tarjan SCC: node is root for a SCC if low_link[node] == found[node].

| TARJAN_SCC

// Tarjan_SCC
// * visit all nodes with DFS
//      * compute found[node] and low_link[node]
//      * extract SCCs
//
// nodes     = list of all nodes from G
// adj[node] = the adjacency list of node
//             example: adj[node] = {..., neigh, ...} => edge (node, neigh)
TARJAN_SCC(G = (nodes, adj)) {
    // STEP 1: initialize results
    // parent[node] = parent of node in the DFS traversal
    //
    // the timestamp when node was found (when started to visit its subtree)
    // Note: The global timestamp is incremented everytime a node is found.
    //
    // the minimum accessible timestamp that node can see/access
    // low_link[node] =  min { found[x] | x is node OR x in ancestors(node) OR x in descendants(node) };
    //
    foreach (node in nodes) {
        parent[node] = null; // parent not yet found
        found[node] = +oo; // node not yet found
        low_link[node] = +oo; // value not yet computed
    }
    nodes_stack = {}; // visiting order stack
 
    // STEP 2: visit all nodes
    timestamp = 0; // global timestamp
    foreach (node in nodes) {
        if (parent[node] == null) { // node not visited
            parent[node] = node; // convention: the parent of the root is actually the root
 
            // STEP 3: start a new DFS traversal this subtree
            DFS(node, adj, parent, timestamp, found, low_link, nodes_stack);
        }
    }
}
 
DFS(node, adj, parent, ref timestamp, found, low_link, nodes_stack) {
    // STEP 1: a new node is visited - increment the timestamp
    found[node] = ++timestamp; // the timestamp when node was found
    low_link[node] = found[node]; // node only knows its timestamp
    nodes_stack.push(node); // add node to the visiting stack
 
    // STEP 2: visit each neighbour
    foreach (neigh in adj[node]) {
        // STEP 3: check if neigh is already visited
        if (parent[neigh] != null) {
            // STEP 3.1: update low_link[node] with information gained through neigh
            // note: neigh is in the same SCC with node only if it's in the visiting stack;
            // otherwise, neigh is from other SCC, so it should be ignored
            if (neigh in nodes_stack) {
                low_link[node] = min(low_link[node], found[neigh]);
            }
 
            continue;
        }
 
        // STEP 4: save parent
        parent[neigh] = node;
 
        // STEP 5: recursively visit the child subtree
        DFS(neigh, adj, parent, timestamp, found, low_link, nodes_stack);
 
        // STEP 6: update low_link[node] with information gained through neigh
        low_link[node] = min(low_link[node], low_link[neigh]);
    }
 
    // STEP 7: node is root in a SCC if low_link[node] == found[node]
    // (there is no edge from a descendant to an ancestor)
    if (low_link[node] == found[node]) {
        // STEP 7.1: pop all elements above node from stack => extract the SCC where node is root
        new_scc = {};
        do {
            x = nodes_stack.pop();
            new_scc.push(x);
        } while (x != node); // stop when node was popped from the stack
 
        // STEP 7.2: save / print the new SCC
        print(new_scc);
    }
}

Observații:

• La pasul 3.1 se încearcă actualizarea lui low_link[node] cu informația din neigh doar dacă neigh este în stivă.
  • Nodul neigh are deja părinte, deci poate fi în unul din următoare 2 cazuri:
    • neigh este în curs de vizitare (deci este în stivă) ⇒ neigh este strămoș a lui node
      • Reactualizăm low_link[node] cu valoarea din neigh.
    • neigh este deja vizitat (deci a fost scos din stivă) ⇒ neigh face parte din alt subarbore, terminat anterior.
      • Prin urmare, anterior s-a stabilit că neigh face parte dintr-un alt SCC și trebuie ignorat (întrucât sigur are valoare found mai mică decât a lui node și ar reactualiza low_link[node] în mod eronat.
  • Se face această actualizare doar dacă neigh este strămoș al lui

• complexitate temporală : $T = O(n + m)$
• complexitate spațială : $S = O(n)$
  • recursivitate + câteva structuri de date de lungime $O(n)$

Există și alt algoritm pentru determinarea componentelor tare conexe. Algoritmul lui Kosaraju se bazează pe compactarea ciclurilor. Deoarece are aceeași complexitate ca și Tarjan, nu îl vom studia la laborator la PA. Am ales algoritmul lui Tarjan întrucât îl putem modifica ușor pentru a produce și alte rezultate.

Puteți consulta următoarele materiale dacă doriți să aflați mai multe:

• https://www.youtube.com/watch?v=RpgcYiky7uw
• https://iq.opengenus.org/kosarajus-algorithm-for-strongly-connected-components/

Punct de articulație / nod critic / Cut Vertex (CV) este un nod într-un graf neorientat a cărui eliminare duce la creșterea numărului de componente conexe (CC) - se elimină nodul împreună cu muchiile incidente.

Putem modifica ușor algoritmul TARJAN SCC astfel încât să obținem Algoritmul lui Tarjan pentru CV.

În mod analog, pentru a determina dacă un nod este CV, se definesc și folosesc found și low_link.

TARJAN CV: node is CV if
i) node is NOT root and low_link[neigh] >= found[node] for at least one neigh in adj[node]
OR
ii) node is root and children(node) > 1

Dacă node este rădăcină într-un subarbore, acesta are valoarea found mai mică decât a oricărui nod. Prin urmare, condiția low_link[neigh] >= found[node] ar fi adevărată mereu și nu ne-ar putea furniza o informație utilă. De aceea, cazul i) nu este aplicabil pentru rădăcină. Putem trata foarte simplu cazul pentru rădăcină folosind ii): dacă node este rădăcină a unui subarborele și are cel puțin 2 copii, atunci, prin eliminarea lui node, arborele acestuia se sparge într-un număr de subarbori egal cu numărul de copii.

Punem la dispoziție un diff de pseudocod: TARJAN_SCC vs TARJAN_CV. Se observă că este același algoritm, singurele diferențe relevante sunt:

• STEP 3.1: condiția după care se reactulizează low_link[node] în funcție de neigh atunci când cel din urmă este deja vizitat
• STEP 7: condiția prin care se determină dacă node este o rădăcină de SCC / CV.

• complexitate temporală : $T = O(n + m)$
• complexitate spațială : $S = O(n)$
  • recursivitate + câteva tablouri auxiliare de lungime n

Punte / muchie critică / Critical Edge (CE) este o muchie într-un graf neorientat a cărei eliminare duce la creșterea numărului de componente conexe (CC) - se elimină muchia, fără a se sterge capetele (nodurile) acesteia.

Se modifică algoritmul de CV. Se folosesc aceleași definiții și semnificații pentru found și low_link.

TARJAN CE: (node, neigh) is a CE if low_link[neigh] > found[node] where neigh in adj[node].

• complexitate temporală : $T = O(n + m)$
• complexitate spațială : $S = O(n)$
  • recursivitate + câteva structuri de date de lungime $O(n)$

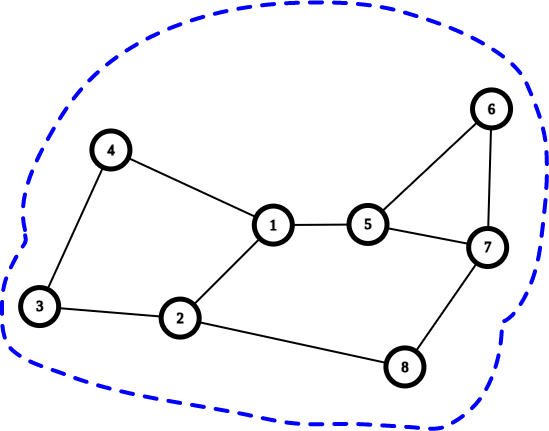
O componentă biconexă / BiConnected Component (BCC) într-un graf neorientat este o submulțime maximală de noduri cu proprietarea că nu conține puncte de articulație - oricare nod s-ar elimina, nodurile rămase sunt încă conectate.

Un graf neorientat este biconex dacă nu conține puncte de articulație - conține o singură componentă biconexă.

Se modifică algoritmul de CV. Se folosesc aceleași definiții și semnificații pentru found și low_link.

• Se folosește o stivă edges_stack în care se adaugă toate muchiile (node, neigh) atunci când se înaintează în recursivitate.
• Atunci când se termină de vizitat un copil neigh, dacă se îndeplinește condiția de CV (low_link[neigh] >= found[node]), înseamnă că prin eliminarea lui node tot subarborele node - neigh - … rămâne deconectat. Prin urmare, toate muchiile din stivă de deasupra muchiei (node, neigh) (inclusiv) formează o componentă biconexă (mulțimea de noduri formată din capetele acestor muchii).
• Se termină de vizitat copilul curent și se trece la următorul. De fiecare dată când se găsește un copil neigh cu low_link[neigh] >= found[node] se formează o nouă BCC.

• complexitate temporală : $T = O(n + m)$
• complexitate spațială : $S = O(n + m)$
  • recursivitate + câteva structuri de date de lungime $O(n)$ / $O(m)$
    • ATENȚIE! În plus, față de CE/CV , se stochează o stivă de muchii.

• SCC: Data Mining, Compilatoare, problema 2-SAT.
• BCC: cele mai importante aplicații se găsesc în rețelele de calculatoare, deoarece un BCC asigură redundanţă (există cel puțin 2 căi de a conecta o entitate la celelalte).

• Se poate folosi/modifica algoritmul lui Tarjan pentru a determina SCC, CV / CE / BCC.
• Deoarece algoritmul se folosește de o parcurgere DFS, complexitatea este liniară în toate cazurile.

Se dă un graf orientat cu n noduri și m arce. Să se găsească componentele tare-conexe folosind algoritmul lui Tarjan. Secțiunea de teorie conține exemple grafice explicate.

Se dă un graf neorientat conex cu n noduri și m muchii. Se cere să se găsească toate punctele critice folosind algoritmul lui Tarjan. Secțiunea de teorie conține exemple grafice explicate.

Se dă un graf neorientat conex cu n noduri și m muchii. Se cere să se găsească toate muchiile critice folosind algoritmul lui Tarjan. Secțiunea de teorie conține exemple grafice explicate.

Se dă un graf neorientat conex cu n noduri și m muchii. Se cere să se găsească toate componentele biconexe folosind algoritmul lui Tarjan. Secțiunea de teorie conține exemple grafice explicate.

[0] Chapter Elementary Graph Algorithms, “Introduction to Algorithms”, Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest and Clifford Stein

[1] https://en.wikipedia.org/wiki/Tarjan%27s_strongly_connected_components_algorithm

[2] https://en.wikipedia.org/wiki/Biconnected_component

[3] “Depth-first search and linear graph algorithms”, R.Tarjan

[4] https://en.wikipedia.org/wiki/Kosaraju%27s_algorithm