This is an old revision of the document!
Laborator 10 - Flux Maxim
Obiective laborator
- formalizarea noțiunilor de rețea de transport și flux în rețea
- prezentarea unei metode de rezolvare a problemei de flux maxim
- analiza unei implementări a metodei oferite
Importanţă – aplicaţii practice
Un graf orientat poate fi utilizat pentru modelarea unui proces de transport într-o rețea între un producător s și un consumator t. Destinația nu poate consuma mai mult decât se produce, iar cantitatea trimisă pe o cale nu poate depăși capacitatea sa de transport.
Rețelele de transport pot modela curgerea lichidului în sisteme cu țevi, deplasarea pieselor pe benzi rulante, deplasarea curentului prin rețele electrice, transmiterea informațiilor prin rețele de comunicare etc.
Descrierea problemei şi a rezolvărilor
O problemă des întâlnită într-o rețea de transport este cea a găsirii fluxului maxim posibil prin arcele rețelei astfel încât:
1. să nu fie depășite capacitățile arcelor
2. fluxul să se conserve în drumul său de la s la t
Definiție 1
O rețea de transport este un graf orientat G = (V,E) cu proprietățile:
1. există două noduri speciale în V: s este nodul sursă (sau producătorul) și t este nodul terminal (sau consumatorul).
2. este definită o funcție totală de capacitate c: V×V → R+ astfel încât:
c (u,v) = 0dacă(u,v) ∉ Ec (u,v) ≥ 0daca(u,v) ∈ E
3. pentru orice nod v ∈ V \ {s,t} există cel puțin o cale s —> v —> t.
Definiție 2
Numim flux în rețeaua G = (V,E ) o funcție totală f: V×V → R cu proprietățile:
1. Restricție de capacitate:
f(u,v) ≤ c(u,v), ∀(u,v) ∈ V- fluxul printr-un arc nu poate depăși capacitatea acestuia
2. Antisimetrie:
f(u,v) = -f(v,u) , ∀u ∈ V, ∀v ∈ V
3. Conservarea fluxului:
Σ f(u,v) = 0, ∀u ∈ V ∖ {s,t}, v ∈ V
Un flux negativ de la u la v este unul virtual, el nu reprezintă un transport efectiv, ci doar sugerează că există un transport fizic de la v la u (este o convenție asemănătoare cu cea făcută pentru intensitățile curenților într-o rețea electrică). Ultima proprietate ne spune că la trecerea printr-un nod fluxul se conservă: suma fluxurilor ce intră într-un nod este 0 (ținând cont de convenția de semn stabilită).
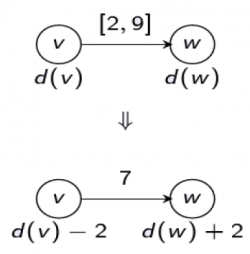
Numim capacitate reziduală a unui arc
cf (u,v) = c(u,v) - f(u,v)
și o interpretăm ca fiind cantitatea de flux adițional care poate fi transportat de la u la v, fără a
depăși capacitatea c(u,v).
Exemplu:
Daca avem arcul (u,v) ∈ V cu c(u,v) = 15 și f(u,v) = 10, se pot transporta cf(u,v) = 5 unități suplimentare fără a încălca restricția de capacitate. Dar, conform definiției, deși arcul (v,u) ∉ V vom avea totuși o capacitate reziduală cf(v,u) = c(v,u) – f(v,u) = 0 − (−10) = 10: as putea transporta 10 unități în sens opus care să le anuleze pe cele 10 ale fluxului direct pe muchia (u,v).
Definiție 3
Fie o rețea de flux G = (V,E), iar f fluxul prin G. Numim rețea reziduală a lui G, indusă de f, o rețea de flux notată cu Gf = (V, Ef), astfel încât
Ef = {(u,v) ∈ V ∣ cf(u,v) = c(u,v) − f(u,v) > 0}
Este important de observat că Ef și E pot fi disjuncte: un arc rezidual (u,v) apare în rețeaua reziduală doar dacă capacitatea sa este strict pozitivă (ceea ce nu implică existența arcului în rețeaua originală).
Un drum de ameliorare este o cale (u1, u2, …, uk), unde u1 = s și uk = t, în graful rezidual cu cf(ui, ui+1) > 0, ∀i=1,2,…,k−1. Practic, un drum de ameliorare va reprezenta o cale în graf prin care se mai poate pompa flux adițional de la sursa la destinație.
Așa cum era de intuit, capacitatea reziduală a unui drum de ameliorare p este cantitatea maximă de flux ce se poate transporta de-a lungul lui:
cf(p) = min{cf(u,v) ∣ (u,v) ∈ p}
Acum că am introdus noțiunile necesare pentru formalizarea problemei de flux maxim într-un graf, putem să prezentăm și cea mai utilizată metodă de rezolvare.
Algoritmul Ford-Fulkerson
Aceasta este o metodă iterativă de găsire a fluxului maxim într-un graf care pleacă de la ideea: cât timp mai există un drum de ameliorare (o cale de la sursă la destinație) pot pompa pe această cale un flux suplimentar egal cu capacitatea reziduală a căii.
Acest algoritm reprezintă mai mult un șablon de rezolvare pentru că nu detaliază modul în care se alege drumul de ameliorare din rețeaua reziduală.
Ford_Fulkerson
Input G(V,E), s, t
Output |fmax|
|fmax| ← 0
f{u,v) ← 0, ∀(u,v) ∈ V×V
while ∃a path p(s ---> t) in Gf such that cf(u,v) > 0, ∀(u,v) ∈ p
find cf(p) = min{cf(u,v) | cf(u,v) ∈ p}
|fmax| += cf(p)
for-each (u,v) ∈ p
f(u,v) ← f(u,v) + cf(p)
f(v,u) ← −f(u,v)
return |fmax|
Complexitatea va fi O(E * f max) pentru că în ciclul while putem găsi, în cel mai rău caz, doar cai care duc la creșterea fluxului cu doar o unitate la fiecare pas.
Ne punem acum problema dacă acest algoritm este corect, dacă la final vom avea cu adevărat fluxul maxim posibil prin graf. Corectitudinea algoritmului derivă imediat din teorema Flux maxim - tăietura minimă.
Numim o tăietură a unui graf o partiție (S,T) a nodurilor sale cu proprietatea s ∈ S si t ∈ T.
Teorema flux maxim – tăietura minimă:
Pentru o rețea de flux G(V,E) următoarele afirmații sunt echivalente:
1. f este fluxul maxim în G
2. Rețeaua reziduală Gf nu conține drumuri de ameliorare
3. Există o tăietură (S,T) a lui G astfel încât fluxul net prin tăietură este egal cu capacitatea acelei tăieturi.
Obs: Prin orice tăietură fluxul este egal cu cel maxim pentru că nu există o altă cale pe care ar putea ajunge flux de la sursă la destinație și care să nu treacă prin tăietură (ar încălca tocmai definiția ei); sau, altfel spus, valoarea unui flux într-o rețea este dată de fluxul oricărei tăieturi. Astfel, fluxul total va fi mărginit de cea mai mică capacitate a unei tăieturi. Dacă este îndeplinit punctul 3. al teoremei atunci știm că acea tăietură nu poate fi decât una de capacitate minimă. Ultima incercare de a gasi o cale de la sursa la drena va rezulta in gasirea doar a elementelor marginite de o astfel de taietura.
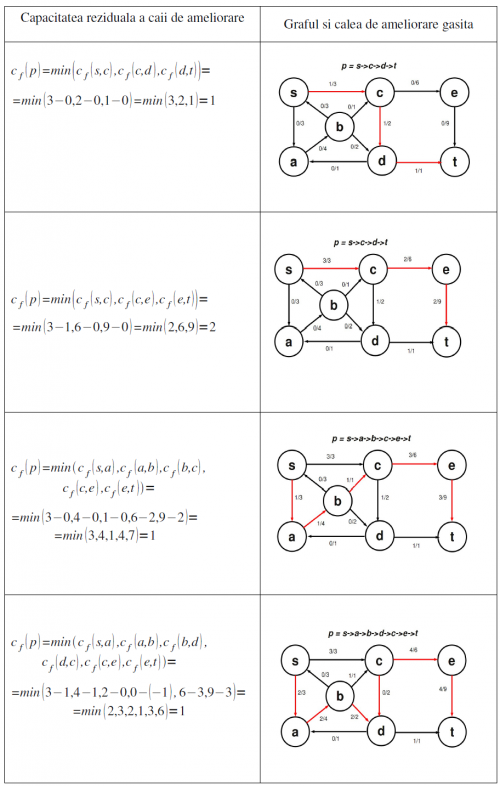
Exemplu:
Observăm că deși muchia (d,c) are capacitate 0 în rețeaua originală (ea nu ar putea transporta flux) în rețeaua reziduală avem c(d,c) = 1 ceea ce îi permite să facă parte din drumul de ameliorare p1 = (s, a, b, d, c, t) de capacitate cf(p1) = 1, astfel că adăugarea acestui flux suplimentar pe muchia (d,c) nu va duce la încălcarea restricției de capacitate; sau am fi putut alege drumul p2=(s, a, c, t) cu cf(p2) = 1 sau p3 = (s,a,b,d,t) cu cf(p3) = 1.
Performanța algoritmului ține de modul în care va fi ales drumul de ameliorare, se poate întâmpla ca pentru |fmax| de valoarea mare o alegere nepotrivită să ducă la timpi de execuție foarte mari.
Implementarea Edmonds-Karp
Așa cum am văzut, algoritmul Ford-Fulkerson nu definește o metodă de alegere a drumului de ameliorare pe baza căruia se modifică fluxul în graf. Implementarea Edmonds-Karp alege întotdeauna cea mai scurtă cale folosind o căutare în lățime în graful rezidual unde fiecare arc are ponderea 1. Se poate demonstra că lungimea căilor găsite astfel crește monoton cu fiecare nouă ameliorare.
Edmonds-Karp Input G(V,E), s, t Output |fmax| |fmax| ← 0 f(u,v) ← 0, ∀(u,v) ∈ V×V while true p(s ⇢ t) ← BFS(Gf,s,t) if not ∃p(s ⇢ t) break; find cf(p) = min{cf(u,v) ∣ cf(u,v) ∈ p} |fmax| += cf(p) for-each (u,v) ∈ p f(u,v) ← f(u,v) + cf(p) f(v,u) ← −f(u,v) return |fmax|
Plecând de la ideea că drumurile de ameliorare găsite au lungimi din ce în ce mai mari se poate arăta că în această implementare fluxul se mărește de cel mult O(V*E) ori ([1], pag.513).
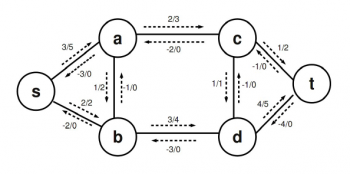
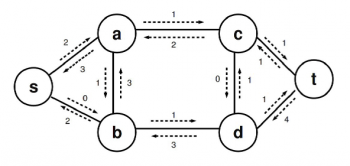
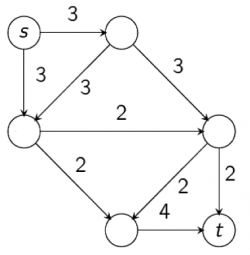
Complexitatea algoritmului va fi O(V*E2). Să luăm un exemplu de rulare al acestui algoritm. Vom considera starea rețelei după ce a fost găsita prima cale de pompare flux(inițial toate arcele sunt etichetate cu 0/0 conform notației stabilite):
Obs: In cazul ultimului drum de ameliorare găsit in exemplul dat, se observa ca deși nu exista muchia (d,c) se simulează un flux pe aceasta printr-unul negativ in sens opus.
Variații ale problemei clasice
In rețelele clasice studiate pana acum aveam o sursa unica care putea produce oricât, destinația unica consuma oricât, orice nod intermediar conserva fluxul, iar singura constrângere a muchiilor era limitarea superioara a fluxului prin capacitate. Sa vedem cum putem generaliza aceste condiții si daca rețelele obținute ar putea fi reduse la una clasica.
Surse si destinații multiple
Se observă ca putem reduce acest graf la cel cunoscut prin adăugarea unei meta-surse legată de sursele mici prin muchii de capacitate nelimitata si analog un meta-terminal cu aceleași proprietăți. Global comportamentul rețelei de flux nu se va schimba.
Cuplaj bipartit maxim
Fiind dat un graf neorientat G = (V,E), un cuplaj este o submultime de muchii M inclusa in E astfel incat pentru toate varfurile v ∈ V, exista cel mult o muchie in M incidenta in v. Spunem ca un varf v ∈ M este cuplat de cuplajul M daca exista o muchie in M incidenta in v. Un cuplaj maxim este un cuplaj de cardinalitate maxima. In cazul grafurilor bipartite, multimea de varfuri poate fi partitionata in V = L U R, unde L si R sunt disjuncte si toate muchiile din E sunt intre L si R. Problema poate fi rezolvata cu ajutorul notiunii de flux, construind reteaua de transport G' = (V',E') pentru graful bipartit G. Vom alege sursa s si destinatia t ca fiind noi varfuri care nu sunt in V si vom construi V' = V U {s,t}. Arcele orientate ale lui G' sunt date de:
E' = { (s, u) : u ∈ L } U { (u, v) : u ∈ L, v ∈ R si (u, v) ∈ E} U { (v, t) : v ∈ R}
Pentru a completa constructia, vom atribui fiecarei muchii din E' capacitatea unitate.
Rețea cu noduri ce nu conservă fluxul
Spre deosebire de s si t care produc/consumă oricât, un nod intermediar ar putea produce sau consuma o cantitate constanta de flux la trecerea prin el. In acest caz vom avea un invariant la nivel de nod care ia forma:
fin − fout = di, undedieste cantitatea produsă suplimentar (> 0) sau solicitată (< 0) de un nod.
Am putea transforma egalitatea in:
(fin + |di|) – fout = 0, dacădi < 0fin − ( fout + |di|) = 0, dacadi > 0
Altfel spus, un nod ce consumă flux poate fi transformat intr-unul ce conservă fluxul și are un in-arc adițional de capacitate |di|, iar unul ce produce flux va avea un out-arc de aceeași capacitate.
La nivelul unei rețele întregi se adaugă un nod sursă cu muchii către toate nodurile ce consumau flux si un nod destinație dinspre toate nodurile ce produceau flux.
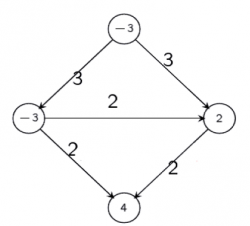
Exemplu:
se va transforma in:
Rețea cu limite inferioare de capacitate
Există cazuri în care aș vrea ca datele de pe muchiile rețelei sa facă parte dintr-un anumit interval [inf, sup]. Pe o astfel de muchie fluxul trebuie să respecte inegalitatea inf ≤ f ≤ sup
Plecând tot de la condițiile de conservare la nivel de nod putem translata intervalul [inf, sup] în [0, sup-inf] și să considerăm că nodul sursă a consumat inf unități de flux iar nodul destinație a produs inf unități. Din exterior entitatea alcătuită din doua noduri și o muchie este văzută ca acționând în același fel asupra fluxului ce o traversează.
Iată un exemplu de transformare:
Bineînțeles că toate aceste transformări pot fi combinate pentru a se ajunge la rețeaua de flux clasică.
Concluzii și observații
Laboratorul de față s-a vrut a fi doar o introducere în domeniul fluxurilor într-un graf – modalitate de a reprezenta probleme de circulație a materialelor atât de frecvent întâlnite. In [1] și [2] găsiți și alți algoritmi interesanți împreună cu studiul complexității lor (algoritmul de pompare preflux, algoritmul „mutare-in-fata”). Spre exemplu, cel mai bun algoritm în prezent pentru cuplajul bipartit maxim se executa in O(√V*E).
Referinte
[1] Introducere in algoritmi, Thomas H. Cormen, Charles E. Leiserson, Ronald R. Rivest – Capitolul VI Algoritmi pe grafuri: Flux maxim
[2] Introducere in analiza algoritmilor, Cristian A. Giumale – Cap. V Algoritmi pr grafuri: Fluxuri maxime intr-un graf
[3] Un articol de la MIT: A Labeling Algorithm for the maximum flow network problem
[4] Resurse wiki – Edmonds Karp Max Flow - Min Cut Theorem
Probleme
Networking (8 pct)
Pornind de la un graf orientat conex și două noduri u și v ale acestuia se cere să se determine următorele elemente:
a) Tăietura minimală a grafului afișată sub forma a unei mulțimi de cardinal minim de muchii ce trebuie eliminate pentru a deconecta u și v. [5 pct]
b) Pentru topologia dată, afișați numărul maxim de drumuri disjuncte între u și v, dar și drumurile în sine. Două drumuri sunt considerate disjuncte dacă nu au nicio muchie în comun [3 pct]
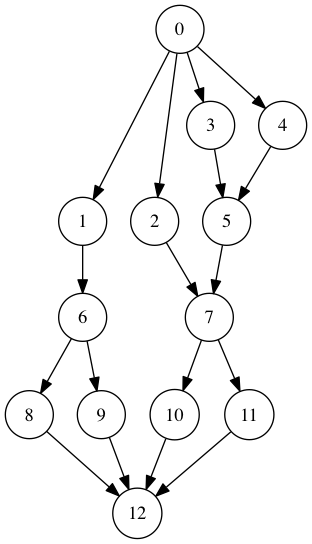
Graful din schelet:
Generare de graf orientat (4 pct)
Se dă o listă de N noduri, pentru fiecare cunoscându-se gradul de intrare si de ieșire al acestora. Realizați un program care să construiască un graf orientat G cu N noduri, care să satisfaca gradele date. Nu se permite mai mult de o muchie între două noduri.
Exemplu:
| Nod | Grad intrare | Grad iesire |
|---|---|---|
| 1 | 1 | 3 |
| 2 | 1 | 2 |
| 3 | 3 | 1 |
| 4 | 2 | 1 |
O soluție posibilă de muchii:
1 2 1 4 1 3 2 3 2 1 3 4 4 3