Laborator 09: Drumuri minime în grafuri: surse / destinații multiple. (2/2) [CS Open CourseWare]

This is an old revision of the document!

# Laborator 09: Drumuri minime în grafuri: sursă / destinație unică. (1/2)

$insert_partnership ## Obiective laborator În laboratorul 9 vom introduce contextul pentru **Shortest-paths problem** și vom studia **Single-source shortest-paths problem**, iar în laboratorul 10 vom continua cu **All-pairs shortest-paths problem**. * Înțelegerea conceptelor de cost asociat unei muchii, relaxare a unei muchii. * Prezentarea problemei drumului de cost minim (diverse variante). * Prezentarea algoritmilor pentru calculul drumurilor minime. ## Shortest-paths problem: single-source/destination Vă rugăm să parcugeți [Shortest-paths problem](https://ocw.cs.pub.ro/courses/pa/laboratoare/shortest-paths-problem) pentru a vă familiariza cu contextul, problema și notațiile folosite. Concepte necesare: * **cost muchie** / **edge cost** * **cost drum** / **path cost** * **problema drumurilor minime: sursă / destinație unică** / **single-source/destination shortest-paths problem** * **relaxarea unei muchii** / **edge relaxation** * **reconstruirea unui drum** / **RebuildPath** ## Algoritmi În acest laborator vom studia **single-source/destination shortest-paths problem**. Pentru această problemă, vom prezenta 2 algoritmi: * **Dijkstra**: presupune ca toate costurile din graf sunt nenegative. * **Bellman-Ford**: permite costuri negative în graf, dar presupune că nu există cicluri de costuri negative. Vom prezenta fiecare algoritm, îl vom analiza, iar la final vom vedea când îl vom folosi pe fiecare. Puteți consulta capitolul **Single-Source Shortest Paths** din **Introduction to Algorithms** [0] pentru mai multe detalii despre acești algoritmi. ## Dijkstra Algoritmul lui [Edsger Wybe **Dijkstra**](https://en.wikipedia.org/wiki/Edsger_W._Dijkstra) (**Dijkstra's algorithm**) rezolvă **shortest-paths problem** în grafuri **G = (V, E)** cu costurile muchiilor **nenegative** ($ w[u][v] \ge 0 $). ### Dijsktra - Pseudocod ```cpp // apply Dijkstra's algorithm from source // // source = the source for the computing distances // nodes = list of all nodes from G // adj[node] = the adjacency list of node // example: adj[node] = {..., neigh, ...} => edge (node, neigh) // // returns: d, p // d = distance vector // p = parent vector // Dijsktra(source, G=(nodes, adj)) { // STEP 0: initialize results // d[node] = distance from source to node // p[node] = parent of node on the shortest path from source to node foreach (node in nodes) { d[node] = +oo; // distance not yet computed p[node] = null; // parent not yet found } // STEP 1: initialize a priority queue pq = {}; // STEP 2: add the source(s) into q d[source] = 0; // distance from source to source p[source] = null; // source never has parent pq.push( (source, d[source]) ); // STEP 3: start relaxation loop using the node(s) from pq while (!pq.empty()) { // STEP 3.1: extract the next node (having the minimum estimate distance) node = pq.pop_min(); // [optional] STEP 3.2: print/use the node // STEP 3.3: relax all edges (node, neigh) foreach (neigh in adj[node]) { if (d[node] + w[node][neigh] < d[neigh]) { // try to relax edge (node, neigh) d[neigh] = d[node] + w[node][neigh]; // update the new distance from source to neigh p[neigh] = node; // save parent pq.push( (neigh, d[neigh]) ); // replace distance for neigh in pq } } } return d, p; } // Usage example: d, p = Dijkstra(source, G=(nodes, edges)); // 1. Use distances from d // (e.g. d[node] = distance from source to node) // // 2. Rebuild path from node to source using parents (p) RebuildPath(source, destination, p); ``` Acest algoritm menține un set de noduri (de exemplu, un min heap / priority queue) cu distanța minimă față de sursă fiind estimată. Cât timp mai există noduri pentru care distanța minimă față de sursă nu este finalizată, se extrage nodul$ node$ pentru care estimarea este minimă și această se consideră finalizată. Deoarece acum distanța de la nodul sursă la $u$ este finală, se relaxează toate muchiile care pornesc din $node$, care sunt de forma $(node, neigh) $. Pentru ca acest algoritm alege mereu "cel mai apropiat nod de sursă" spunem că **Algoritmul lui Dijsktra** este de tip greedy. Demonstrația se poate găsi în **Introduction to algorithms**. ### Exemple #### Exemplu Dijkstra {{https://ocw.cs.pub.ro/courses/_media/pa/new_pa/lab09-graph-dijkstra-example.png?512| Exemplu Dijkstra}} Drumurile minime calculate de algoritmul lui Dijkstra sunt: |node|1|2|3|4|5|6|7|8|9| #newrow |d[node]|0|1|1|3|3|1|3|4|$ +∞ $| #newrow |p[node]|null|1|1|3|4|1|6|5|null| #newrow <spoiler Explicație pas cu pas> În exemplul atașat, avem un graf **orientat** cu următoare configurație: * `n = 9`, `m = 10` * Funcția de cost `w` are valorile menționate pe muchii. * Avem mai multe drumuri de cost diferite între diverse perechi de noduri din graf. * Alegem$ source = 1 $și rulăm pas cu pas algoritmul. * STEP 0: *$ d[node] = +∞$, pentru $node = 1:9$ * $p[node] = null$, pentru $node = 1:9 $* STEP 1: *$ pq = \{\}$ (coadă de priorități în care vom băga elemente $(node, d[node]) $, deci vom ordona nodurilor **crescător după distanța minimă față de sursă** cunoscută în acel moment). * STEP 2: initializări pentru sursă *$ d[1] = 0$ * $p[1] = null$ * $pq.push( (1, 0) ) $(inițial avem în coadă doar sura **1** cu distanța **0**). * STEP 3: scoate câte un nod la fiecare pas și relaxăm toate muchiile care pornesc din acesta; ne oprim când coada e goală. 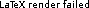*$ pq = \{ (1, 0) \}$ => $pq.{pop\_min}()$ scoate $node = 1 $. Relaxăm muchiile care pornesc din **1**. *$ (1, 2)$: Verificăm dacă $d[1] + w[1][2] < d[2]$ (adică $0 + 1 < +∞ $). **DA**, atunci **relaxarea muchiei are loc**: *$ d[2] = d[1] + w[1][2] = 0 + 1 = 1 $(actualizăm distanța) *$ p[2] = 1 $(actualizăm părintele de pe drum) *$ pq.push( (2, 1) ) $(adăugăm nodul cu noua distanță, pentru a putea fi folosit la un pas ulterior) *$ (1, 3)$: Verificăm dacă $d[1] + w[1][3] < d[3]$ (adică $0 + 1 < +∞ $). DA, atunci relaxarea muchiei are loc: *$ d[3] = 0 + 1 = 1$ * $p[3] = 1$ * $pq.push( (3, 1) )$ * $(1, 6)$: Verificăm dacă $d[1] + w[1][6] < d[6]$ (adică $0 + 1 < +∞ $). DA, atunci relaxarea muchiei are loc: *$ d[6] = 0 + 1 = 1$ * $p[6] = 1$ * $pq.push( (6, 1) )$ * $pq = \{ (2, 1); (3, 1); (6, 1); \}$ => $pq.{pop\_min}()$ scoate $node = 2 $. Relaxăm muchiile care pornesc din **2**. *$ (2, 8)$: Verificăm dacă $d[2] + w[2][8] < d[8]$ (adică $1 + 10 < +∞ $). DA, atunci relaxarea muchiei are loc: *$ d[8] = 1 + 10 = 11$ * $p[8] = 2$ * $pq.push( (8, 11) )$ * $pq = \{ (3, 1); (6, 1); (8, 11); \}$ => $pq.{pop\_min}()$ scoate $node = 3 $. Relaxăm muchiile care pornesc din **3**. *$ (3, 4)$: Verificăm dacă $d[3] + w[3][4] < d[4]$ (adică $1 + 2 < +∞ $). DA, atunci relaxarea muchiei are loc: *$ d[4] = 1 + 2 = 3$ * $p[4] = 3$ * $pq.push( (4, 3) )$ * $pq = \{ (6, 1); (4, 3) (8, 11); \}$ => $pq.{pop\_min}()$ scoate $node = 6 $. Relaxăm muchiile care pornesc din **6**. *$ (6, 7)$: Verificăm dacă $d[6] + w[6][7] < d[7]$ (adică $1 + 2 < +∞ $). DA, atunci relaxarea muchiei are loc: *$ d[7] = 1 + 2 = 3$ * $p[7] = 6$ * $pq.push( (7, 3) )$ * $pq = \{ (4, 3); (7, 3) (8, 11); \}$ => $pq.{pop\_min}()$ scoate $node = 4 $. Relaxăm muchiile care pornesc din **4**. *$ (4, 5)$: Verificăm dacă $d[4] + w[4][5] < d[5]$ (adică $3 + 0 < +∞ $). DA, atunci relaxarea muchiei are loc: *$ d[5] = 3 + 0 = 3$ * $p[5] = 4$ * $pq.push( (5, 3) )$ * $pq = \{ (5, 3); (7, 3) (8, 11); \}$ => $pq.{pop\_min}()$ scoate $node = 5 $. Relaxăm muchiile care pornesc din **5**. *$ (5, 8)$: Verificăm dacă $d[5] + w[5][8] < d[8]$ (adică $3 + 1 < 11 $). DA, atunci relaxarea muchiei are loc: *$ d[8] = 3 + 1 = 4$ * $p[8] = 5$ * $pq.push( (8, 4) ) $(înlocuim nodul 8 din coadă ținînd cont de noua distanță!) *$ pq = \{ (7, 3) (8, 4); \}$ => $pq.{pop\_min}()$ scoate $node = 7 $. Relaxăm muchiile care pornesc din **7**. *$ (7, 8)$: Verificăm dacă $d[7] + w[7][8] < d[8]$ (adică $3 + 2 < 4 $). **NU**, atunci relaxarea muchiei **NU** are loc (nu se trece la următorul pas). *$ pq = \{ (8, 4); \}$ => $pq.{pop\_min}()$ scoate $node = 8 $. Nu există muchii care pornesc din **8**, nu avem ce relaxa la acest pas. *$ pq = \{ \} $=> Coada este goală. STOP! * Drumurile minime sunt finale (cele menționate anterior). Observații: * Distanța minimă față de sursă pentru un nod poate fi recalculată de mai multe ori (de exemplu, nodul **8**). De fiecare dată nodul se reintroduce în coadă (împreună cu noua distanță). Pentru eficiență, înlocuim elementul curent, deoarece are asociată o distanță mai mare și nu ar mai fi folosită. * Mereu se extrage nodul cel mai apropiat de sursă. Distanța asociată cu el în acel moment este finală. În acest exemplu nodurile sunt scoase în ordinea:$ 1, 2, 3, 6, 4, 5, 7, 8 $. * Nodul **9** nu este accesibil, datele pentru el rămân ca la inițializare. </spoiler> #### [Studiu de caz] Exemplu Dijkstra: costuri negative, rezultate eronate Un nod scos din coadă în algoritmul lui Dijkstra are distanță calculată și finală. Ca această abordare greedy să fie corectă, trebuie ca toate costurile din graf să fie **nenegative**. <spoiler Exemplu rezultate eronate aplicare Dijkstra pe graf cu costuri negative> Vom analiza 2 exemple. Pentru simplitate, presupunem ca$ source = 1 $. În figura următoare avem o topologie simplă, pentru care se întâmplă ca algortimul Dijkstra sa producă vectorul de distanțe corect. {{https://ocw.cs.pub.ro/courses/_media/pa/new_pa/lab09-graph-dijkstra-negative-costs-example01.png?512| Dijkstra cu costuri negative - exemplu 01}} Dacă complicăm puțin topologia, de exemplu să adăugăm muchii astfel încât să forțăm actualizarea distanței de la sursă la sursă, obținem următoarea figură: {{https://ocw.cs.pub.ro/courses/_media/pa/new_pa/lab09-graph-dijkstra-negative-costs-example02.png?512| Dijkstra cu costuri negative - exemplu 02}} Când nodul **5** este scos din coadă la un moment dat, acesta va relaxa muschi$ (5, 1)$ (pentru că $d[5] + w[5][1] = 1 - 2 = -1 < d[1]$). Acest lucru duce la $d[1] = -1 $, adică reactualizarea distanței pentru un nod, care anterior a fost scos din coadă, deci distanța calculată era finală. Deci ajunge la o contradicție. </spoiler> ### Complexitate * **complexitate temporală**:$ T = O(m * log n)\ sau\ O(|E| * log |V|) $* **complexitate spațială** :$ S = O(n) $<spoiler Detalii (analiză + optimizări)> * **complexitate temporală**: Se încearcă relaxarea tuturor celor **m** muchii din graf, care poate presupune o inserare în set / coada de priorități -$ O(log n)$, deci $O(m * log n)$ în total pentru relaxări. În plus, se fac $n$ ștergeri, adică $O(n * log n)$, însă acest termen se poate neglija (presupunem că $n « m $). * **complexitate spațială** : Se ține o coadă de priorități / un set cum maximum **n** noduri. * **optimizare**: După cum se poate vedea, complexitatea este dată de numărul de relaxări ($ m $- de care nu putem scăpa, deoarece vrem să relaxăm toate muchiile ca să fim siguri că am găsit drumurile de lungime minimă) și de complexitatea operațiilor de ștergere / căutare / inserare în structura de date de tip priority queue. Putem încerca mai multe tipuri de heapuri - [Heap: Comparison of theoretic bounds for variants](https://en.wikipedia.org/wiki/Heap_(data_structure)#Comparison_of_theoretic_bounds_for_variants). * **Dijkstra cu heap binar** -$ O(m log n) $: Soluția bazată pe un priority queue clasic de mai sus. * **Dijkstra cu heap Fibonacci** -$ O(n logn + m) $: Cea mai rapidă implementare care se poate obține. Exemple în [Fibonacci Heaps and Dijkstra's Algorithm - A Visualization](https://kbaile03.github.io/projects/fibo_dijk/fibo_dijk.html). </spoiler> ## Bellman-Ford Algoritmul Bellman-Ford a fost inițial propus de Alfonso Shimbel (1955), dar publicat (1956-1958) și numit ulterior după [Richard E. **Bellman**](https://en.wikipedia.org/wiki/Richard_E._Bellman) și [Lester Randolph **Ford** Jr. ](https://en.wikipedia.org/wiki/L._R._Ford_Jr.). Acest algoritm rezolvă **shortest-paths problem** în grafuri **G = (V, E)** cu costurile muchiilor oarecare ($ w[u][v] $poate fi și negativ), dar **fără** cicluri de cost negativ (în grafurile de cost negativ nu putem defini costul unui drum care conține un ciclu). Algoritmul **detectează** prezența ciclurilor de costuri negative în graf. 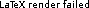Dacă nu există cicluri de cost negativ în graf, acesta furnizează vectorul de distanțe$ d$ și vectorul de părinți $p $(ca și Dijkstra). ### Bellman-Ford - Pseudocod ```cpp // apply Bellman-Ford's algorithm from source // // source = the source for the computing distances // nodes = list of all nodes from G // edges = list of all edges from G // // returns: has_cycle, d, p // has_cycle = negative cycle detection flag (true if found) // d = distance vector (defined only if has_cycle == false) // p = parent vector (defined only if has_cycle == false) // Bellman-Ford(source, G=(nodes, edges)) { // STEP 0: initialize results // d[node] = distance from source to node // p[node] = parent of node on the shortest path from source to node foreach (node in nodes) { d[node] = +oo; // distance not yet computed p(node) = null; // parent not yet found } // STEP 1: set distance and parent for source node d[source] = 0; // distance from source to source p[source] = null; // source never has parent // STEP 2: do |nodes| - 1 relaxations for all edges in G for (i = 1 : |nodes| - 1) { foreach ((node, neigh) in edges) { if (d[node] + w[node][neigh] < d[neigh]) { // try to relax edge (node, neigh) d[neigh] = d[node] + w[node][neigh]; // update the new distance from source to neigh p[neigh] = node; // save parent } } } // STEP 3: check if edge relaxations can still be made foreach ((node, neigh) in edges) { if (d[node] + w[node][neigh] < d[neigh]) { // try to relax edge (node, neigh) // negative cycle detected! return true, null, null; } } // STEP 4: no cycle detected return false, d, p; } // Usage example: has_cycle, d, p = Bellman-Ford(source, G=(nodes, edges)); if (has_cycle) { print "Has Cycle!" STOP. } else { // 1. Use distances from d // (e.g. d[node] = distance from source to node) // // 2. Rebuild path from node to source using parents (p) RebuildPath(source, destination, p); } ``` ### Exemple #### Exemplu Bellman-Ford {{https://ocw.cs.pub.ro/courses/_media/pa/new_pa/lab09-graph-bellman-example01.png?512| Exemplu Bellman-Ford}} Drumurile minime calculate de algoritmul lui Bellman-Ford sunt: |node|1|2|3|4|5| #newrow |d[node]|0|-2|-2|-3|-2| #newrow |p[node]|null|4|1|3|4| #newrow <spoiler Explicație pas cu pas> În exemplul atașat, avem un graf **orientat** cu următoare configurație: * `n = 5`, `m = 6` * Funcția de cost `w` are valorile menționate pe muchii. * Avem mai multe drumuri de cost diferite între diverse perechi de noduri din graf. * Alegem$ source = 1 $și rulăm pas cu pas algoritmul. * STEP 0: *$ d[node] = +∞$, pentru $node = 1:5n$ * $p[node] = null$, pentru $node = 1:5 $* STEP 1: initializări pentru sursă *$ d[1] = 0$ * $p[1] = null$ * STEP 2: Avem 5 noduri, relaxăm de 4 ori ($n - 1$ ori) toate muchiile din graf. Ordinea nu contează, pentru simplitate vom relaxa muchiile în ordine lexico-grafică: $(1, 2); (1, 3); (2, 3); (3, 4); (4, 2); (4, 5) $. * **iterație relaxare #1**: *$ (1, 2)$: Verificăm dacă $d[1] + w[1][2] < d[2]$ (adică $0 - 1 < +∞ $). **DA**, atunci **relaxarea muchiei are loc**: *$ d[2] = d[1] + w[1][2] = 0 - 1 = -1 $(actualizăm distanța) *$ p[2] = 1 $(actualizăm părintele de pe drum) *$ (1, 3)$: Verificăm dacă $d[1] + w[1][3] < d[3]$ (adică $0 - 2 < +∞ $). **DA**, atunci relaxarea muchiei are loc: *$ d[3] = 0 - 2 = -2$ * $p[3] = 1$ * $(2, 3)$: Verificăm dacă $d[2] + w[2][3] < d[3]$ (adică $-1 + 0 < -2). NU, atunci relaxarea muchiei NU are loc.

$(3, 4)$: Verificăm dacă $d[3] + w[3][4] < d[4]$ (adică $-2 - 1 < +∞$). DA, atunci relaxarea muchiei are loc:
- $d[4] = -2 - 1 = -3$
- $p[4] = 3$
$(4, 2)$: Verificăm dacă $d[4] + w[4][2] < d[2]$ (adică $-3 + 1 < -1). **DA**, atunci relaxarea muchiei are loc: *$ d[2] = -3 + 1 = -2$ * $p[2] = 3$ * $(4, 5)$: Verificăm dacă $d[4] + w[4][5] < d[2]$ (adică $-3 + 1 < +∞ $). **DA**, atunci relaxarea muchiei are loc: *$ d[5] = -3 + 1 = -2$ * $p[5] = 4 $* **iterație relaxare #2**: Nu se va relaxa nicio o muchie. * **iterație relaxare #3**: Nu se va relaxa nicio o muchie. * STEP 3: Se incearcă o etapă în plus (#4) de relaxări. Pentru că nu se mai poate relaxa muchii, înseamnă că distanțele găsite la `STEP 2` sunt finale și graful nu conține ciclu de cost negativ! * STOP. </spoiler> #### [Studiu de caz] Exemplu Bellman-Ford: detecție ciclu de cost negativ Dacă graful are un ciclu de cost negativ, se va putea plimba pe acel ciclu la infinit, reactulizând distanțele nodurilor implicate. <spoiler Exemplu detecție ciclu de cost negativ cu Bellman-Ford> {{https://ocw.cs.pub.ro/courses/_media/pa/new_pa/lab09-graph-bellman-example02.png?512| Exemplu Bellman-Ford - ciclu negativ}} În exemplul atașat, avem un graf **orientat** cu următoare configurație: * `n = 5`, `m = 6` * Funcția de cost `w` are valorile menționate pe muchii. * Avem mai multe drumuri de cost diferite între diverse perechi de noduri din graf. * Alegem$ source = 1 $și rulăm pas cu pas algoritmul. * STEP 0: *$ d[node] = +∞$, pentru $node = 1:5n$ * $p[node] = null$, pentru $node = 1:5 $* STEP 1: initializări pentru sursă *$ d[1] = 0$ * $p[1] = null$ * STEP 2: Avem 5 noduri, relaxăm de 4 ori ($n - 1$ ori) toate muchiile din graf. Ordinea nu contează, pentru simplitate vom relaxa muchiile în ordine lexico-grafică: $(1, 2); (1, 3); (2, 3); (3, 4); (4, 2); (4, 5) $. * **iterație relaxare #1**: *$ (1, 2)$: Verificăm dacă $d[1] + w[1][2] < d[2]$ (adică $0 - 1 < +∞ $). **DA**, atunci **relaxarea muchiei are loc**: *$ d[2] = d[1] + w[1][2] = 0 - 1 = -1 $(actualizăm distanța) *$ p[2] = 1 $(actualizăm părintele de pe drum) *$ (1, 3)$: Verificăm dacă $d[1] + w[1][3] < d[3]$ (adică $0 - 2 < +∞ $). **DA**, atunci relaxarea muchiei are loc: *$ d[3] = 0 - 2 = -2$ * $p[3] = 1$ * $(2, 3)$: Verificăm dacă $d[2] + w[2][3] < d[3]$ (adică $-1 - 2 < -2 $). **DA**, atunci relaxarea muchiei are loc: *$ d[3] = -1 -2 = -3$ * $p[3] = 2$ * $(3, 4)$: Verificăm dacă $d[3] + w[3][4] < d[4]$ (adică $-3 - 1 < +∞ $). **DA**, atunci relaxarea muchiei are loc: *$ d[4] = -3 - 1 = -4$ * $p[4] = 3$ * $(4, 2)$: Verificăm dacă $d[4] + w[4][2] < d[2]$ (adică $-4 + 1 < -1 $). **DA**, atunci relaxarea muchiei are loc: *$ d[2] = -3 + 1 = -2$ * $p[2] = 4$ * $(4, 5)$: Verificăm dacă $d[4] + w[4][5] < d[2]$ (adică $-3 + 1 < +∞ $). **DA**, atunci relaxarea muchiei are loc: *$ d[5] = -3 + 1 = -2$ * $p[5] = 4 $* **iterație relaxare #2**: *$ (1, 2)$: Verificăm dacă $d[1] + w[1][2] < d[2]$ (adică $0 - 1 < -2 $). **NU**, atunci relaxarea muchiei **NU** are loc. *$ (1, 3)$: Verificăm dacă $d[1] + w[1][3] < d[3]$ (adică $0 - 2 < -3 $). **NU**, atunci relaxarea muchiei **NU** are loc. *$ (2, 3)$: Verificăm dacă $d[2] + w[2][3] < d[3]$ (adică $-2 - 2 < -2 $). **DA**, atunci relaxarea muchiei are loc: *$ d[3] = -2 -2 = -4$ * $p[3] = 2$ * $(3, 4)$: Verificăm dacă $d[3] + w[3][4] < d[4]$ (adică $-4 - 1 < -4 $). **DA**, atunci relaxarea muchiei are loc: *$ d[4] = -4 - 1 = -5$ * $p[4] = 3$ * $(4, 2)$: Verificăm dacă $d[4] + w[4][2] < d[2]$ (adică $-5 + 1 < -2 $). **DA**, atunci relaxarea muchiei are loc: *$ d[2] = -5 + 1 = -4$ * $p[2] = 4$ * $(4, 5)$: Verificăm dacă $d[4] + w[4][5] < d[2]$ (adică $-5 + 1 < -2 $). **DA**, atunci relaxarea muchiei are loc: *$ d[5] = -5 + 1 = -4$ * $p[5] = 4 $* **iterație relaxare #3**: *$ (1, 2)$: Verificăm dacă $d[1] + w[1][2] < d[2]$ (adică $0 - 1 < -4 $). **NU**, atunci relaxarea muchiei **NU** are loc. *$ (1, 3)$: Verificăm dacă $d[1] + w[1][3] < d[3]$ (adică $0 - 2 < -4 $). **NU**, atunci relaxarea muchiei **NU** are loc. *$ (2, 3)$: Verificăm dacă $d[2] + w[2][3] < d[3]$ (adică $-4 - 2 < -4 $). **DA**, atunci relaxarea muchiei are loc: *$ d[3] = -4 -2 = -6$ * $p[3] = 2$ * $(3, 4)$: Verificăm dacă $d[3] + w[3][4] < d[4]$ (adică $-6 - 1 < -5 $). **DA**, atunci relaxarea muchiei are loc: *$ d[4] = -6 - 1 = -7$ * $p[4] = 3$ * $(4, 2)$: Verificăm dacă $d[4] + w[4][2] < d[2]$ (adică $-7 + 1 < -4 $). **DA**, atunci relaxarea muchiei are loc: *$ d[2] = -7 + 1 = -6$ * $p[2] = 4$ * $(4, 5)$: Verificăm dacă $d[4] + w[4][5] < d[2]$ (adică $-7 + 1 < -4 $). **DA**, atunci relaxarea muchiei are loc: *$ d[5] = -7 + 1 = -6$ * $p[5] = 4 $* STEP 3: Se incearcă o etapă în plus (#4) de relaxări. * **iterație relaxare #4**: *$ (1, 2)$: Verificăm dacă $d[1] + w[1][2] < d[2]$ (adică $0 - 1 < -6 $). **NU**, atunci relaxarea muchiei **NU** are loc. *$ (1, 3)$: Verificăm dacă $d[1] + w[1][3] < d[3]$ (adică $0 - 2 < -6 $). **NU**, atunci relaxarea muchiei **NU** are loc. *$ (2, 3)$: Verificăm dacă $d[2] + w[2][3] < d[3]$ (adică $-6 - 2 < -6 $). **DA**, atunci relaxarea muchiei **se poate face**. * În acest moment putem trage **concluzia că avem un ciclu de cost negativ în graf**, căci altfel distanțele ar fi fost finale și nu am mai fi putut relaxa ceva în `STEP 3`. * STOP. </spoiler> ### Complexitate * **complexitate temporală**:$ T = O(n * m)\ sau\ O(|V| * |E|) $* **complexitate spațială** :$ S = O(1) $<spoiler Detalii (analiză + optimizări)> * **complexitate temporală**: Algoritmul relaxează de **n** ori toate cele **m** muchii din graf. * **complexitate spațială** : Nu avem memorie spațială auxialiară. ATENȚIE! Vom aloca tablourile$ d$ / $p $, însă acestea nu sunt specifice algoritmului. * **optimizare**: Se poate obține o performanță mai bună în practică, dar cu aceeași complexitate asimptotică, folosind o coadă: * Dacă$ d[node]$ nu a fost schimbată la un pas, folosirea muchiilor care pornesc din $node $nu produce efecte. * Se poate ţine o coadă de noduri, la fiecare pas scoţând un element din aceasta. Se va încerca relaxarea muchiilor care pornesc din nodul scos. Nodurile cu distanțe actualizate se reintroduc în coadă. * Dacă un nod a fost scos de **n** ori din coadă, atunci graful conține cel puțin un ciclu de cost negativ. </spoiler> ## TLDR * Pentru **topologii particulare** ale problemei **shortest-paths**, vom folosi mereu un algoritm baza pe o parcugere (de exemplu, sortare topologic la DAG). Folosirea algoritmilor Dijkstra / Bellman-Ford ar duce la o soluție ineficientă pentru aceste cazuri particulare! * Pe **topologii generale**, pentru **single-source shortest-paths problem**, vom folosi Dijkstra / Bellman-Ford. * **Dijkstra** are complexitate mai bună, deci este de preferat, însă acesta se poate folosi doar pe grafuri cu costuri **nenegative**. * Dacă avem muchii cu costuri negative, suntem obligați să folosim **Bellman-Ford**, care ne poate detecta și prezența ciclurilor de cost negativ. 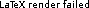* Dacă avem mai multe surse / destinații, putem rula pentru fiecare sursă Dijkstra /Bellman-Ford, obținând complexitate$ O(n * m * log n)$ / $O(n^2 * m) $. Vom vedea în laboratorul următor cum putem îmbunătăți acest lucru. ## Exerciții <note> Scheletul de laborator se găsește pe pagina [[https://github.com/acs-pa/pa-lab/tree/main/skel/lab09|pa-lab::skel/lab09]]. </note> <note warning> Înainte de a rezolva exercițiile, asigurați-vă că ați citit și înțeles toate precizările din secțiunea [[https://ocw.cs.pub.ro/courses/pa/skel_graph | Precizari laboratoare 07-12]]. Prin citirea acestor precizări vă asigurați că: * știți **convențiile** folosite * evitați **buguri** * evitați **depunctări** la lab/teme/test </note> ### Dijkstra Se dă un graf **orientat** cu **n** noduri și **m** arce. Graful are pe arce **costuri pozitive** (nenegative). Folosiți **Dijkstra** pentru a găsi **costul minim** (**lungimea minimă**) a unui drum de la o sursă dată (**source**) la toate celelalte$ n - 1 $noduri din graf. <note warning> Restricții și precizări: *$ n ⇐ 50.000 $ * $ m ⇐ 2.5 * 10^5 $ * $ 0 ⇐ c ⇐ 20.000 $, unde c este costul/lungimea unui arc * timp de execuție * C++: `1s` * Java: `2s` </note> <note> Rezultatul se va returna sub forma unui vector **d** cu **n + 1** elemente. Convenție: *$ d[node] $= costul minim / lungimea minimă a unui drum de la **source** la nodul **node** *$ d[source] = 0 $*$ d[node] = -1 $, dacă nu se poate ajunge de la **source** la **node**$ d[0] $nu este folosit, deci ca fi initializat cu 0! (am pastrat indexarea nodurilor de la 1). </note> ### RebuildPath S-a rulat anterior un algoritm oarecare de calculare a drumurilor de lungime minimă într-un graf cu **n** noduri și **m** arce folosind sursa **source**. Se cunoaște vectorul de părinți$ p $rezultat: *$ p[node] $= părintele lui node de pe drumul minim de la sursă la node. *$ p[source] = 0 $- sursa nu are părinte. *$ p[node] = 0$ - nodul $node$ nu este accesibil din $source $. Se cere să se reconstituie drumul de la nodul **source** la nodul **destination**. <note warning> Restricții și precizări: *$ n ⇐ 50.000 $* timp de execuție * C++: `1s` * Java: `2s` </note> <note> Rezultatul se va returna sub forma unui vector **path**:$ path = (source, …, destination) $. </note> ### Bellman-Ford Se dă un graf **orientat** cu **n** noduri și **m** arce. Graful are pe arce **costuri oarecare** (pozitive sau negative). Folosiți **Bellman-Ford** pentru a găsi **costul minim** (**lungimea minimă**) a unui drum de la o sursă dată (**source**) la toate celelalte$ n - 1$ noduri din graf. Se va folosi aceeași convenție de reprezentare a vectorului de distanțe $d $. <note warning> Restricții și precizări: *$ n ⇐ 50.000 $ * $ m ⇐ 2.5 * 10^5 $ * $ -1000 ⇐ c ⇐ +1000$, unde c este costul/lungimea unui arc

* timp de execuție

C++: `1s`
Java: `2s`

</note>

### BONUS La acest laborator, asistentul va alege 1-2 probleme din secțiunea extra.

### Extra * [infoarena/distante](https://infoarena.ro/problema/distante) * [infoarena/catun](https://infoarena.ro/problema/catun) * [infoarena/lanterna](https://infoarena.ro/problema/lanterna) * [infoarena/ciclu](https://infoarena.ro/problema/ciclu) * [codeforces/the-classic-probem](https://codeforces.com/contest/464/problem/E) * [codeforces/planets](https://codeforces.com/contest/229/problem/B) * [acm/sightseeingtrip](http://poj.org/problem?id=1734)

## Referințe

[0] Chapters Single-Source Shortest Paths / All-Pairs Shortest Paths, “Introduction to Algorithms”, Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest and Clifford Stein.