• Însuşirea conceptului de arbore minim de acoperire;
• Înţelegerea modului de funcţionare a algoritmilor de determinare a unui arbore minim de acoperire prezentaţi;
• Aplicarea algoritmilor în rezolvarea problemelor;

Găsirea unui arbore minim de acoperire pentru un graf are aplicaţii în domenii cât se poate de variate:

• Reţele (de calculatoare, telefonie, cablu TV, electricitate, drumuri): se doreşte interconectarea mai multor puncte, cu un cost redus şi atunci este utilă cunoaşterea arborelui care conectează toate punctele, cu cel mai mic cost posibil. STP(Spanning Tree Protocol) este un protocol de rutare care previne apariţia buclelor într-un LAN, şi se bazează pe crearea unui arbore de acoperire. Singurele legături active sunt cele care apar în acest arbore, iar astfel se evită buclele.
• Segmentarea imaginilor: împărţirea unei imagini în regiuni de pixeli cu proprietăţi asemănătoare. E utilă mai apoi în analiza medicală a unei zone afectate de o tumoare de exemplu.
• Algoritmi de aproximare pt probleme NP-dure: problema comis-voiajorului, arbori Steiner.
• Clustering: pentru detectarea de clustere cu forme neregulate [8], [9].

Dându-se un graf conex neorientat G =(V, E), se numeşte arbore de acoperire al lui G un subgraf G’=(V, E’) care conţine toate vârfurile grafului G şi o submulţime minimă de muchii E’⊆ E cu proprietatea că uneşte toate vârfurile şi nu conţine cicluri. Cum G’ este conex şi aciclic, el este arbore. Pentru un graf oarecare, există mai mulţi arbori de acoperire.

Dacă asociem o matrice de costuri, w, pentru muchiile din G, fiecare arbore de acoperire va avea asociat un cost egal cu suma costurilor muchiilor conţinute. Un arbore care are costul asociat mai mic sau egal cu costul oricărui alt arbore de acoperire se numeşte arbore minim de acoperire (minimum spanning tree) al grafului G. Un graf poate avea mai mulţi arbori minimi de acoperire. Dacă toate costurile muchiilor sunt diferite, există un singur AMA. Primul algoritm pentru determinarea unui arbore minim de acoperire a fost scris în 1926 de Otakar Boruvka. În prezent, cei mai folosiţi algoritmi sunt Prim şi Kruskal. Toţi trei sunt algoritmi greedy, şi rulează în timp polinomial. La fiecare pas, pentru a construi arborele se alege cea mai bună variantă posibilă la momentul respectiv. Generic, algoritmul de determinare a unui AMA se poate scrie astfel:

ArboreMinimDeAcoperire(G(V, E), c)
	MuchiiAMA = ∅;
	while (MuchiiAMA nu reprezintă muchiile unui arbore minim de acoperire)
		găseşte o muchie (u, v) care este sigură pentru MuchiiAMA;
		MuchiiAMA = MuchiiAMA ∪ {(u, v)};
	return MuchiiAMA;

O muchie sigură este o muchie care se poate adăuga unei submulţimi de muchii ale unui arbore minim de acoperire, astfel încât noua mulţime obţinută să aparţină tot unui arbore minim de acoperire. Iniţial, MuchiiAMA este o mulţime vidă. La fiecare pas, se adaugă câte o muchie sigură, deci MuchiiAMA rămâne o submulţime a unui AMA. În consecinţă, la sfarşitul rulării algoritmului (când muchiile din mulţime unesc toate nodurile din graf), MuchiiAMA va conţine de fapt arborele minim de acoperire dorit.

Algoritmul a fost dezvoltat în 1956 de Joseph Kruskal. Determinarea arborelui minim de acoperire se face prin reuniuni de subarbori minimi de acoperire. Iniţial, se consideră că fiecare nod din graf este un arbore. Apoi, la fiecare pas se selectează muchia de cost minim care uneşte doi subarbori disjuncţi, şi se realizează unirea celor doi subarbori. Muchia respectivă se adaugă la mulţimea MuchiiAMA, care la sfârşit va conţine chiar muchiile din arborele minim de acoperire.

Kruskal(G(V, E), w)
MuchiiAMA <- ∅;
for each v in V do
	MakeSet(v);	//fiecare nod e un arbore diferit
sort(E);		//sortează muchiile în ordine crescătoare a costului
for each (u,v) in E do
if (FindSet(u) != FindSet(v)) then	//capetele muchiei fac parte //din subarbori disjuncţi
		MuchiiAMA = MuchiiAMA ∪ {(u, v)};	//adaugă muchia la arbore
Union(u, v);    //uneşte subarborii corespunzători lui u şi v
return MuchiiAMA;

Bucla principală for poate fi înlocuită cu o buclă while, în care se verifică dacă în MuchiiAMA există mai puţin de |V| - 1 muchii, pentru că orice arbore de acoperire are |V| - 1 muchii, iar la fiecare pas se adaugă o muchie sigură.

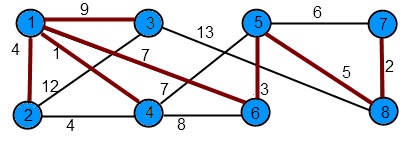
Se consideră graful din figura următoare:

Fiecare subarbore va fi colorat diferit. Cum iniţial fiecare nod reprezintă un subarbore, nodurile au culori diferite. Pe măsură ce subarborii sunt uniţi, nodurile aparţinând aceluiaşi subarbore vor fi coloraţi identic. Costurile muchiilor sunt sortate în ordine crescătoare.

Pas 1

Se alege prima muchie, (1,4). Se observă că uneşte subarborii {1} şi {4}, deci muchia e adăugată la MuchiiAMA, iar cei doi subarbori se unesc. 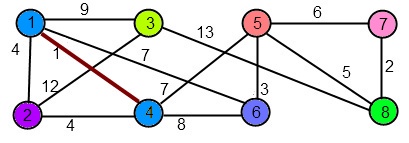MuchiiAMA = {(1,4)}.

Pas 2

Următoarea muchie este (7,8), care uneşte {7} şi {8}. Se adaugă la MuchiiAMA şi se unesc cei doi subarbori. MuchiiAMA = {(1,4),(7,8)}.

Pas 3

Următoarea muchie este (5,6), care uneşte {5} şi {6}. Se adaugă la MuchiiAMA şi se unesc cei doi subarbori. 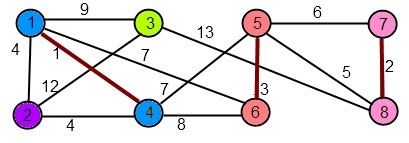MuchiiAMA = {(1,4),(7,8),(5,6)}.

Pas 4

Următorul cost este 4. Se observă că muchiile (1,2) şi (2,4) au costul 4 şi unesc {2} cu {1,4}. Se adaugă la MuchiiAMA una dintre cele două muchii, fie ea (1,2), şi se unesc cei doi subarbori. Alegerea muchiei (2,4) va duce la găsirea unui alt AMA. [Am spus anterior că un graf poate avea mai mulţi arbori minimi de acoperire, cu acelaşi cost, dacă există muchii diferite cu acelaşi cost.] 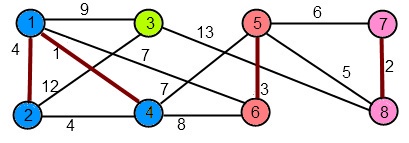MuchiiAMA = {(1,4),(7,8),(5,6),(1,2)}.

Pas 5

Următoarea muchie de cost minim este (5,8), care uneşte {5,6} şi {7,8}. Se adaugă la MuchiiAMA şi se unesc cei doi subarbori, rezultând {5,6,7,8}. MuchiiAMA = {(1,4),(7,8),(5,6),(1,2), (5,8)}.

Pas 6

Muchia (5,7), care are cel mai mic cost actual, are ambele extremităţi în subarborele {5,6,7,8}. În consecinţă, nu se efectuează nicio schimbare.

MuchiiAMA = {(1,4),(7,8),(5,6),(1,2),(5,8)}.

Pas 7

Următorul cost este 7. Se observă că muchiile (1,6) şi (4,5) au costul 7 şi unesc subarborii {1,2,4} şi {5,6,7,8}. Se adaugă la MuchiiAMA (1,6), şi se unesc cei doi subarbori. Alegerea muchiei (4,5) va duce la găsirea unui alt AMA. 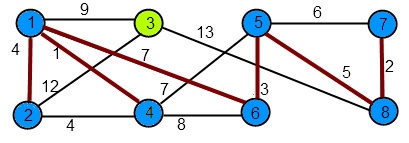MuchiiAMA = {(1,4),(7,8),(5,6),(1,2),(5,8),(1,6)}.

Pas 8

Muchia (4,6) de cost 8 are capetele în acelaşi subarbore, deci nu se produc schimări.

MuchiiAMA = {(1,4),(7,8),(5,6),(1,2),(5,8),(1,6)}.

Pas 9

Muchia (1,3) de cost 9 uneşte cei doi subarbori rămaşi, {1,2,4,5,6,7,8} şi {3}. Deci după unire obţinem un singur arbore. (1,3) se adaugă la MuchiiAMA, care va conţine acum 7 muchii, iar algoritmul se opreşte. Arborele minim de acoperire obţinut este {(1,4),(7,8),(5,6),(1,2),(5,8),(1,6), (1,3)}.Costul său se calculează însumând costurile tuturor muchiilor:

Cost(MuchiiAMA) = 1 + 2 + 3 + 4 + 5 + 7 + 9 = 31

Alţi arbori minimi de acoperire pentru exemplul propus sunt: * {(1,4),(7,8),(5,6),(1,2),(5,8),(4,5), (1,3)} * {(1,4),(7,8),(5,6),(2,4),(5,8),(1,6), (1,3)} * {(1,4),(7,8),(5,6),(2,4),(5,8),(4,5), (1,3)}.

Pentru alte exemple explicate consultaţi [2], [3] şi [5].

Iniţializările se fac în O(|V|). Bucla principală while se execută de |V| ori. Procedura GetMin() are nevoie de un timp de ordinul O(lg|V|), deci toate apelurile vor dura O(|V|lg|V|). Bucla for este executată în total de O(|E|) ori, deoarece suma tuturor listelor de adiacenţă este 2|E|. Modificarea distanţei, a predecesorului, şi refacerea heapului se execută într-un timp de O(1), O(1) şi respectiv O(lg|V|). Deci în total bucla interioară for durează O(|E|lg|V|).

În consecinţă, timpul total de rulare este O(|V|lg|V|+|E|lg|V|), adică O(|E|lg|V|). Aceeaşi complexitate s-a obţinut şi pentru algoritmul Kruskal. Totuşi, timpul de execuţie al algoritmului Prin se poate îmbunătăţi până la O(|E|+|V|lg|V|), folosind heap-uri Fibonacci.

Un arbore minim de acoperire al unui graf este un arbore care conţine toate nodurile, şi în plus acestea sunt conectate prin muchii care asigură un cost total minim. Determinarea unui arbore minim de acoperire pentru un graf este o problemă cu aplicaţii în foarte multe domenii: reţele, clustering, prelucrare de imagini. Cei mai cunoscuţi algoritmi, Prim şi Kruskal, rezolvă problema în timp polinomial. Performanţa algoritmilor depinde de modul de reprezentare a structurilor de date folosite.

[1] – http://en.wikipedia.org/wiki/Minimum_spanning_tree

[2] – T. Cormen, C. Leiserson, R. Rivest, C. Stein – Introducere în Algoritmi, cap. 24

[3] – http://en.wikipedia.org/wiki/Kruskal%27s_algorithm

[4] – http://en.wikipedia.org/wiki/Prim%27s_algorithm

[5] – http://w3.cs.upt.ro/~calin/resources/sdaa/kruskal.ppt

[6] – http://www.cs.upt.ro/~calin/resources/sdaa/prim.ppt

[7] – http://www.cs.princeton.edu/~wayne/kleinberg-tardos/04mst.pdf

[8] – http://hc.ims.u-tokyo.ac.jp/JSBi/journal/GIW01/GIW01F03.pdf

[9] – http://www4.ncsu.edu/~zjorgen/ictai06.pdf

[10] – C. Giumale – Introducere în Analiza Algoritmilor, cap.5.5

Datorita miscarilor politice la nivel inalt, Gigel, dictatorul Bitlandiei, doreste sa isi construiasca un palat buncar antinuclear. Buncarul este format din N camere conectate prin coridoare. Coridoarele dintre camere sunt destul de scumpe de construit asa ca Gigel doreste sa construiasca cat mai putine si cat mai ieftine astfel incat tot sa aiba acces in toate camerele. El va da 2 planuri si voi trebuie sa folositi 2 algoritmi diferiti (Prim [4p] si Kruskal [4p]) pentru a determina care este cea mai buna alegere de coridoare.

Pornind de la un algoritm AMA se cere să se contruiască aleator un labirint care suportă un drum de ieșire din orice locație interioară. Ulterior, trebuie să găsiți drumul spre ieșire dintr-o poziție dată folosind o parcurgere DFS.