This is an old revision of the document!
Laborator 4: Programare Dinamică (continuare)
Responsabili:
Autori:
Obiective laborator
- Înțelegerea noțiunilor de bază despre programarea dinamică.
- Însușirea abilităților de implementare a algoritmilor bazați pe programarea dinamică.
Precizări inițiale
Exemplele de cod apar încorporate și în textul laboratorului pentru a facilita parcurgerea cursivă a acestuia. ATENȚIE! Varianta actualizată a acestor exemple se găsește întotdeauna pe GitHub.
- Toate bucățile de cod prezentate în partea introductivă a laboratorului (înainte de exerciții) au fost testate. Cu toate acestea, este posibil ca, din cauza mai multor factori (formatare, caractere invizibile puse de browser, etc.), un simplu copy-paste să nu fie de ajuns pentru a compila codul.
- Vă rugăm să compilați DOAR codul de pe GitHub. Pentru raportarea problemelor, contactați unul dintre maintaineri.
- Pentru orice problemă legată de conținutul acestei pagini, vă rugam să dați e-mail unuia dintre responsabili.
Ce este DP?
Similar cu greedy, tehnica de programare dinamică este folosită pentru rezolvarea problemelor de optimizare. În continuare vom folosi acronimul DP (dynamic programming).
De asemenea, DP se poate folosi și pentru probleme în care nu căutam un optim, cum ar fi problemele de numărare.
Pentru noțiunile prezentate până acum despre DP, vă rugăm să consultați pagina laboratorului 3.
Exemple clasice
Programarea Dinamică este cea mai flexibilă tehnică a programării. Cel mai ușor mod de a o înțelege presupune parcurgerea cât mai multor exemple.
Propunem câteva categorii de recurențe pe care le vom grupa astfel:
- recurențe de tip SSM (Subsecvență de Sumă Maximă)
- recurențe de tip RUCSAC
- recurențe de tip PODM (Parantezare Optimă de Matrice)
- recurențe de tip numărat
- recurențe pe grafuri
Categoria 3: PODM
Aceste recurențe au o oarecare asemănare cu problema PODM (enunț + soluție).
ATENȚIE! Acest tip de recurențe poate fi mai greu (decât celelalte). Puteți consulta acasă materialele puse la dispoziție pentru a înțelege mai bine această categorie.
Caracteristici:
- Acest tip de problemă presupune că o putem formula ca pe o problemă de tip subinterval $[i, j]$.
- Dacă dorim să găsim optimul pentru acest interval, va trebui să luăm în calcul toate combinațiile de 2 subprobleme care ar putea genera o soluție pentru problemele $[i, j]$.
- Se consideră fiecare divizare în 2 subprobleme, dată de intermediarul k, astfel:
- Fie $[i, k]$ și $[k + 1, j]$ cele 2 subprobleme pentru care cunoaștem soluțiile, atunci o soluție pentru $[i,j]$ se poate obține îmbinându-le pe cele două
- pentru a gasi soluția cea mai bună:
- vom itera prin toate valorile k posibile
- o vom alege pe cea care maximizează soluția problemei $[i,j]$
- Calculul se face de la intervale mici (probleme ușoare - $[i,i]$ sau $[i, i+1]$) spre probleme generale (dimensiune generală - $[i, j]$ ). În final, se ajunge și la dimensiunile inițiale ($[1, n]$).
- Privind imaginea de ansamblu, adică modul în care se completează matricea dp, observăm că aceasta se completează diagonală cu diagonală.
Exemple clasice
PODM
Enunț
Fie un produs matriceal $M = M_1 M_2 ... M_n$. Putem pune paranteze în mai multe moduri și vom obține același rezultat (înmulțire asociativă), dar este posibil să obținem un număr diferit de înmulțiri scalare.
Matricea $M_i$ are (prin convenție), dimensiunile $d_{i-1} d_{i}$.
Cerință
Se cere să se găsească o parantezare optimă de matrice (PODM), adică să se găsească o parantezare care să minimizeze numărul de înmulțiri scalare.
Exemple
TIPAR
A fost descris în detaliu mai sus (când s-a vorbit de categorie).
Numire recurență
$dp[i][j]$ = numărul minim de înmulțiri scalare cu care se poate obține produsul $M_i * M_{i+1} * ... *{M_j}$
Găsire recurență
- Cazul de bază :
- $dp[i][i] = 0 $
- NU avem niciun efort dacă nu avem ce înmulți.
- $dp[i][i+1] = d_{i-1} d_{i} d_{i+1}$
- Dacă avem două matrice, putem doar să le înmulțim. Nu are sens să folosim paranteze.
- Daca înmulțim 2 matrice de dimensiuni $d_{i-1} * d_{i}$ și $d_{i} * d_{i + 1}$, avem costul $d_{i-1} d_{i} d_{i+1}$
- Cazul general: $dp[i][j] = min(dp[i][k] + dp[k+1][j] + d_{i-1} d_{k} d_{j})$, unde $k = i : j - 1$
- dacă avem de efectuat șirul de înmulțiri $M_i ... M_j$, atunci putem pune paranteze oriunde și să facem înmulțirile astfel $(M_i ... M_k) (M_{k+1} ... M_{j})$
- costul minim pentru $(M_i ... M_k)$ este $dp[i][k]$
- costul minim pentru $(M_{k+1} ... M_j)$ este $dp[k + 1][j]$
- vom avea, în final, de înmulțit 2 matrice de dimensiune $d_{i-1} * d_{k}$ si $d_{k} * d_{j}$, operație care are costul $d_{i-1}d_{k}d_{j}$
- însumăm cele 3 costuri intermediare
Implementare
Puteți rezolva și testa problema PODM pe infoarena aici.
Un exemplu de implementare în C++ se găsește mai jos.
Complexitate
Întrucat soluția presupune fixarea capetelor unui subinterval (i, j), apoi alegerea unui intermediar (k), complexitatea este dată de aceste 3 cicluri.
- complexitate temporală: $T(n) = O(n^3)$
- complexitate spațială: $S(n) = O(n^2)$
Categoria 4: NUMĂRAT
Aceste recurențe au o oarecare asemănare:
- toate numară lucruri! :p
- interesante sunt cazurile când numărul căutat este foarte mare (altfel am putea apela la alte metode - ex. generarea tuturor candidaților posibili cu backtracking)
- în acest caz, deoarece numărul poate să nu încapă pe un tip reprezentabil standard (ex. int pe 32/64 de biți), se cere (de obicei) restul împarțirii numărului căutat la un număr MOD (vom folosi în continuare această notație).
Sfaturi / Reguli
- când căutați o recurență pentru o problema de numărare trebuie să aveți grijă la două aspecte:
- 1) să NU numărați același obiect de două ori.
- 2) să numărați toate obiectele în cauză.
- de multe ori, o problemă de numărare implică o partiționare a tuturor posibilelor soluții după un anumit criteriu (relevant). Găsirea criteriului este partea esențială pentru aflarea recurenței.
Regulile de lucru cu clase de resturi
Reamintim câteva proprietăți matematice pe care ar trebui să le aveți în vedere atunci când implementați pentru a obține corect resturile anumitor expresii. (corect poate să însemne, de exemplu, să evitați overflow :D - lucru neintuitiv câteodată).
- proprietăți de bază:
- $(a + b) \ \% \ MOD = ((a \ \% \ MOD) + (b \ \% \ MOD)) \ \% \ MOD $
- $(a \ * b) \ \% \ MOD = ((a \ \% \ MOD) \ * (b \ \% \ MOD)) \ \% \ MOD $
- $(a - b) \ \% \ MOD = ((a \ \% \ MOD) - (b \ \% \ MOD) + MOD) \ \% \ MOD $ (restul nu poate fi ceva negativ; în C++ % nu funcționează pe numere negative)
- invers modular
- $ \frac{a}{b} \ \% \ MOD = ((a \ \% \ MOD) * (b ^ {MOD-2} \ \% \ MOD)) \ \% \ MOD)$
- DACĂ MOD este prim; DACĂ a și b nu sunt multipli ai lui MOD
- C++
- 1LL / 1ULL - constanta 1 pe 64 biti cu semn / făra semn
- 1LL * a * b - am grijă ca rezultatul să nu dea overflow și să se stocheze direct pe 64 biți (cu semn)
- Java
- 1L - constanta 1 pe 64 biți cu semn (în Java nu există unsigned types)
- 1L * a * b - am grijă ca rezultatul să nu dea overflow și să se stocheze direct pe 64 biți (cu semn)
Gardurile lui Gigel
Enunt
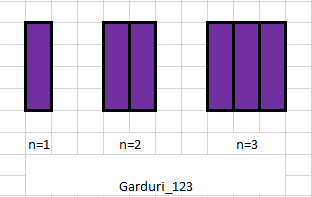
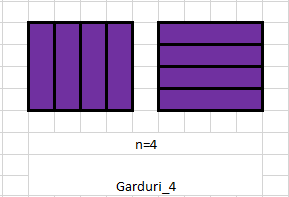
Gigel trece de la furat obiecte cu un rucsac la numarat garduri (fiecare are micile lui placeri :D). El doreste sa construiasca un gard folosind in mod repetat un singur tip de piesa.
O piesa are dimensiunile 4 x 1 (o unitate = 1m). Din motive irelevante pentru aceasta problema, orice gard construit trebuie sa aiba inaltime 4m in orice punct.
O piesa poate fi pusa in pozitie orizontala sau in pozitie verticala.
Cerinta
Gigel se intreaba cate garduri de lungime n si inaltime 4 exista? Deoarece celalalt prenume al lui este Bulănel, el intuieste ca acest numar este foarte mare, de aceea va cere restul impartirii acestui numar la 1009.
Recurenta
Numire recurenta
$dp[i] $ = numarul de garduri de lungime i si inaltime 4 (nimic special - exact ceeea ce se cere in enunt)
Raspunsul la problema este $dp[n]$.
Gasire recurenta
- Caz de baza
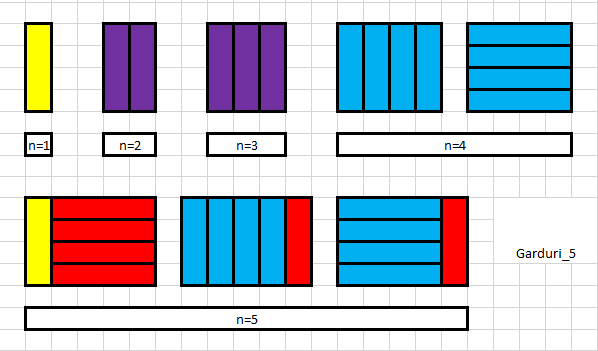
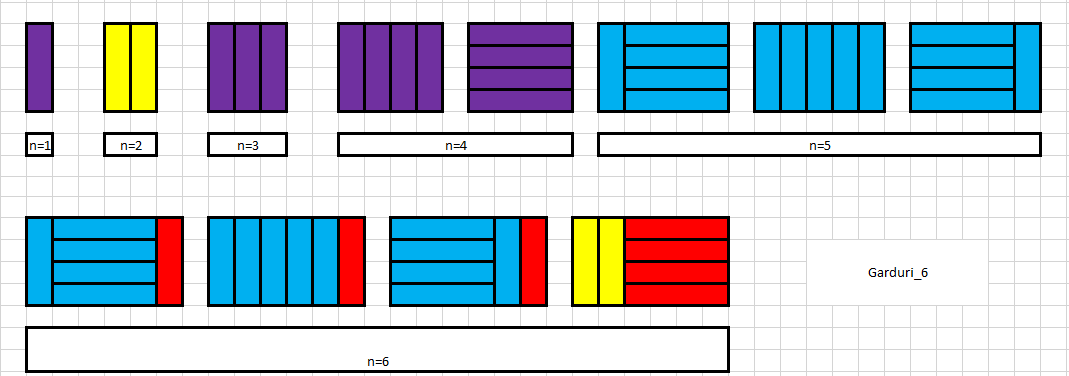
- $dp[1] = dp[2] = dp[3] = 1$; $dp[4]$ = 2
- Caz general
- atunci dorim sa formam un gard de lungime i ($ i >= 5 $) am vazut ca putem alege cum sa punem ultima/ultimele piese
- DACA alegem ca ultima piesa sa fie pusa in pozitie verticala, atunci la stanga mai ramane de completat un subgard de lungime $i-1$
- numarul de moduri in care putem face acest subgard este $dp[i-1]$
- DACA alegem ca ultima piesa sa fie in pozitie orizontala (de fapt punem 4 piese in pozitie orizontala), atunci la stanga mai ramane de completat un subgard de lungime $i-4$
- numarul de moduri in care putem face acest subgard este $dp[i-4]$
- $dp[i] = (dp[i-1] + dp[i-4]) \ \% \ MOD$
De asemenea tot in sectiunea sfaturi si reguli am precizat ca nu vrem sa numaram un obiect (un mod de a construi gardul) de doua ori. Recurenta noastra (dp[i] = dp[i-1] + dp[i-4]) nu ia un obiect de doua ori pentru ca orice solutie care vine din dp[i-4] e diferita de alta care vine din dp[i-1] pentru ca difera in cel putin ultima scandura asezata)
Implementare recurenta
Aici puteti vedea un exemplu simplu de implementare in C++.
Complexitate
- complexitate temporala: $T = O(n)$
- explicatie: avem o singura parcurgere in care construim tabloul dp
- se poate obtine $T=O(log n)$ folosind exponentiere pe matrice!
- complexitate spatiala: $S = O(n)$
- explicatie: stocam tabloul dp
- se poate ontine $S = O(1)$ folosind exponentiere pe matrice!
Tehnici folosite in DP
De multe ori este nevoie sa folosim cateva tehnici pentru a obtine performanta maxima cu recurenta gasita.
In laboratorul 3 se mentiona tehnica de memoizare (in prima parte a laboratorului). In acesta ne vom rezuma la cum putem folosi cunostintele de lucru matricial pentru a favoriza implementarea unor anumite tipuri de recurente.
Exponentiere pe matrice pentru recurente liniare
Recurente liniare
O recurenta liniara in contextul laboratorului de DP este de forma:
- $dp[i] = \sum_{k=1}^{KMAX} c_k * dp[i - k]$
- pentru KMAX o constanta
- de obicei, KMAX este foarte mica comparativ cu dimensinea n a problemei
- $c_k$ constante reale (unele pot fi nule)
O astfel de recurenta ar insemna ca pentru a calcula costul problemei i , imbinam costurile problemelor $i - 1, i-2, ...., i-k$, fiecare contribuind cu un anumit coeficient $c_{1}, c_{2}, ..., c_{k}$.
Exponentiere pe matrice
Facem urmatoarele notatii:
- $S_i$ = starea la pasul i
- $S_i = (dp[i - k + 1], dp[i - k + 2], ..., dp[i - 1], dp[i])$
- $S_k$ = starea initiala (in care cunoaste cele k cazuri de baza)
- $S_k = (dp[1], dp[2], ..., dp[k-1], dp[k])$
- $C$ = matrice ce coeficienti constanti
- are dimensiune $KMAX * KMAX$
- putem pune constante in clar
- putem pune constantele $c_k$ care tin de problema curenta
Algoritm naiv
Putem formula problema astfel:
- $S_k$ = este starea initiala
- pentru a obtine starea urmatoare, aplicam algoritmul urmator
- $S_i = S_{i-1}C$
Determinare C
Pentru a determina elementele matricei C, trebuie sa ne uitam la inmultirea matriceala de mai sus si sa alegem elementele lui C astfel incat prin inmultirealui $S_{i-1}$ cu $C$ sa obtinem elementele din $S_i$.
\begin{gather} \begin{bmatrix} dp[i - k + 1] & ... & dp[i-1] & dp[i] \\ \end{bmatrix} = \begin{bmatrix} dp[i - k] & ... & dp[i-2] & dp[i-1] \\ \end{bmatrix} \begin{bmatrix} 0 & 0 &... & 0 & 0 & c_{k}\\ 1 & 0 &... & 0 & 0 & c_{k-1}\\ 0 & 1 &... & 0 & 0 & c_{k-2}\\ ... & ... & ... & ... & ...\\ 0 & 0 &... & 1 & 0 & c_{2}\\ 0 & 0 &... & 0 & 1 & c_{1}\\ \end{bmatrix} \end{gather}
Exponentiere logaritmica pe matrice
Algoritmul naiv de mai sus are dezavantajul ca are tot o complexitate temporala $O(n)$.
Sa executam cativa pasi de inductie pentru a vedea cum este determinat $S_i$. $$S_i = S_{i-1}C$$ $$S_i = S_{i-2}C^2$$ $$S_i = S_{i-3}C^3$$ $$...$$ $$S_i = S_{k}C^{i -k}$$
In laboratorul 2 (Divide et Impera) am invatat ca putem calcula $ x ^ n $ in timp logaritmic. Deoarece si inmultirea matricilor este asociativa, putem calcula $C ^ n$ in timp logaritmic.
Obtinem astfel o solutie cu urmatoarele complexitati:
- complexitate temporala : $T = O(KMAX^3 * log(n))$
- explicatie
- facem doar $O(log n)$ pasi, dar un pas implica inmultire de matrice
- o inmultire de matrice patratica de dimensiune KMAX are $KMAX^3$ operatii
- aceasta metoda este eficienta cand $KMAX << n$ (KMAX este mult mai mic decat n)
- complexitatea spatiala : $S = O(KMAX^3)$
- explicatie
- este nevoie sa stocam cateva matrici
Observatie! In ultimele calcule nu am sters contanta KMAX, intrucat apare la puterea a 3-a! $KMAX = 100$ implica $KMAX^3 = 10^6$, valoare care nu mai poate fi ignorata in practica ($KMAX^3$ poate fi comparabil cu n).
Gardurile lui Gigel (optimizare)
Dupa cum am vazut mai sus, in problema cu garduri data de Gigel solutia este o recurenta liniara:
- $dp[1] = dp[2] = dp[3] = 1$; $d[4]=2$;
- $dp[i] = dp[i - 1] + dp[i - 4]$, pentru $i > 4$
Exponentiere rapida
- $ k = 4 $
- $S_4 = (dp[1], dp[2], dp[3], dp[4]) = (1, 1, 1, 4)$
- $S_i = (dp[i-3], dp[i-2], dp[i-1], dp[i])$
- Raspunsul se afla efectuand operatia $S_n = S_4 * C^{n - 4}$, unde C are urmatorul continut:
\begin{gather} C = \begin{bmatrix} 0 & 0 & 0 & 1\\ 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 1\\ \end{bmatrix} \end{gather}
Exercitii
DP or math?
Fie un sir de numere naturale strict pozitive. Cate subsiruri (submultimi nevide) au suma numerelor para?
Task-uri:
- Se cere o solutie folosind DP.
- Inspectand recurenta gasita la punctul precedent, incercati sa o inlocuiti cu o formula matematica.
- Care este complexitatea pentru fiecare solutie (timp + spatiu)? Care este mai buna? De ce? :D
Deoarece rezultatul poate fi prea mare, se cere restul impartirii lui la $1000000007$ ($10^9 + 7$).
Pentru punctaj maxim pentru aceasta problema, este necesar sa rezolvati toate subpunctele (ex. nu folositi direct formula, gasiti mai intai recurenta DP). Trebuie sa implementati cel putin solutia cu DP.
In problemele de numarat, exista o sansa buna sa putem gasi (si) o formula matematica, care poate fi implementata intr-un mod mai eficient decat o recurenta DP.
Expresie booleana
Se da o expresie booleana corecta cu n termeni. Fiecare din termeni poate fi unul din stringurile true, false, and, or, xor.
Numarati modurile in care se pot aseza paranteze astfel incat rezultatul sa fie true. Se respecta regulile de la logica (tabelele de adevar pentru operatiile and, or, xor).
Deoarece rezultatul poate fi prea mare, se cere restul impartirii lui la $1000000007$ ($10^9 + 7$).
- false: 'F'
- true: 'T'
- and: '&'
- or: '|'
- xor: '^'
Functia pe care va trebui sa o implementati voi va folosi variabilele n (numarul de termeni) si expr (vectorul cu termenii expresiei).
Pentru problema DP or math? partitionam toate subsirurile dupa critieriul paritatii sumei subsirului (cate sunt pare/impare).
Pentru problema expresie booleana partitionam toate parantezarile posibile dupa rezultatul lor (cate dau true/false).
Bonus
Asistentul va alege una dintre problemele din sectiunea Extra.
Extra
Referințe
[0] Capitolul Dynamic Programming din Introductions to Algorithms de către T. H. Cormen, C. E. Leiserson, R. L. Rivest, C. Stein