Laboratorul 07 - Sumatorul Carry-Lookahead

Obiective

Scopul acestui laborator este proiectarea unui sumator Carry-lookahead, care are performanțe mai bune decât sumatorul Ripple-Carry studiat în laboratorul trecut. De asemenea, vom vedea ce este registrul SREG din cadrul unui UAL.

1. Recapitulare

a. Sumatoare multi-bit

În viața reală noi lucrăm cu numere reprezentabile pe mai mulți biți. Totuși, sumatoarele de tip Half-Adder și Full-Adder pot aduna cel mult un bit. Pentru depășirea acestei limitări, laboratorul trecut am implementat un circuit capabil să facă suma numerelor reprezentate pe mai mulți biți.

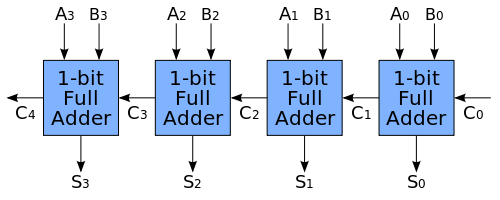
Sumatorul Ripple-Carry

Cel mai simplu circuit este sumatorul ripple-carry care folosind N sumatoare full-adder poate însuma numere pe N biți.

Conectarea lor, prezentată în figura de mai sus, este una foarte simplă: ieșirea C_out a modulului de rang i va fi conectată la intrarea C_in a modulului de rang i+1.

Limitări

Implementarea acestuia este facilă, însă performanța este scăzută. De ce? Deoarece transportul de intrare pentru fiecare sumator complet este dependent de semnalul carry-out din full-adder-ul anterior. Prin structura sa internă: modulul de rang i trebuie să aştepte modulul de rang i-1 sa îşi termine execuția pentru a afla cât este C_{in_i}.

Îmbunătățiri

Cum putem implementa un circuit mai rapid? Eliminând dependența între rang-uri în ceea ce privește bitul de carry. Pentru început aflăm expresia în logică booleană pornind de la tabelul de adevăr al bitului de carry C₁.

A₀	B₀	C₀	C₁
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

Scriem expresia logică corespunzătoare liniilor din tabel pentru care C₁ are valoarea 1:

C₁ = A₀ * B₀ * C₀ + A₀ * B₀ * ~C₀ + ~A₀ * B₀ * C₀ + A₀ * ~B₀ * C₀
C₁ = A₀ * B₀ * (C₀ + ~C₀) + C₀ * (~A₀ * B₀ + A₀ * ~B₀)
C₁ = A₀ * B₀ + C₀ * (A₀ ⊕ B₀)

Dacă generalizăm formula:

C_i+1 = A_i * B_i + C_i * (A_i ⊕ B_i)

Prin urmare, pentru fiecare modul de full-adder, am putea calcula bitul carry de intrare cu cost constant egal cu 1, fără să mai așteptăm propagarea acestuia prin toate celelalte full-adder-e de rang mai mic.

C_out = Generează_biții_carry? SAU Propagă_bitul_de_carry_de_la_rangul_inferior_dacă_nu_e_generat?

2. Prezentare generală

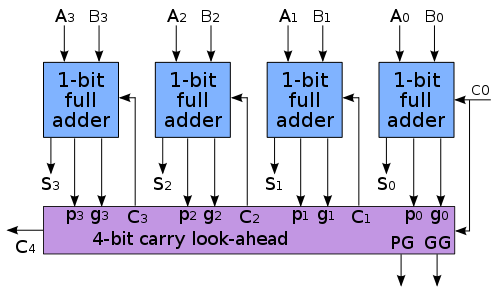
Pentru a reduce timpul necesar unui calcul, proiectanții folosesc sumatorul carry-lookahead.

În sumatorul cu transport anticipat, fiecare adunare pe bit elimină dependenţa de semnalul carry-out anterior şi impune în schimb utilizarea valorilor celor doi operanzi de intrare. El functioneaza prin generarea a două noi semnale (P si G) pentru fiecare rang binar în funcție de starea intrărilor.

G - reprezintă un semnal de generare a unui bit de carry.
P - reprezintă un semnal de propagare a unui bit de carry.

Deci pentru suma a două numere A și B, dacă bitul n din A, împreună cu bitul n din B generează un semnal G, înseamnă că acești biți generează un bit de carry, iar în cazul unui semnal P, bitul de carry de la n-1 (dacă există) este propagat de către biții n pe poziția n+1.

Pornind de la un sumator ripple-carry, pentru fiecare full-adder (i), semnalul carry-out, c(i+1), este setat la 1 dacă una dintre următoarele condiții este adevărată:

A_i = 1 AND B_i = 1

(A_i = 1 OR B_i = 1) AND c_i = 1

am observat că putem calcula semnalul carry-out folosind doar semnalele rangului curent:

c_i+1 = A_i & B_i | c_i & (A_i | B_i) (1)

Pentru un sumator carry-lookahead definim G_i(A_i, B_i) ca fiind predicatul logic care este adevărat atunci când A_i * B_i generează carry (primul caz)

G_i(A_i, B_i) = A_i & B_i

Si P_i(A_i, B_i) ca fiind predicatul logic care este adevărat atunci cand A_i + B_i propagă carry (al doilea caz)

P_i(A_i, B_i) = A_i | B_i

Implementarea bitului de propagare cu XOR

Uneori (dar nu și în laboratorul de față) se folosește și o altă definiție a propagării. Exprimarea lui P_i = A_i + B_i va propaga carry-ul (dacă numai unul dintre A_i și B_i este 1), dar va propaga și atunci când sumatorul generează carry (A_i și B_i sunt ambele 1). Rezultatul final este corect oricum, însă preferăm să nu propagăm atunci când generăm carry. Astfel, putem folosi operatorul XOR, pentru a propaga carry-ul atunci când numai unul dintre biții A_i și B_i este 1, dar nu ambii:

P'_i(A_i, B_i) = A_i ⊕ B_i

Desi OR(prima variantă) e mai rapid decât XOR(a doua variantă), pentru un sumator carry-lookahead pe mai multe nivele e mai avantajos să folosim P'_i(A_i, B_i).

Rescriind ecuația (1) cu P_i si G_i, rezultă:

c_i+1 = G_i | P_i & c_i

Pentru o comparație mai tangibilă a întârzierilor celor 2 sumatoare (ripple-carry și carry-lookahead), puteți folosi aceste 2 simulatoare cu întârziere setabilă pentru porțile folosite (se pot observa întârzieri semnificative ale lui ripple-carry față de carry-lookahead pentru numere reprezentabile pe 32 de biți):

3. Detalii de implementare

Pentru fiecare rang dintr-o secvență binară, sumatorul va determina dacă perechea de biți care trebuie adunată poate genera sau propaga carry. Acest lucru permite circuitului sa “pre-proceseze” cei doi termeni ai adunării pentru a determina transportul înainte de a efectua adunarea propriu-zisă. Apoi, când aceasta are loc, nu va exista nici o întârziere de propagare a carry-ului, ca în cazul unui Ripple Adder. Mai jos aveți un exemplu de calcul al termenilor de propagare și, generare pentru un sumator de 2 biți:

c₁ = G₀ | P₀ & c₀
c₂ = G₁ | P₁ & c₁

Înlocuind c₁ în expresia lui c₂, vom obtine urmatoarele ecuații:

c₁ = G₀ | P₀ & c₀
c₂ = G₁ | P₁ & G₀ | P₁ & P₀ & c₀

Similar, putem generaliza pentru un sumator de 4 biți:

c₃ = G₂ | P₂ & G₁ | P₂ & P₁ & G₀ | P₂ & P₁ & P₀ & c₀

ȘI-ul logic (&) are prioritate față de SAU logic (|)!

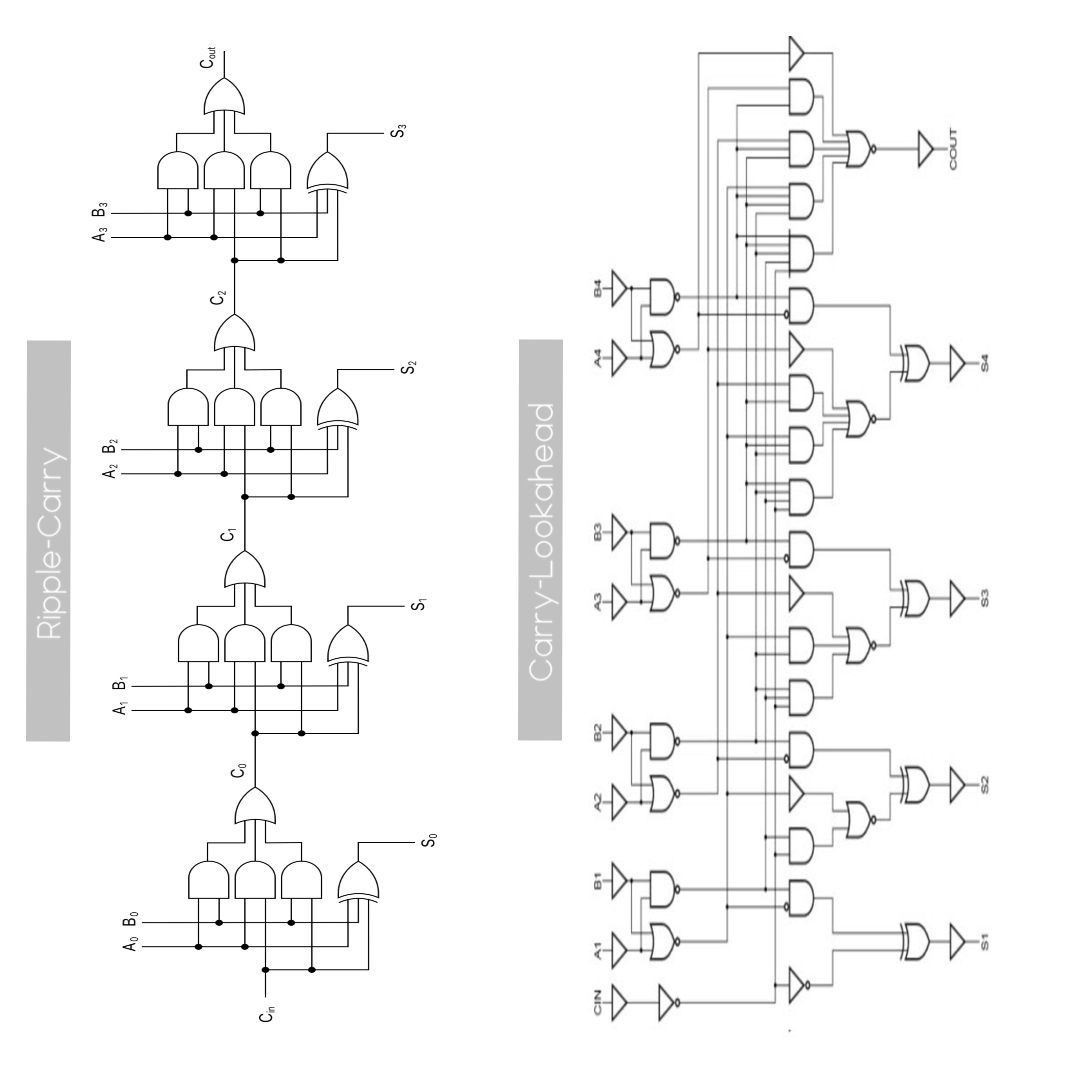
Putem observa că pentru un sumator carry-lookahead cu 4 biți (cel de mai sus), propagarea semnalului de carry până la ieșirea ultimului nivel de adunare necesită trecerea prin 3 porți logice, pe când un sumator ripple-carry necesită trecerea prin 6 porți.

4. Status Register

În urma calculelor făcute de UAL pot apărea anumite situații, precum overflow la adunare/scădere, care este util să fie semnalate în cadrul sistemului. În acest scop procesoarele au un registru de status în care prin setarea unui bit anume este semnalat un anumit eveniment. Cel mai adesea, informațiile din registrul de status (sau Status Register) sunt folosite pentru a modifica fluxul de execuție al programului pe baza instrucțiunilor condiționale.

Spre exemplu, procesorul calculează A + B și dorește să sară la o anumită etichetă dacă rezultatul este 0. UAL va calcula rezultatul lui A + B și va seta bitul Z (Zero) din Status Register dacă rezultatul adunării este 0. Instrucțiunea de salt JZ (jump zero) verifică bitul Z din Status Register și sare la eticheta data dacă bitul este 1, altfel execută instrucțiunea imediat următoare.

În cadrul x86 Status Register se numește FLAGS și are 16 biți. El are o extensie de 32 de biți numită EFLAGS. Biții din cele două registre au următoarea semnificație:

Un exemplu mai simplu este registrul de status pentru Atmega324 (AVR în general), care se numește SREG și are 8 biți:

În ambele registre de status prezentate mai sus se regăsesc o serie de biți de interes pentru UAL:

CF sau C (carry flag) este setat pe 1 când operația executată pe UAL are carry.
ZF sau Z (zero flag) este setat pe 1 când rezultatul operației de pe UAL este 0.
N (negative) este setat pe 1 când rezultatul operației de pe UAL este un număr negativ (bitul de semn al rezultatului este 1).
OF sau V (overflow flag) este setat pe 1 când operația executată pe UAL produce overflow, mai exact există 2 cazuri:
- dacă adunăm 2 numere pozitive și bitul de semn al rezultatului este 1 (rezultatul este număr negativ)
- dacă adunăm 2 numere negative și bitul de semn al rezultatului este 0 (rezultatul este număr pozitiv)

TL;DR

Sumatorul Ripple-Carry calculează valoarea unui bit i din adunare doar după ce au avut loc calculele pentru toți biții de la 0 la i - 1, deci calculul pentru fiecare bit are loc secvențial.

Sumatorul Carry-Lookahead calculează valoarea unui bit i independent de calculele pentru ceilalti biți (în paralel) folosind formulele:
- G_i(A_i, B_i) = A_i & B_i
- P_i(A_i, B_i) = A_i | B_i
- c_i+1 = G_i | P_i & c_i
Există un compromis între viteză și cost (complexitate hardware)
Status Register: Registru de flag-uri: ZF/Z - Zero, CF/C - Carry, N - Negative, OF/V - Overflow
Setate de UAL în momentul producerii unor evenimente.

Exerciții

Pentru fiecare dintre exerciții va trebui să faceți atât implementarea cât și simularea cu seturi de date relevante. (minim 3 cazuri de test)

Task 00 (4p) Implementați un sumator carry-lookahead pe 4 biți.

Task 01 (2p) Implementați un scăzător carry-lookahead pe 4 biți, pornind de la punctul precedent.

Task 02 (4p) Implementați un sumator pe 16 de biți folosind modulul carry-lookahead deja implementat și logica sumatorului ripple-carry.

Task 03 (bonus - 2p) Implementați un sumator/scăzător carry-lookahead pe 4 biti cu ajutorul plăcii de laborator. Interacțiunea cu modulul se va face astfel:

Intrări:
- operandul A → 4 switch-uri
- operandul B → 4 switch-uri
- buton1 → buton pentru validarea operanzilor
- buton2 → buton pentru operația de adunare
- buton3 → buton pentru operația de scădere
- buton reset
Ieșiri:
- cele 8 leduri → pentru afisarea progresului (o_r_leds)
- afisajul cu 7 segmente → pentru afișarea rezultatului (l_r_message)
Mod de operare:
- STATE_INITIAL:
  - se introduc valorile celor doi operanzi folosind switch-urile
  - pe cele 8 leduri se va afișa valoarea PROGRESS_NONE
  - pe afișajul cu 7 segmente se va afișa valoarea unuia dintre operanzi
- la apăsarea lui buton1:
  - se salvează în memorie valoarea operanzilor
  - se trece în starea STATE_OP_READ
- STATE_OP_READ:
  - pe cele 8 leduri se va afișa valoarea PROGRESS_BOTH_OPERANDS
  - pe afișajul cu 7 segmente se va afișa mesajul APAS (PRESS_MESSAGE)
- la apăsarea lui buton2 sau buton3:
  - se trece în starea STATE_RESULT_SELECT
- STATE_RESULT_SELECT
  - pe cele 8 leduri se va afișa valoarea PROGRESS_RESULT
  - pe afișajul cu 7 segmente se va afișa:
    - mesajul APAS (PRESS_MESSAGE), dacă nu este apăsat nici buton2, nici buton3
    - suma celor doi operanzi din memorie, dacă este apăsat buton2
    - diferența celor doi operanzi din memorie, dacă este apăsat buton3
  - suma și diferența vor fi afișate în zecimal
- pentru introducerea altor valori pentru operanzi se va apăsa butonul de reset
- pentru a realiza operațiile veți folosi modulele create la exercițiile anterioare