Scopul acestui laborator este proiectarea unor module ce implementează operații aritmetice. În acest laborator vom implementa sumatoare simple și le vom examina performanțele.

Cuvintele calculatoarelor sunt compuse din biți, deci o reprezentare facilă este în numere binare. Numărul de biți din care este compus un cuvânt determină gama de valori reprezentabilă în acel cuvânt. Spre exemplu, un cuvânt de 32 de biți poate conține valori între 0 și 2³² - 1 = 4.294.967.295 (desigur, am considerat numărul ca fiind fără semn).

De asemenea, pentru a reprezenta numere negative putem folosi primul bit dintr-un cuvânt ca bit de semn. Astfel un cuvânt cu primul bit 0 este considerat număr pozitiv, iar un cuvânt cu primul bit 1 este considerat negativ. Numerele negative sunt reprezentate în cod complementar lui 2. In acest caz, un cuvânt de 32 de biți poate conține valori între -2³¹ și 2³¹ - 1 ([-2.147.483.648, 2.147.483.647]).

Un sumator este un circuit digital ce realizează suma a două numere. În calculatoarele moderne ele se găsesc nu numai în unitatea aritmetică-logică (UAL) ci și în alte unități ale procesorului, fiind folosite pentru a calcula adrese, indici, etc.

Un half-adder este un circuit care realizează suma a doi operanzi pe un singur bit. Intrările sale sunt A și B, cei doi operanzi. El generează la ieșire două semnale: S (suma) si C (carry - transportul către următorul rang). Tabela de adevăr pentru un half-adder este prezentată în figura 3.1.

Fig 3.1: Tabela de adevăr pentru un half-adder

Un full-adder este un circuit care realizează suma a doi operanzi ținând cont și de transportul din rangul inferior. Intrările sale sunt A, B (cei doi operanzi) și C_in (transportul de la rangul inferior). El generează la ieșire doua semnale: S (suma) și C_out (carry out - transportul către rangul următor). Tabela de adevăr pentru un full-adder este prezentată în figura 3.2.

Figura 3.2: Tabela de adevăr pentru un full-adder

Un full-adder se poate implementa folosind 2 half-addere:

Cum în practică vom avea nevoie de numere mai mari decât 1, acestea vor fi reprezentate pe mai mulți biți. În acest caz avem o problemă: sumatoarele noastre nu pot aduna decât maxim un bit! Pentru a rezolva problema trebuie să creăm un circuit care să facă suma numerelor reprezentate pe mai mulți biți.

Un astfel de circuit, și cel mai simplu, este sumatorul ripple-carry. Pentru a construi un astfel de sumator pe n biți avem nevoie de fie n sumatoare full-adder (dintre care primul va avea intrarea C_in legată la 0 întotdeauna), fie de n-1 sumatoare full-adder și un half-adder (care va înlocui NUMAI acel prim full-adder fără C_in).

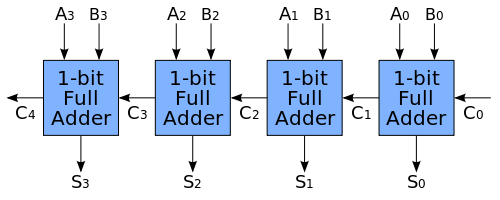
Conectarea lor, prezentată în figura 3.3, este una foarte simplă: ieșirea C_out a modulului de rang i va fi conectată la intrarea C_in a modulului de rang i+1. Acest fapt ne bucură în faza de proiectare, fiindcă nu avem mult de lucru, însă un astfel de sumator este încetinit de faptul că modulul de rang i trebuie să aştepte modulul de rang i-1 sa îşi termine executia pentru a afla cât este C_in, iar cel de rang i-1 la rândul său trebuie să îl aștepte pe cel de rang i-2 s.a.m.d.

Figura 3.3: Un sumator ripple-carry pe 4 biți

• Cuvintele calculatorului sunt compuse din biți, prin urmare, cuvintele sunt doar niște valori.
  • Convenție (Complement față de 2):
    • pozitive - primul bit este 0
    • negative - primul bit este 1
• Sumator = circuit digital care realizează suma a două numere
  • Half-adder = realizează suma a doi operanzi pe un singur bit
  • Full-adder = realizează suma a doi operanzi pe un singur bit ținând cont și de transportul din rangul inferior
  • Ripple-carry = sumator pe n biți realizat din n sumatoare 'full-adder' cascadate
    • C_{in⁽ⁱ⁺¹⁾} = C_out⁽ⁱ⁾
    • C_in⁽⁰⁾ = 0

1. (4p) Implementați un half-adder și un full-adder fără să folosiți operatorul '+' din Verilog.
   1. (2p) Implementarea half-adder se va face la oricare dintre din următoarele nivele:
      • la nivel structural
      • la nivel flux de date
      • la nivel procedural
   2. (2p) Implementarea full-adder se va face utilizând două instanțe ale half-adder-ului implementat la subpunctul anterior.
2. (2p) Implementați un sumator ripple-carry pe 8 biți.
   • !!! Pentru implementare folosiți modulele de la punctul precedent.
3. (2p) Implementați un scăzător pe 8 biti, pornind de la modulul de la punctul precedent.
4. (4p) Implementați un sumator/scăzător pe 8 biți cu ajutorul plăcii de laborator.
   1. Caracteristici:
      1. 2 operanzi pe 8 biţi
      2. Afişare operanzi şi rezultat pe afişajul cu 7 segmente
      3. Afişare progres pe cele 8 LED-uri
   2. Mod de operare:
      1. Preluare operand 1 → prin apăsarea unui 'push-button'
      2. Preluare operand 2 → prin apăsarea aceluiaşi 'push-button'
         • !!! Până la apăsarea butonului, pe afişajul cu 7 segmente va fi afişată valoarea operandului
      3. Afişare:
         • rezultat → dacă este ţinut apăsat butonul corespunzător unei operaţii
         • 'APAS' → dacă nu este apăsat niciun buton
      4. La apăsarea butonului de reset, circuitul se întoarce la preluarea primului operand
   • Citiţi comentariile din modul şi urmăriţi TODO-urile!

• Scheletul de laborator

• Datasheet Digilent Nexys A7
• Schema Digilent Nexys A7

• Generate in verilog
• Ripple Carry Adder Simulator