Responsabili:

• Dănuţ Matei
• Luca Istrate

Data publicării : 27 aprilie, ora: 01:05

Deadline: 19 mai, ora 23:55

• 1 mai, ora 00:25 - adăugat schelet + checker
• 10 mai, ora 17:50 - adăugat în arhivă fișier necesar pentru partea de coding style;
• 10 mai, ora 18:20 - mică clarificare în exemplul de possible_erasures() din secţiunea Metode de implementat
• 16 mai, ora 21:15 - am adăugat tema și pe vmchecker

În urma realizării acestei teme:

• veţi exersa lucrul colaborativ în echipe de câte doi
• veţi putea lucra cu elemente colaborative pentru uşurarea muncii (e.g git pentru versionare de cod)
• veţi învăţa să lucraţi cu structuri arborescente
• vă veţi acomoda cu gândirea şi implementarea de funcţii recursive

Un graf existenţial este o formă de reprezentare vizuală a expresiilor logice, propusă de Charles Sanders Peirce în 1882. Avantajul acestora este faptul că oferă o alternativă vizuală la inferenţa prin formule logice matematice.

Scopul temei este realizarea unui program care verifică dacă există un raţionament valid care poate ajunge de la o ipoteză dată la o concluzie dată şi, în caz afirmativ, să afişeze transformările intermediare implicate în acest raţionament.

Sintaxa unui graf existenţial este formată din 3 tipuri de entităţi:

• Foaia de aserţiune - o suprafaţă imaginară pe care se vor trece restul elementelor;
• Litere, simbolizând propoziţii logice
• Tăieturi - linii circulare închise ce reprezintă negarea elementului / grupului de elemente pe care îl conţin

În continuare, vom considera că foaia de aserţiune este unică per desen.

Toate elementele care sunt trecute direct pe foaia de aserţiune se consideră a fi simultan adevărate. Astfel, dacă propoziţiile P , Q şi R sunt trecute pe foaia de aserţiune, atunci propoziţia “P şi Q şi R” este adevărată.


Să analizăm cum ar arăta o serie de propoziţii sub formă de grafuri existenţiale:


P && Q-literele P şi Q sunt trecute direct pe foaia de aserţiune. Distanţa şi poziţia lor nu au nicio relevanţă pentru valoarea lor de adevăr.





!P-deoarece litera P este înconjurată de o tăietură, atunci valoarea de adevăr a propoziţiei este negată





P ⇒ Q, echivalentă logic cu “!(P and !Q)”-litera Q este înconjurată de o tăietură, această nouă formaţiune e trecută lângă litera P, iar ambele sunt în continuare înconjurate de o tăietură comună



P || Q, echivalentă logic cu “!(!P && !Q)”-foarte similar cu exemplul c)




Astfel, un graf poate fi:

• o propoziţie
• o tăietură, împreună cu toate elementele pe care le înconjoară
  

Definim nivelul pe care se află un subgraf drept un număr întreg egal cu numărul de tăieturi de care e înconjurat subgraful. Astfel, un subgraf care se află pe foaia de aserţiune se află pe nivelul 0, unul înconjurat de o tăietură se află pe nivelul 1 etc.

Alte exemple:


Noţiunea de nivel poate fi înţeleasă mai intuitiv dacă ne imaginăm fiecare tăietură ca pe un disc circular pe care se aşază restul elementelor conţinute de aceasta. Spre exemplu, pentru propoziţia S && !(!(P && !Q) && R), graful existenţial ar arăta în felul următor:


Dacă ar fi să ne imaginăm cum ar arăta acest graf privit dintr-un plan lateral, am vedea ceva similar cu:

Ţinând cont de această structură ierarhică, am putea încerca să reprezentăm un graf existenţial sub formă de arbore. Astfel, rădăcină va reprezenta foaia de aserţiune, iar fiii acesteia vor fi subgrafurile de pe nivelul 0. Un nod diferit de rădăcină va reprezenta fie o propoziţie (caz în care nu va avea fii), fie o tăietura (caz în care va avea drept fii subgrafurile pe care le încercuieşte).

Spre exemplu, un arbore echivalent pentru exemplul precedent ar arăta în felul următor:


Se poate observa o corespondenţă între nivelul în graful existenţial şi nivelul în arborele echivalent:

Sarcina voastră va fi să realizaţi operaţii pe un asemenea arbore pentru a implementa o parte din regulile de inferenţă care vor fi prezentate în continuare.

Pentru ca sistemul de grafuri existenţiale să fie echivalent cu logica propoziţională, avem nevoie de 5 reguli de inferenţă:

• Insertion - orice subraf poate fi inserat pe un nivel impar
• Erasure - orice subgraf poate fi şters de pe un nivel par
• Double Cut - o pereche de tăieturi care nu au nimic între ele poate fi eliminată (din acelaşi motiv pentru care !!P este echivalent cu P)
• Deiteration - Fie n un nod n care are drept fiu graful k. Graful k poate fi şters din orice alt descendent al nodului n.
• Iteration - Fie n un nod care are drept fiu graful k. Graful k poate fi introdus drept fiu al oricărui alt descendent al nodului n.

Ceea ce ne dorim să facem este ca, dându-se o ipoteză şi o concluzie, să verificăm dacă există o demonstraţie, adică o modalitate de a ajunge la concluzie printr-o serie de transformări asupra ipotezei.

Totuşi, o modalitate mai simplă pentru a demonstra propoziţia P ⇒ Q (ipoteză implică concluzie) este să folosim principiului reducerii la absurd, demonstrând că !(P ⇒ Q) duce la o contradicţie. P ⇒ Q este echivalent cu \ !(P && !Q), deci !(P ⇒ Q) va fi echivalent cu !!(P && !Q), adică P && !Q.

Astfel, pornim cu P && !Q pe foaia de aserţiune (unde P reprezintă propoziţiile din ipoteză, iar Q propoziţiile din concluzie) şi, folosind regulile de inferenţă, încercăm să ajungem la o contradicţie (în general, un graf de tipul \ K && !K).

Acest proces este unul de simplificare a structurii grafului, deci în simularea lui va trebui să implementaţi numai regulile 2, 3 şi 4 (Erasure, Double Cut şi Deiteration). Din cauza faptului că, la un pas oarecare, alegerea regulii următoare nu este deterministă, vom avea nevoie de o strategie de tip backtracking (implementată deja în checker).

În scheletul de cod şi în testarea operaţiilor ne-am folosit de reprezentarea serializată a arborilor echivalenţi. Câteva exemple ale acestei serializari sunt:

Conversia între structura internă a unui arbore echivalent şi reprezentarea serializată, precum şi conversia inversă, au fost deja implementate în scheletul de cod. Motivul pentru care trebuie să înţelegeţi această reprezentare e pentru a putea înţelege input-ul şi output-ul şi pentru a vă putea crea teste custom.

1.





2.

Exemplu incorect:






Este incorect deoarece un subgraf poate fi deiterat doar din fiii nodului curent

1.






2.

Exemplu incorect:






Este incorect deoarece un subgraf poate fi şters numai dacă se află pe un nivel par.

• întoarce poziţiile pe care am putea realiza operaţii de double cut

Exemplu:

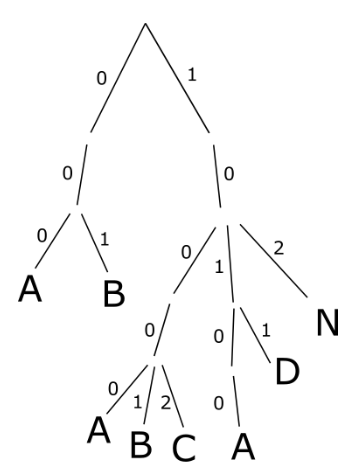
  ([[A, B]], [[[[A, B, C]], [[A], D], N]])
  
  0
  1
  1 0 0

Putem aplica double cut pe fiul 0 al rădăcinii: [[A, B]]

Pe fiul 1: [[[[A, B, C]], [[A], D], N]]

Sau selectăm fiul 1 al rădăcinii, apoi fiul 0 al acestuia, apoi fiul 0 al acestuia din urmă, deci pe: [[A, B, C]]

• realizează operaţia de double cut în poziţia primită ca argument (care se presupune că e validă)
• L este o listă de indecşi ce indică numărul fiului care trebuie ales la fiecare pas.

• întoarce poziţiile unde am putea aplica operaţii de deiteration

Exemplu:

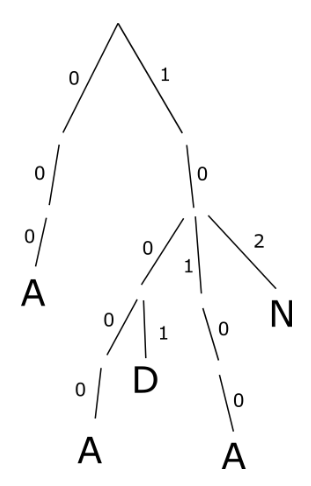
  ([[A]], [[[[A], D], [[A]], N]])
  
  1 0 1

Putem deitera doar fiul [1 0 1]: [[A]], obţinând:

([[A]], [[[[A], D], N]])

• realizează operaţia de deiteration la poziţia specificată de L
• L este o listă de indecşi care indică numărul subgrafului ce trebuie selectat la fiecare pas
• pentru un nod cu n copii, primii k fii sunt fii-tăieturi, iar următorii până la n sunt fii-frunză (atomi)
• dacă trebuie să selectăm un nod n mai mare decât k, înseamnă că este frunză (atom) şi vom selecta atomul cu numărul n-k

• întoarce poziţiile unde am putea aplica operaţii de erase

Exemplu:

   ([[A]], [[[[A], D], [[A]], N]]) 
    
   0 
   1 
   1 0 0 
   1 0 1 
   1 0 2 
    

Putem şterge fiul 0 al rădăcinii: [[A]]

Fiul [1]: [[[[A], D], [[A]], N]]

Fiul [1 0 0]: [[A], D]

Fiul [1 0 1]: [[A]]

Fiul [1 0 2]: N

• similar cu operaţia deiterate

• schelet_checker.zip
• vmchecker

• 80 puncte obținute pe testele de pe vmchecker. Condiții pentru obținerea punctajului total:
  • fără memleak-uri
  • fără erori de valgrind
• 10 puncte: README
• 10 puncte pentru coding style, proporțional cu punctajul obținut pe teste

Q: Ce se poate folosi din STL?

A: Orice, atât timp cât respectaţi declaraţiile funcţiilor pe care trebuie să le implementaţi

Q: Ambii membri ai echipei obţin acelaşi punctaj?

A: Nu neapărat; cei doi membri ai echipei pot să obţină punctaje diferite dacă volumul de muncă depus de unul nu este comparabil cu cel depus de celălalt

Q: E suficientă o singură submisie per pereche?

A: Da. Trebuie să specificaţi în README ambii membri ai echipei.