Responsabili

• Andrei Pîrlea
• Ștefan-Teodor Dascălu

În urma parcugerii acestui laborator, studentul va:

• avea cunoștințele de baza despre ArrayList și LinkedList
• putea implementa propria listă simplu înlănțuită
• putea compara o listă înlănțuită cu un vector

Cum ați învățat la PC și în laboratorul anterior, un vector este o colecție liniară și omogenă de date. În cazul alocării dinamice (care va fi și modul predominant în care vom lucra cu structurile de date), această zonă are o capacitate care se poate modifica (mări sau micșora) în funcție de diferite criterii de redimensionare (de exemplu: putem dubla capacitatea vectorului dacă ajungem la 75% din capacitatea sa curentă și putem înjumătăți capacitatea dacă vectorul esti plin în proporție mai mică de 25%). Obținem astfel mai multă memorie liberă, însă, trebuie să plătim prețul overhead-ului dat de realocarea array-ului.

O listă înlănțuită (LinkedList) reprezintă o structură de date liniară și omogenă. Spre deosebire de vector, lista înlănțuită nu își are elementele într-o zonă contiguă de memorie, ci fiecare element (nod al listei) va conține pe langă informația utilă și legătură către nodul următor (listă simplu înlănțuită), sau legături către nodurile vecine (listă dublu înlănțuită). Alocând dinamic nodurile pe măsură ce este nevoie de ele, practic se pot obține liste de lungime limitată doar de cantitatea de memorie accesibilă programului.

O listă înlănțuită are întotdeauna cel puțin un pointer: head. După cum spune și numele, el reprezintă capul listei, începutul ei. head va indica mereu către primul element al listei. Un alt pointer ce poate fi folosit pentru a facilita lucrul cu lista este tail, care, după cum spune și numele, reprezintă coada listei, sfârșitul ei, el indicând către ultimul element al listei. Pe lângă cei doi pointeri precizați, este recomandat să avem salvată și lungimea listei.

În concluzie, putem defini o listă în cod astfel:

struct Node {
    void* data; // pointer void pentru a utiliza orice tip de date
    ...
};
 
struct LinkedList {
    struct Node* head;
    ...
};

Asupra unei liste înlănțuite ar trebui să putem executa urmatoarele operații:

• void add_nth_node(struct LinkedList* list, int n, void* new_data); adaugă pe poziția n în listă elementul new_data. Adăugarea presupune modificarea câmpului next al nodului în urma căruia se va adăuga noul nod, cât și a câmpului next al nodului adăugat pentru a face legăturile necesare ca lista sa funcționeze corect. Dacă nodul este adăugat pe prima poziție, atunci el va deveni head-ul listei, iar dacă este adăugat pe ultima poziție, el va deveni tail-ul listei. Complexitate: O(n). Dacă se adaugă elementul în capul sau coada listei, se obține o complexitate mai bună: O(1).

• struct Node* remove_nth_node(struct LinkedList* list, int n); șterge și întoarce al n-lea element al listei. Operația presupune modificarea listei astfel încât între nodurile vecine celui eliminat să se refacă legaturile pentru a permite listei să funcționeze în continuare. Daca nu există un nod următor, head va deveni NULL, iar lista va fi goală. Dacă nodul eliminat era head-ul listei, atunci succesorul său îi va lua locul. Analog pentru ultimul nod, însă în această situație, nodul precedent devine tail. Atentie! Funcția doar returnează nodul eliminat din listă, deci rămâne de datoria voastră să eliberați memoria ocupată de nodul obținut în urma apelului funcției. Complexitate: O(n). Dacă se șterge primul nod, se obține o complexitate mai bună: O(1). Aceeași complexitate se obține și dacă lista este dublu înlănțuită și se șterge ultimul nod.

• int get_size(struct LinkedList* list); întoarce numărul curent de elemente stocate în listă. Complexitate: O(1)

Există doua mari tipuri de liste înlănțuite: liniare și circulare.

Listele liniare se numesc astfel deoarece ele au un caracter liniar: încep undeva și se termină altundeva, fără a fi o legatură înapoi la începutul listei. Așadar, într-o listă liniară, câmpul next al ultimului element va indica spre NULL. Dacă nodurile au legatură și spre elementul anterior, atunci câmpul prev al primului element va indica tot spre NULL.

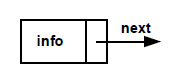
În acest laborator vom discuta doar despre listele simplu înlănțuite. Cum am aflat anterior, un nod al unei liste simplu înlănțuite conține informația utilă și o legătură către nodul următor.

Putem reprezenta în cod acest nod astfel:

struct Node {
    void* data;
    struct Node* next;
};

Îmbinând informațiile despre listele liniare și particularitățile listei simplu înlănțuite, putem reprezenta grafic o lista simplu înlănțuită astfel:

Primul şi ultimul nod sunt legate împreună. Pentru a parcurge o listă circular înlănţuită se începe de la oricare nod şi se urmăreşte lista prin aceasta direcţie aleasă până când se ajunge la nodul de unde s-a pornit parcurgerea (lucru valabil şi pentru listele circulare dublu-înlănţuite).

Fiecare nod are o singură legatură, similar cu listele liniare simplu-înlănţuite, însă, diferenţa constă în legătura aflată după ultimul nod ce îl leagă pe acesta de primul nod. La fel ca şi în listele liniare simplu-înlănţuite, nodurile noi pot fi inserate eficient numai dacă acestea se află după un nod care are referinţe la acesta. Din acest motiv, este necesar să se menţină numai o referinţă către ultimul element dintr-o listă circulară simplu-înlănţuita, căci aceasta permite o inserţie rapidă la nodul de început al listei, şi de asemenea, permite accesul la primul nod prin legatura dintre acesta şi ultimul nod.

Scheletul de laborator

Enunțurile problemelor le găsiți pe Lambda Checker, aici. Tot acolo veți și încărca soluțiile voastre.

Această secțiune nu este punctată și încearcă să vă facă o oarecare idee a tipurilor de întrebări pe care le puteți întâlni la un job interview (internship, part-time, full-time, etc.) din materia prezentată în cadrul laboratorului.

1. Implementați o funcție de ștergere a duplicatelor dintr-o listă simplu înlănțuită sortată.
2. Implementați o funcție de detectare (+ înlăturare) a unui ciclu într-o listă simplu înlănțuită.
3. Găsirea celui de-al k-lea nod de la sfârșit spre început într-o listă simplu înlănțuită.

Și multe altele…

1. Linked list visualization
2. CLRS - Introduction to Algorithms, 3rd edition, capitol 10.2 - Linked lists