Laborator 9 - Arbori generici. Trie
Responsabili
Obiective
În urma parcurgerii articolului, studentul va fi capabil să:
- înţeleagă noţiunea de arbore generic
- înţeleagă noţiunea şi structura unui trie
- construiască, în limbajul C, un trie
- utilizeze un trie
Arbori generici
Până acum am studiat arbori binari, în cadrul cărora un nod avea cel mult 2 fii. Generalizarea arborilor binari este reprezentată de arborii generici, denumiți și k-ary trees, întrucât, în cadrul acestora, un nod poate avea cel mult k fii.
În exemplul de mai sus, putem observa un 6-ary tree, unde nodurile pot avea cel mult 6 fii - observăm astfel noduri cu 0, 1, 2 sau 6 fii.
Schelet minimal de structură de arbore generic:
- generic_tree.h
typedef struct g_tree_t g_tree_t; struct g_tree_t { g_node_t *root; }; typedef struct g_node_t g_node_t; struct g_node_t { void *value; g_node_t **children; int n_children; };
De ce trie?
O particularizare a arborilor generici este dată de Trie. Cunoscut și sub numele de arbore de prefixe (prefix tree), trie-ul este un arbore de căutare care permite operații de inserare și căutare de elemente in complexitate O(L) (L - lungimea cheii).
De obicei trie-ul este folosit pentru a stoca string-uri și valori asociate acestora. Pe parcursul semestrului am studiat alte 2 structuri de date care pot efectua aceleași operații: hashtable-ul si arborele binar de căutare. De ce am studia înca o structură de date care poate realiza aceleași operații? Să comparăm Trie-ul cu:
- ABC: Trie-ul poate insera și căuta elemente in O(L), având o complexitate mai bună decât un arbore binar de căutare balansat O(logN) (ținând cont că în general lungimile cuvintelor sunt mult mai mici decât numărul de cuvinte stocate).
- Hashtable: Pentru toate operațiile sale, trie-ul are o performanță comparabilă (uneori mai bună) față de un hashtable.
- Față de ambele structuri, trie-ul permite operații de căutare mai avansate, putând efectua căutari eficiente după prefix sau pentru cuvinte cu un număr de caractere lipsă sau greșite (autocomplete).
Care este dezavantajul acestei structuri?
- Memoria utilizată variază în funcție de prefixele pe care le au in comun, însă în cazul cel mai defavorabil, numărul de noduri este egal cu suma lungimilor cheilor.
Ce este un trie?
Un trie este o structură de tip arbore care reține asocieri de tip cheie - valoare. Cheia este reprezentată în general de un cuvânt sau un prefix al unui cuvânt, dar poate fi orice listă ordonată (ex: reprezentarea binară a numerelor - bitwise trie)
Rădăcina utilizează pe post de cheie un string vid (””). Diferența de lungime dintre cheia asociată unui nod și cheile copiilor săi este de 1. Astfel, copiii rădăcinii sunt noduri cu chei de dimensiune 1, iar copiii acestora au chei de dimensiune 2, etc.
În concluzie, putem spune că pentru un nod aflat la distanța k de radacină, acesta are o cheie de lungime k. De asemenea, dacă nodul n1 este strămoș al lui n2 atunci cheia asociată lui n1 este prefix al cheii asociate lui n2.
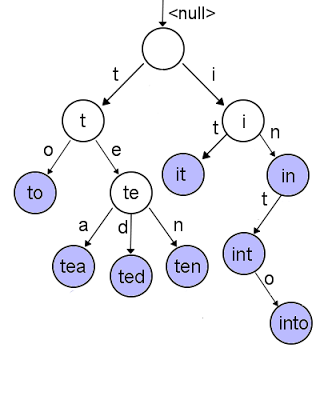
Puteți observa în desenul de mai jos cum arată un trie. De observat că nodurile ce conțin valori sunt colorate cu albastru (nodurile corespunzătoare cheilor “in” și “int” conțin și ele valori, chiar dacă nu sunt noduri frunză)
În desenul de mai sus, trie-ul poate fi asimilat cu implementarea unui dicționar (spre exemplu: DEX; cu intrări de forma <cuvânt : definiția cuvântului>), unde nodurile pot fi privite în felul următor:
// "" reprezintă șirul vid "" : "" t : "" i : "" "to" : "expressing motion in the direction of (a particular location)." "te" : "" "it" : "used to refer to a thing previously mentioned or easily identified." "in" : "expressing the situation of something that is or appears to be enclosed or surrounded by something else." "tea" : "a hot drink made by infusing the dried crushed leaves of the tea plant in boiling water." "ted" : "turn over and spread out (grass, hay, or straw) to dry or for bedding." "ten" : "equivalent to the product of five and two; one more than nine; 10." "int" : "interior." "into" : "expressing movement or action with the result that someone or something becomes enclosed or surrounded by something else."
Implementare
Fiind un arbore, trie-ul va respecta formatul standard al acestei structuri de date, însa cheia nu este reținută în mod explicit. Fiecare nod reține un vector cu fiii săi.
- trie.h
typedef struct trie_node_t trie_node_t; struct trie_node_t { /* Value associated with key (set if end_of_word = 1) */ void* value; /* 1 if current node marks the end of a word, 0 otherwise */ int end_of_word; trie_node_t** children; int n_children; }; typedef struct trie_t trie_t; struct trie_t { trie_node_t* root; /* Number of keys */ int size; /* Generic Data Structure */ int data_size; /* Trie-Specific, alphabet properties */ int alphabet_size; char* alphabet; /* Callback to free value associated with key, should be called when freeing */ void (*free_value_cb)(void*); /* Optional - number of nodes, useful to test correctness */ int nNodes; };
În cadrul implementării din laborator, fiecare nod conține un vector de dimensiunea alfabetului, reprezentând copiii nodului; iar cheile vor conține numai litere mici al alfabetului englez. Poziția unui nod in vectorul părintelui său este dată de poziția în alfabet a literei prin care se diferențiază de cheia parintelui său. În exemplul de mai jos, nodul cu cheia “the” este pe a 5-a poziție in vectorul de copii al nodului cu cheia “th”, deoarece 'e' este a 5-a litera din alfabet.
Deși am spus că nodul cu cheia ”the” este pe a 5-a poziție în vectorul de copii al nodului cu cheia ”th”, acesta pare, conform desenului de mai sus, să fie doar cel de-al doilea copil al nodului ”th”. Motivul este că ”th” reține o listă cu cei 26 de potențiali fii, însă 23 dintre aceștia sunt nuli, în vreme ce doar 3 dintre aceștia există (”a”, ”e”, ”i”).
Căutare
În cazul în care cheia are lungime 0, se reține valoarea asociată nodului și se întoarce true daca nodul curent reprezintă sfârșit de cuvânt, altfel se apelează recursiv metoda search pe nodul care continuă cheia părintelui său cu prima litera a cuvântului primit ca parametru.
Pseudocod
search(key, node) {
if key == ""
// The value of the node is the searched one
return node->value
nextNode = child corresponding to the first letter of the key
if nextNode does not exist
return NULL
return search(key without first letter, nextNode)
}
Inserare
Dacă lungimea cheii este 0, am ajuns la nodul a cărui cheie se vrea a fi inserată. Altfel, se apelează recursiv metoda insert pe nodul a cărui cheie diferă de cheia părintelui său prin prima literă a cuvântului primit ca parametru.
Pseudocod
insert(node, key, value) { // Key is the rest of the initial key to be processed
if length of key == 0
node->data = value
node->end_of_word = true
return
nextNode = child corresponding to the first letter of the key
if nextNode does not exist
create nextNode
node->n_children++
nNodes++
insert(nextNode, key without first letter, value)
}
Ștergere
Metoda întoarce true dacă nodul poate fi șters de către părinte, fiindcă nu este prefixul vreunui cuvânt inserat și fals altfel. Dacă nodul curent este cel ce trebuie șters, se șterge valoarea asociată. În caz contrar, se apelează recursiv metoda remove pe nodul a cărui cheie are ca ultimă literă prima litera a cuvântului primit ca parametru.

În desenul de mai sus, nodurile roșii reprezintă nodurile cu end_of_word = true (cuvinte integrale, de sine stătătoare, adică dacă inserăm ”Mihai” in Trie, doar nodul cu ”Mihai” va avea end_of_word = true, în vreme ce ”M”, ”Mi”, ”Mih”, ”Miha” vor avea end_of_word = false).
Să facem o scurtă trecere prin cele 3 operații din desen:
- “aa”: ”aa” reprezintă un cuvânt (are end_of_word = true), însă are copii (”aa”→n_children > 0), adică reprezintă un prefix pentru alte cuvinte inserate anterior in Trie. Astfel, pur și simplu flag-ul de end_of_word de pe nodul ”aa” este trecut la false.
- “aacx”: ”aacx” reprezintă un cuvânt, și nu are copii, deci se vor șterge nodurile recursiv, de jos în sus - de la ”x” până la primul nod întâlnit (iarăși, de jos în sus, întrucât revenim din recursivitate) ce are copii (cel de-al doilea ”a” din ”aacx”) sau are end_of_word = true.
- “aab”: similar ca mai sus.
Pseudocod
remove(node, key) {
if length of key == 0
free value
if node->end_of_word == true
node->end_of_word = false
// if n_children > 0, then this node marks a prefix of an already existing key, so we shouldn't free it yet
return node->n_children == 0
// remove was called on a key that doesn't exist
return false
nextNode = child corresponding to the first letter of the key
if nextNode exists and remove(nextNode, key without first letter) == true
delete nextNode
node->n_children--
nNodes--
if node->n_children == 0 and node->end_of_word == false
// second condition is mandatory because an intermediary node could mark a valid key AND a prefix of the
// key we are currently deleting at the same time
return true
return false
}
Exerciții
1) [7p] Implementarea Trie-ului
Interviu
Arborii generici si in special trie sunt structuri de date intalnite des la interviuri, in special la companii mari din afara precum Google, Facebook, Amazon, etc.
- Cum ați implementa funcționalitatea de auto-complete?
- Cum ați sorta eficient un array de șiruri de caratere?
- Cum ati organiza ierarhic angajatii dintr-o companie?
- Cata memorie foloseste un nod din Trie? Cum putem optimiza complexitatea spatiala (memoria) unui Trie?