Responsabili:

• Mihai Neacşu
• Cosmin Petrişor

În urma parcurgerii acestui laborator, studentul va fi capabil să:

• înţeleagă diferitele moduri de reprezentare a arborilor;
• definească proprietăţile structurii de heap;
• implementeze operaţii de inserare, ştergere şi căutare care să păstreze proprietatea de heap;
• folosească heap-ul pentru a implementa o metodă de sortare eficientă.

În laboratorul precedent am considerat arborii binari ca fiind o înlănţuire de structuri, legate între ele prin pointeri la descendenţii stâng, respectiv drept. Această reprezentare are avantajul flexibilităţii şi a posibilităţii de a creşte sau micşora dimensiunea arborelui oricât de mult, cu un efort minim. Cu toate acestea, metoda precedentă nu poate fi folosită atunci când este nevoie de o reprezentare compactă a arborelui în memorie (de exemplu pentru stocarea într-un fişier), pentru că acei pointeri nu sunt valizi decât în cadrul programului curent.

Din acest motiv, există câteva moduri de a stoca arborii într-o structura liniară de date (vectori), dintre care:

• Înlocuirea pointer-ilor din structurile asociate nodurilor cu întregi ce reprezintă indici într-un vector de astfel de structuri. Primul element din vector va fi rădăcina arborelui, şi va exista un contor curent (la nivelul întregului vector) care indică următoarea poziţie liberă. Atunci când un nod trebuie adăugat în arbore, i se va asocia valoarea curentă a contorului, iar acesta va fi incrementat. În nodul părinte se va reţine indicele în vector al noului nod, în locul adresei lui în memorie (practic acesta este un mic mecanism de alocare de memorie, pe care îl gestionăm noi).
• Eliminarea totală a informaţiei legate de predecesori, şi folosirea unei formule de calcul a părintelui si a descendenţilor unui nod pe baza indicelui acestuia în vector.

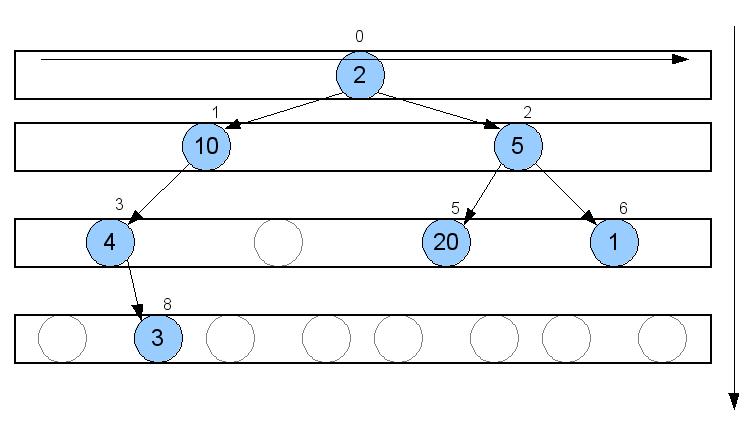
Pentru un arbore binar, cea de-a doua modalitate se implementează conform figurii de mai jos:

Se consideră că arborele este aşezat în vector în ordine (începând de la 0) de la primul nivel până la ultimul, iar nodurile fiecărui nivel se aşează de la stânga la dreapta. Poziţiile fiecărui nod în nivel se consideră ca şi când arborele ar fi complet (iar nodurile lipsă sunt ignorate).

Reprezentarea liniara (sub formă de vector) pentru un arbore binar complet devine:

Se constată că poziţia nodului rădăcină în vector este 0, iar pentru fiecare nod în parte, părintele şi descendenţii se pot calcula după formulele:

• Parinte(i) = (i - 1) / 2, unde i este indicele nodului curent
• IndexStanga(i) = 2 * i + 1, unde i este indicele nodului curent
• IndexDreapta(i) = 2 * i + 2, unde i este indicele nodului curent

În cele ce urmează vom considera un heap ca fiind de fapt un min-heap. Noţiunile sunt perfect similare şi pentru max-heap-uri.

Un min-heap binar este un arbore binar în care fiecare nod are proprietatea că valoarea sa este mai mare sau egală decât cea a părintelui său.

Într-o enunțare echivalentă:

Un min-heap binar este un arbore binar în care fiecare nod are proprietatea că valoarea sa este mai mică sau egală decât cea a tuturor descendenților săi.

H[Parinte(x)] <= H[x]

H[x] reprezintă valoarea nodului x, din vectorul H asociat arborelui.

În mod similar, un max-heap are semnul inegalităţii inversat. Astfel, putem defini şi recursiv proprietatea de heap pentru orice (sub)arbore:

• nodul rădăcină trebuie să respecte proprietatea de heap (inegalitatea);
• cei doi subarbori descendenţi sa fie heap-uri.

Pentru a implementa operaţiile de inserare, ştergere, etc. pentru un heap, vom avea nevoie mai întâi de două operaţii elementare:

• pushDown, care presupune că heap-ul a fost modificat într-un singur nod şi noua valoare este mai mare decât cel puţin unul dintre descendenţi, şi astfel ea trebuie “cernută” către nivelurile de jos, până când heap-ul devine din nou valid.

• pushUp, care presupune că valoarea modificată (sau adăugată la sfârşitul vectorului, în acest caz) este mai mică decât părintele, şi astfel se propagă acea valoare spre rădăcina arborelui, până cand heap-ul devine valid.

Având implementate cele două operaţii de bază, putem defini operaţiile uzuale de manipulare a heap-urilor:

Operația întoarce valoarea minimă din min-heap. Valoarea se va afla la indexul 0 al vectorului de implementare a heap-ului.

Adaugă o nouă valoare la heap, crescându-i astfel dimensiunea cu 1.

Algoritmul pentru această funcție este următorul:

1. introducem elementul de inserat pe prima poziție liberă din vectorul de implementare a heap-ului (în principiu dimVect);
2. “împingem” elementul adăugat în vector până la poziția în care se respectă proprietatea de heap; veți folosi funcția pushUp.

Pseudocod:

push(X)
{
    heap[dimVec] = X;
    dimVec++;
    pushUp(dimVec - 1);
}

Funcția aceasta scoate valoarea minimă din heap (și reactualizează heap-ul). Poate întoarce valoarea scoasă din heap.

Pentru a face operația de pop veți urma pașii:

1. elementul minim din heap (de pe prima poziție) va fi interschimbat cu elementul de pe ultima poziție a vectorului;
2. dimensiunea vectorului va fi redusă cu 1 (pentru a ignora ultimul element, acum cel pe care doream să-l înlăturăm)
3. vom “împinge” nodul care se afla acum în rădăcina heap-ului către poziția în care trebuie sa fie pentru a fi respectată proprietatea de heap; acest lucru se va face cu funcția pushDown.

Pseudocod:

extractMin()
{
    interschimba(heap[0], heap[dimVec - 1]);
    dimVect--;
    pushDown(0);
}

Întrucât operaţiile de extragere a minimului şi de adăugare/reconstituire sunt efectuate foarte eficient (complexităţi de O(1), respectiv O(log n) ), heap-ul poate fi folosit într-o multitudine de aplicaţii care necesită rapiditatea unor astfel de operaţii. O aplicaţie importantă o reprezintă sortarea, care poate fi implementată foarte eficient folosind heap-uri. Complexitatea acesteia este O(n*log n), aceeaşi cu cea de la quick sort şi merge sort. Există mai multe metode de a implementa această sortare, dintre care prezentăm doua dintre ele:

1. Se inserează, pe rând, în heap, toate elementele din vectorul nesortat. Apoi într-un alt şir se extrag minimele. Noul şir va conţine vechiul vector sortat.
2. Se implementează funcţiile din secţiunile precedente pentru un max-heap, şi apoi se foloseşte următorul algoritm (în pseudocod):

HeapSort() 
{
    ConstruiesteMaxHeap();
    for (i=dimHeap-1; i>=1; i--) 
    {
        // Punem maximul la sfarsitul vectorului
        interschimba(heap[0], heap[i]);
        // 'Desprindem' maximul de heap (valoarea ramanand astfel in pozitia finala)
        dimHeap--;
        // Reconstituim heap-ul ramas
        pushDown(0);
    }
}

Porniți exercițiile de la scheletul de cod oferit. Modificați main.cpp, adăugând și testând toate operațiile din clasa Heap.

1. [1p] heap.h Definiţi o structură de vector pe care să poată fi folosite operaţiile de heap-uri, şi funcţii de construcţie şi eliberare a structurii:

• [0.5p] Constructor pentru inițializarea unui heap. capVect reprezintă numărul maxim de elemente din vector. Codul va trebui să aloce memorie separată şi apoi să lucreze cu acea memorie.

template <typename T>
Heap<T>::Heap(int capVect)
{
    // TODO 1.1
}

• [0.5p] Funcție pentru eliberarea memoriei alocate pentru values.

template <typename T>
Heap<T>::~Heap()
{
    // TODO 1.2
}

2. [3p] Implementaţi operaţiile elementare de lucru cu heap-uri, prezentate în secţiunile anterioare:

• [1p] Implementati functiile de calcul ai parintelui si ai descendentilor.

template <typename T>
int Heap<T>::parent(int poz)
{
    // TODO 2.1
}
 
template <typename T>
int Heap<T>::leftSubtree(int poz)
{
    // TODO 2.1
}
 
template <typename T>
int Heap<T>::rightSubtree(int poz)
{
    // TODO 2.1
}

Cele trei funcţii de mai sus vor întoarce -1 în cazul în care părintele, respectiv descendenţii nu există.

• [2p] Implementati pushUp si pushDown.

template <typename T>
void Heap<T>::pushUp(int poz)
{
    // TODO 2.2
 
}
 
template <typename T>
void Heap<T>::pushDown(int poz)
{
    // TODO 2.2
 
}

3. [1p] Implementaţi operaţiile uzuale de lucru cu heap-uri:

template <typename T>
void Heap<T>::insert(T x)
{
    // TODO 3
}
 
template <typename T>
T Heap<T>::peek()
{
    // TODO 3
}
 
template <typename T>
T Heap<T>::extractMin()
{
    // TODO 3
}

4. [2p] p4.cpp Implementaţi algoritmul de sortare folosind heap-uri, alegând una dintre cele două metode prezentate mai sus. Testați implementarea voastră a sortării rulând scriptul de testare test.sh.

Obs.:

• Se va citi întâi numărul n de elemente, iar apoi n numere care trebuie sortate.
• Citirea se face de la stdin. Nu modificați afișarea! Afișarea are formatul folosit pentru script-ul de testing.

BONUS! [1p] Implementaţi şi celelalta metoda de sortare prin heap-uri, în afară de cea aleasă iniţial. Pentru testare se va modifica doar funcția heapSort și se va executa tot scriptul test.sh.

[1] C++ Reference

[2] Thomas H. Cormen, Charles E. Leiserson, Ronald R. Rivest -“Introducere în Algoritmi” (Capitolul 7 - Heapsort)

[3] Heap Data Structure

[4] Binary Heap

[5] Heap Sort