Responsabili:

• Armand Nicolicioiu
• Alexandru-Mihai Stroie
• Cosmin Petrișor

În urma parcurgerii acestui articol studentul va:

• înțelege conceptul unui arbore echilibrat de căutare
• exemplifica acest concept pe structura de treap
• implementa operațiile de adăugare nod, ștergere nod și rotiri
• face operații mai complexe si parcurgri de treapuri
• intelege cum functioneaza structurile AVL si Red-Black Tree

O structură de date este o metodă de a reține anumite date astfel încât operațiile cu acestea (căutare, inserare, ștergere) să fie făcute cât mai eficient și să respecte cerințele programatorului. De multe ori, o anumită structură de date se află la baza unui algoritm sau sistem, iar o performanță bună a acesteia (complexitate spațială și temporală cât mai mică) influențează performanța întregului sistem.

În laboratoarele precedente am observat că un arbore binar de căutare de înălțime h implementează operațiile descrise mai sus într-o complexitate de O(h). Dacă acest arbore binar nu este capabil să gestioneze elementele ce sunt inserate pentru a își menține o structura echilibrată atunci complexitatea pe operațiile de bază va crește.

Treapurile sunt un bun exemplu de arbori de căutare echilibrați, cel mai des folosiți datorită implementării relativ ușoare (comparativ cu alte structuri similare cum ar fi Red-Black Trees, AVL-uri sau B-Trees), dar și a modului de operare destul de intuitiv. Fiecare nod din treap va reţine două câmpuri:

• cheia - informația care se reține în arbore și pe care se fac operațiile de inserare, căutare și ștergere
• prioritatea - un număr pe baza căruia se face echilibrarea arborelui

Această structură trebuie să respecte doua proprietati (sau invarianți):

• Proprietatea de arbore binar de căutare → binary search tree (tr): cheia unui nod va fi mai mare sau egală decât cheia fiului stânga, dacă există şi mai mică sau egală decât cheia fiului dreapta, dacă există. Cu alte cuvinte o parcurgere inordine a arborelui va genera șirul sortat de chei.
• Proprietatea de heap (eap): prioritatea unui nod este mai mare sau egală decât prioritățile fiilor.

Se poate observa că numele structurii de date provine din acești doi invarianți: tr-eap.

Mai jos avem codul pentru structura nodului unui treap; se pot observa asemănările cu structura de arbore binar și cu cea de heap.

Treap.h

template <typename T> struct Treap {
  T key;
  int priority;
  Treap<T> *left, *right;
};

Mai jos este descris pseudocodul pentru operațiile de bază făcute cu treapuri.

Deoarece treapul respecta proprietatea de arbore binar de cautare, căutarea se face exact ca la acesta. Vezi laboratorul 9.

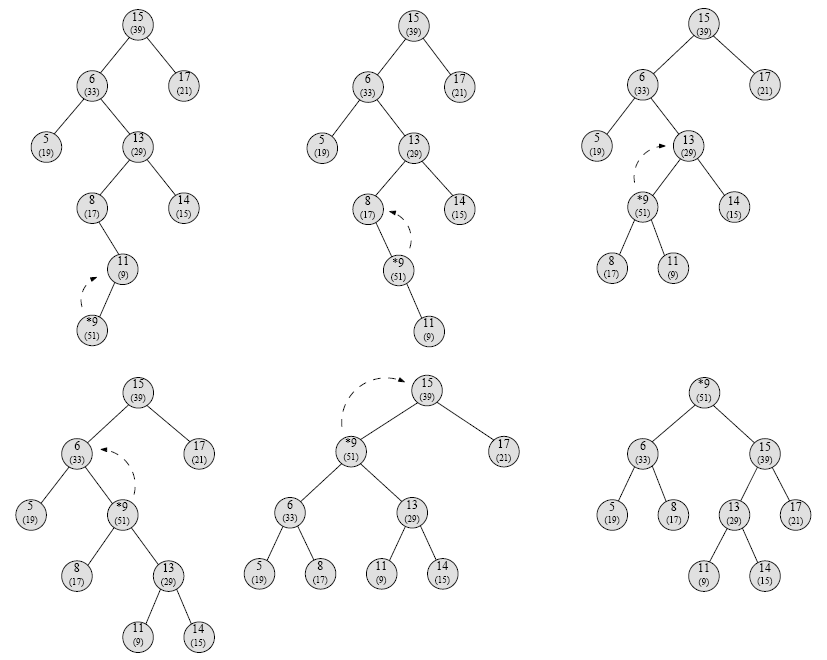
Inserarea unui nod se face generând o prioritate aleatoare pentru acesta și procedând asemănător ca pentru un arbore binar de căutare, adăugând nodul la baza arborelui printr-o procedură recursivă, pornind de la rădăcină.

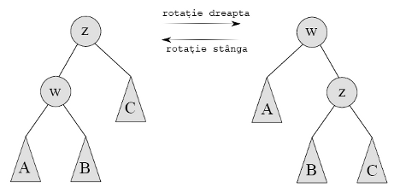
Deși inserarea menține invariantul arborelui de căutare, invariantul de heap poate să nu se mai respecte. De aceea, trebuie definite operații de rotire (stânga sau dreapta), care să fie aplicate unui nod în cazul în care prioritatea sa este mai mare decât ce a părintelui său.

Mai jos avem pseudocodul pentru operația de inserare.

insert(nod, cheie, prioritate) {
    // Daca gasim o frunza, inseram valoarea dorita la acea pozitie
    if nod == NULL
        nod = creeaza nou nod pe baza de cheie si prioritate
        return nod

    if cheie < nod.cheie
        nod.stanga = insert(nod.stanga, cheie, prioritate)
        // Subarborele drept nu a fost modificat, deci verificam schimbarile din stanga
        // Asiguram pastrarea proprietatii de heap
        if nod.stanga.prioritate > nod.prioritate
            rotireDreapta(nod)
            
    else
        nod.dreapta = insert(nod.dreapta, cheie, prioritate)
        // Subarborele stang nu a fost modificat, deci verificam schimbarile din dreapta
        // Asiguram pastrarea proprietatii de heap
        if nod.dreapta.prioritate > nod.prioritate
            rotireStanga(nod)
}

Spre exemplu, dacă am dori să inserăm nodul cu cheia 9 şi prioritatea 51, pașii vor arată în felul următor:

Cele două tipuri de rotiri sunt prezentate vizual în imaginea de mai jos:

Operația de ștergere este inversul operației de inserare și se aseamăna foarte mult cu ștergerea unui nod în cadrul unui heap. Nodul pe care îl dorim a fi șters este rotit până când ajunge la baza arborelui, iar atunci este șters. Pentru a menține invariantul de heap, vom face o rotire stânga dacă fiul drept are o prioritate mai mare decât fiul stâng și o rotire drepta în caz contrar.

sterge(nod, cheie) {
    if nod == NULL
        return
 
    if cheie < nod.cheie
        sterge(nod.stanga, cheie)
        
    else if cheie > nod.cheie
        sterge(nod.dreapta, cheie)
        
    else if nod.stanga == NULL si nod.dreapta == NULL
        sterge nod
        
    else if nod.stanga.prioritate > nod.dreapta.prioritate
        rotireDreapta(nod)
        sterge(nod, cheie)
        
    else
        rotireStanga(nod)
        sterge(nod, cheie)
}

• arbore binar de cautare echilibrat dupa inaltime
• arborele se reechilibreaza(rebalancing) dupa fiecare inserare sau stergere

Diferenta intre 2 subarbori ai oricarui nod este maxim 1. Se defineste:

• factor_de_balans(nod) = inaltime(subarbore_stang(nod)) - inaltime(subarbore_drept(nod))
• invariant = factor_de_balans(nod) este -1, 0 sau 1

La inserare se adauga nodul astfel incat sa aiba proprietatea de arbore binar de cautare, iar dupa se verifica factorul de balansare si se incepe sau nu balansarea lui. Balansarea lui se face cu rotatii duble.

• Rotatie simpla L
• Exemplu de rotatie RL

Cele 4 tipuri de rotatii (LL LR RL RR):

• daca factorul de balans este pozitiv
  • daca factorul de balans al nodului stang este pozitiv
    • LL
  • daca factorul de balans al nodului stang este negativ
    • LR
• daca factorul de balans este negativ
  • daca factorul de balans al nodului drept este pozitiv
    • RL
  • daca factorul de balans al nodului drept este negativ
    • RR

Un arbore rosu-negru este un arbore binar de cautare care are un bit suplimentar pentru memorarea fiecarui nod: culoarea acestuia, care poate fi rosu sau negru. Prin restrângerea modului în care se coloreaza nodurile pe orice drum de la radacina la o frunza, arborii rosu-negru garanteaza ca nici un astfel de drum nu este mai lung decât dublul lungimii oricarui alt drum, deci ca arborele este aproximativ echilibrat.

Un arbore binar de cautare este arbore rosu-negru daca el îndeplineste urmatoarele proprietati rosu-negru:

• Fiecare nod este fie rosu, fie negru.
• Fiecare frunza (nil) este neagra.
• Daca un nod este rosu, atunci ambii fii ai sai sunt negri.
• Fiecare drum simplu de la un nod la un descendent care este frunza contine acelasi numar de noduri negre.

Schelet

1) [4.5p] Implementați următoarele funcții de bază pentru un treap:

• [1p] Căutare
• [2p] Rotiri stânga și dreapta
• [1.5p] Inserare

2) [1.5p] Implementați și funcția de ștergere pentru un treap.

3) [1p] Realizați o parcurgere a treap-ului astfel încât să obțineți cheile sortate crescător/descrescător.

4) [1.5p] Folosiți acest tool pentru a vizualiza cum funcționează un AVL.

5) [1.5p] Folosiți acest tool pentru a vizualiza cum funcționează un Red-Black Tree

Pentru exercițiile 4 și 5 introduceți datele din exemplul oferit în laborator și încercați să preziceți la fiecare pas care va fi următoarea configurație.

Această secțiune nu este punctată și încearcă să vă facă o oarecare idee a tipurilor de întrebări pe care le puteți întâlni la un job interview (internship, part-time, full-time, etc.) din materia prezentată în cadrul laboratorului.

1. Complexitatea pentru operațiile de bază ale Treap-urilor.
2. Implementare unei/unor funcții(rotire stânga/dreapta, inserare, ștergere).
3. Cum se menține structura de arbore echilibrat?
4. Aflarea celei mai mici/mari valori din structură.

1. Fast Set Operations Using Treaps
2. Randomized Binary Search Trees
3. Balanced Search Trees
4. Red-black Tree
5. AVL Tree
6. B-Tree