Laborator 6 - Grafuri - Basics
Responsabili
Obiective
În urma parcurgerii acestui laborator, studentul va fi capabil să:
- înțeleagă operațiile de parcurgere a grafurilor și diferențele dintre ele.
- implementeze parcurgerile pe grafuri având la dispoziție structurile de date studiate.
- evalueze complexitatea parcurgerii grafurilor.
Ce este un graf?
Un graf este o pereche de mulţimi G = (V, E). Mulțimea V conține nodurile grafului (vertices), iar mulțimea E conține muchiile sale (edges), fiecare muchie stabilind o relație de vecinătate între două noduri. Mulţimea E este inclusă în mulţimea VxV.
Diferenţa între graf orientat şi graf neorientat
Dacă pentru orice element al mulţimii E, e = (u, v), elementul e' = (v, u) aparţine de asemenea mulţimii E, atunci spunem că graful este neorientat. În caz contrar, graful este orientat. În cazul grafului orientat, muchiile se mai numesc şi arce.
Reprezentările grafurilor în memorie
În funcţie de problemă şi de tipul grafurilor, avem 2 reprezentări: liste de adiacenţă sau matrice de adiacenţă.
Liste de adiacenţă
Reprezentarea prin liste de adiacenţă constă într-un tablou Adj cu |V| liste, una pentru fiecare vârf din V. Pentru fiecare u din V, lista de adiacenţă Adj[u] conţine referinţe către toate vârfurile v pentru care există muchia (u, v) în E. Cu alte cuvinte, Adj[u] este formată din totalitatea vârfurilor adiacente lui u în G.
Această reprezentare este preferată pentru grafurile rare ( |E| este mult mai mic decât |V|x|V|).
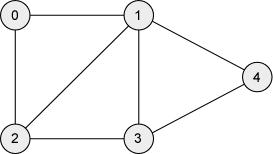
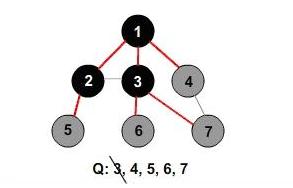
Pentru graful de mai sus, lista de adiacenţă este următoarea:
- 0: 1→2
- 1: 0→2→3→4
- 2: 0→1→3
- 3: 1→2→4
- 4: 1→3
Matrice de adiacenţă
Reprezentarea prin matrice de adiacenţă a unui graf constă într-o matrice A[i][j] de dimensiune |V|x|V| astfel încât:
A[i][j] = 1, dacă muchia(i,j)aparţine luiEA[i][j] = 0, în caz contrar.
Această reprezentare este preferată pentru grafurile dense ( |E| este aproximativ egal cu |V|x|V|).
Pentru graful de mai sus, matricea de adiacenţă este următoarea:
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 2 | 1 | 1 | 0 | 1 | 0 |
| 3 | 0 | 1 | 1 | 1 | 0 |
| 4 | 0 | 1 | 0 | 1 | 0 |
Parcurgerea grafurilor
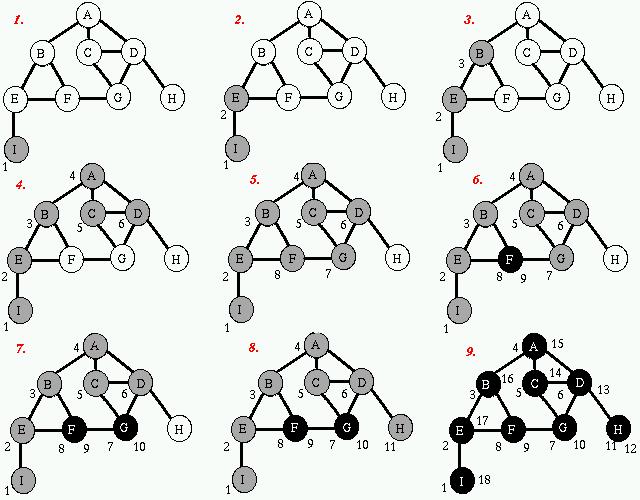
Parcurgerea în lăţime
Parcurgerea în lățime (Breadth-first Search - BFS) presupune vizitarea nodurilor în următoarea ordine:
- nodul sursă (considerat a fi pe nivelul 0)
- vecinii nodului sursă (aceștia constituind nivelul 1)
- vecinii încă nevizitați ai nodurilor de pe nivelul 1 (aceștia constituind nivelul 2)
- vecinii încă nevizitați ai nodurilor de pe nivelul 2
- ş.a.m.d.
Caracteristica esențială a acestui tip de parcurgere este, deci, că se preferă explorarea în lățime, a nodurilor de pe același nivel (aceeași depărtare față de sursă) în detrimentul celei în adâncime, a nodurilor de pe nivelul următor.
Pași de execuție
- colorarea nodurilor. Pe parcurs ce algoritmul avansează, se colorează nodurile în felul următor:
- alb - nodul este nedescoperit încă
- gri - nodul a fost descoperit și este în curs de procesare
- negru - procesarea nodului s-a încheiat
- păstrarea informațiilor despre distanța până la nodul sursă.
- pentru fiecare nod în
d[u]se reține distanța până la nodul sursă (poate fi util în unele probleme)
- obținerea arborelui BFS.
- în urma aplicării algoritmului BFS se obține un arbore de acoperire (prin eliminarea muchiilor pe care nu le folosim la parcurgere). Pentru a putea reconstitui acest arbore, se păstrează pentru fiecare nod dat informația despre părintele său în
p[u].
Pseudocod
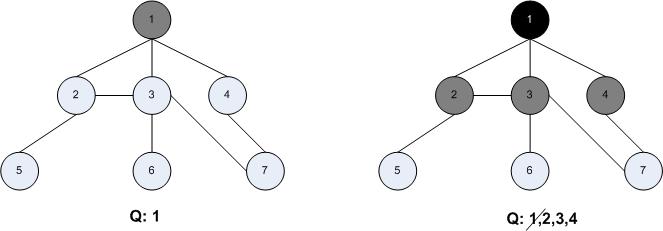
Pentru implementarea BFS se utilizează o coadă (Q) în care inițial se află doar nodul sursă. Se vizitează pe rând vecinii acestui nod şi se pun și ei în coada. În momentul în care nu mai există vecini nevizitați, nodul sursă este scos din coadă.
// Inițializări
pentru fiecare nod u din V
{
culoare[u] = alb
d[u] = infinit
p[u] = null
}
culoare[sursa] = gri
d[sursa] = 0
enqueue(Q,sursa) // Punem nodul sursă în coada Q
// Algoritmul propriu-zis
cât timp coada Q nu este vidă
{
v = dequeue(Q) // Extragem nodul v din coadă
pentru fiecare u dintre vecinii lui v
dacă culoare[u] == alb
{
culoare[u] = gri
p[u] = v
d[u] = d[v] + 1
enqueue(Q,u) // Adăugăm nodul u în coadă
}
culoare[v] = negru // Am terminat de explorat toți vecinii lui v
}
Dacă graful are mai multe componente conexe, algoritmul, în forma dată, va parcurge doar componenta din care face parte nodul sursă. Pe grafuri cu mai multe componente conexe se va aplica în continuare algoritmul pentru fiecare nod rămas nevizitat și astfel se vor obține mai mulți arbori, câte unul pentru fiecare componentă.
Exemplu
Parcurgerea în adâncime
Parcurgerea în adâncime (Depth-First Search - DFS) presupune explorarea nodurilor în următoarea ordine:
- nodul sursă
- primul vecin nevizitat al nodului sursă (îl vom numi
V1) - primul vecin nevizitat al lui
V1(îl vom numiV2) - primul vecin nevizitat al lui
V2 - s.a.m.d.
- în momentul în care am epuizat vecinii unui nod
Vn, continuăm cu următorul vecin nevizitat al nodului anterior,Vn-1
Așadar, spre deosebire de BFS, acest tip de parcurgere pune prioritate pe explorarea în adâncime (la distanțe tot mai mari față de nodul sursă), în detrimentul celei în lățime (pe același nivel).
Pași de execuție
- colorarea nodurilor. Pe parcurs ce algoritmul avansează, se colorează nodurile in felul următor:
- alb - nodul este nedescoperit încă
- gri - nodul a fost descoperit și este în curs de procesare
- negru - procesarea nodului s-a încheiat
- păstrarea informațiilor despre timp. Fiecare nod are două momente de timp asociate:
tDesc[u]- momentul descoperirii nodului (și a schimbării culorii din alb în gri)tFin[u]- momentul în care procesarea nodului s-a încheiat (și culoarea acestuia s-a schimbat din gri în negru)
- obținerea arborelui DFS.
- în urma aplicării algoritmului DFS asupra fiecărei componente conexe a grafului, se obține pentru fiecare dintre acestea câte un arbore de acoperire (prin eliminarea muchiilor pe care nu le folosim la parcurgere). Pentru a putea reconstitui acest arbore, păstram pentru fiecare nod dat informația despre părintele său în
p[u].
Pseudocod
// Inițializări
pentru fiecare nod u din V
{
culoare[u] = alb
p[u] = NULL
tDesc[u] = 0
tFin[u] = 0
}
contor_timp = 0
// Funcţie de vizitare a nodului
vizitare(nod)
{
contor_timp = contor_timp + 1
tDesc[nod] = contor_timp
culoare[nod] = gri
printeaza nod;
}
// Algoritmul propriu-zis
DFS(nod)
{
stiva s;
viziteaza nod;
s.introdu(nod);
cât timp stiva s nu este goală
{
nodTop = nodul din vârful stivei
vecin = află primul vecin nevizitat al lui nodTop.
dacă vecin există
{
p[v] = nodTop
viziteaza v;
s.introdu(v);
}
altfel
{
contor_timp = contor_timp + 1
tFin[nodTop] = contor_timp
culoare[nodTop] = negru
s.scoate(nodTop);
}
}
}
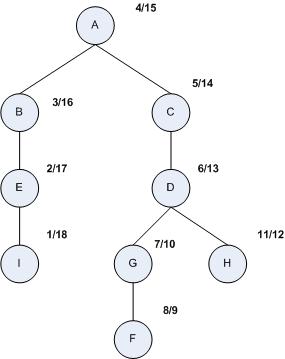
Exemplu
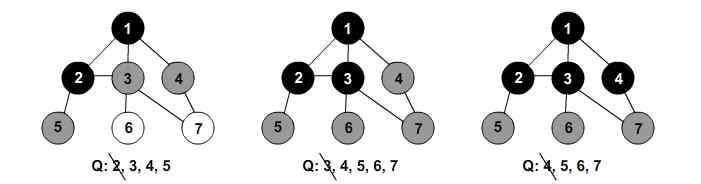
Nodul de pornire este I, iar pentru simplificare vecinii sunt aleși în ordine alfabetică. În stânga nodului este notat tDesc, iar în dreapta tFin. Dacă se afișează nodurile, în urma parcurgerii se obține următorul output: I, E, B, A, C, D, G, F, H
Arborele obținut în urma parcurgerii este următorul:
Complexitate
Pentru ambele tipuri de parcurgeri, complexitatea este O(|E|+|V|) - unde |E| este numărul de muchii, iar |V| este numărul de noduri.
Explicație: în cazul cel mai defavorabil, vor fi explorate toate muchiile și toate nodurile (când graful este liniarizat).
O(|E|+|V|) numai în cazul în care grafurile sunt reținute ca liste de adiacență. În acest caz, lista corespunzătoare nodului x reține numai vecinii nodului x.
În cazul matricei de adiacență, pentru a parcurge vecinii unui nod x, trebuie să parcurgem toate nodurile. Această limitare duce la o complexitate de O(|V|^2)
Schelet
Exerciţii
1) [2p] Implementaţi clasa Graf pentru un graf neorientat, plecând de la antetul definit anterior.
2) [4p] Implementaţi parcurgerea BFS, urmărind paşii descrişi în secţiunea Parcurgerea în lăţime.
3) [4p] Implementaţi parcurgerea DFS, urmărind paşii descrişi în secţiunea Parcurgerea în adâncime.
4) [2p] Implementați parcurgerea DFS, în variantă recursivă.
5) [2p] Implementați, la alegere:
- un algoritm pentru determinarea arborelui parțial de cost minim (ex: Algoritmul lui Kruskal).
- algoritmul Floyd-Warshall.
Interviu
Această secțiune nu este punctată și încearcă să vă facă o oarecare idee a tipurilor de întrebări pe care le puteți întâlni la un job interview (internship, part-time, full-time, etc.) din materia prezentată în cadrul laboratorului.
Cum multe din companiile mari folosesc date stocate sub formă de grafuri (Facebook Open Graph, Google Social Graph şi Page Rank, etc.) la angajare vor dori să vadă ca ştiţi grafuri:
- cum se reprezintă grafurile
- cum funcţionează şi cum se implementează parcurgerile (BFS, DFS)
Puteţi căuta mai multe întrebări pe http://www.careercup.com/ şi pe http://www.glassdoor.com/