Laborator 7 - Grafuri - Advanced
Responsabili
Obiective
În urma parcurgerii acestui laborator, studentul va fi capabil să:
- găsească soluțiile unor probleme folosind algoritmii de parcurgere
- să folosească şi să adapteze algoritmii de parcurgere pentru implementarea soluţiilor găsite
Importanţă
Grafurile sunt utile pentru a modela diverse probleme şi se regăsesc implementaţi în multiple aplicaţii practice:
- reţele de calculatoare (ex: stabilirea unei topologii fără bucle)
- pagini Web (ex: Google PageRank)
- rețele sociale (ex: calcul centralitate)
- hărţi cu drumuri (ex: drum minim)
- modelare grafică (ex: prefuse, graph-cut)
Aplicaţii parcurgeri
Componente conexe
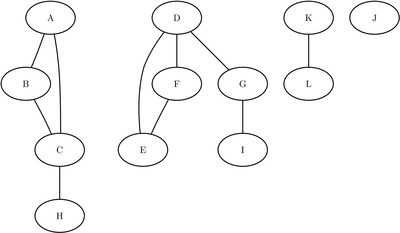
Se numeşte componentă conexă a unui graf neorientat G = (V, E) un subgraf G1 = (V1, E1) în care pentru orice pereche de noduri (A, B) din V1 există un lanţ de la A la B, implicit şi de la B la A.
Observaţie Nu există un alt subgraf al lui G, G2 = (V2, E2) care să îndeplinească această condiţie şi care să îl conţină pe G1. În acest caz, G2 va fi componenta conexă, iar G1 nu.
Algoritm
- Atât o parcurgere
BFS, cât şi unaDFS, pornind dintr-un nod A, va determina componenta conexa din care face parteA. - Pentru a determina toate componentele conexe ale unui graf
G = (V, E), se vor parcurge nodurile dinV. - Din fiecare nod care nu face parte dintr-o componentă conexă găsită anterior, se va porni o parcurgere
BFSsauDFS.
Pseudocod
// Inițializări
pentru fiecare nod u din V
{
stare[u] = nevizitat
}
componente_conexe = 0
// Funcţie de vizitare a nodului
vizitare(nod)
{
stare[nod] = vizitat
printeaza nod
}
// Parcurgerea în adâncime
DFS(nod)
{
stiva s
viziteaza nod
s.introdu(nod)
cât timp stiva s nu este goală
{
nodTop = nodul din vârful stivei
vecin = află primul vecin nevizitat al lui nodTop.
dacă vecin există
{
viziteaza v
s.introdu(v)
}
altfel
{
s.scoate(nodTop)
}
}
}
// Parcurgerea nodurilor din V
pentru fiecare nod u din V
{
dacă stare[u] == nevizitat
{
componente_componente = componente_conexe + 1
DFS(u)
}
}
Exemplu
Aflarea distanţei minime între două noduri
Dacă toate muchiile au același cost, putem afla distanța minimă între două noduri A și B efectuând o parcurgere BFS din nodul A și oprindu-ne atunci când nodul B a fost descoperit. Reamintindu-ne că nivelul unui nod este analog distanței, în muchii, față de sursă, și că BFS descoperă un nod de pe nivelul N numai după ce toate nodurile de pe nivele inferioare au fost descoperite, este ușor de văzut că nivelul nodului B în parcurgere corespunde distanței minime între A și B.
Pentru a reține distanța și drumul exact de la A la B, se vor reține pentru fiecare nod d[x] (distanța de la sursă la x) și p[x] (părintele lui x în drumul de la sursă spre x). În momentul descoperirii unui nod y al cărui părinte este x, se vor face următoarele atribuiri:
d[y] = d[x] + 1 p[y] = x
sursa având d[A] = 0 și p[A] = NULL.
Observații:
- dacă parcurgerea BFS se încheie fără ca nodul B să fi fost descoperit, nu există drum între A și B și deci distanța între acestea este infinită.
- Algoritmul funcționează corect numai în situații de cost uniform (toate muchiile au același cost). Pentru grafuri cu muchii de costuri diferite, sunt necesari algoritmi mai avansați, cum ar fi: Dijkstra, Bellman-Ford sau Floyd-Warshall.
Pseudocod
// Inițializări
pentru fiecare nod u din V
{
stare[u] = nevizitat
d[u] = infinit
p[u] = null
}
// Distanța între sursă și destinație
distanța(sursă, destinație)
{
stare[sursă] = vizitat
d[sursă] = 0
enqueue(Q,sursă) // Punem nodul sursă în coada Q
// BFS
cât timp coada Q nu este vidă
{
v = dequeue(Q) // Extragem nodul v din coadă
pentru fiecare u dintre vecinii lui v
dacă stare[u] == nevizitat
{
stare[u] = vizitat
p[u] = v
d[u] = d[v] + 1
enqueue(Q,u) // Adăugăm nodul u în coadă
}
}
return d[destinație] // Dacă este infinit, nu există drum
}
Sortarea topologică
Se dă un graf orientat aciclic. Orientarea muchiilor corespunde unei relații de ordine de la nodul sursă către cel destinație. O sortare topologică a unui astfel de graf este o ordonare liniară a vârfurilor sale astfel încât, dacă (u,v) este una dintre muchiile grafului, u trebuie să apară înaintea lui v în înșiruire. Dacă graful ar fi ciclic, nu ar putea exista o astfel de înșiruire (nu se poate stabili o ordine între nodurile care alcătuiesc un ciclu).
Sortarea topologică poate fi văzută și ca plasarea nodurilor de-a lungul unei linii orizontale astfel încât toate muchiile să fie direcționate de la stânga la dreapta (să nu existe nici o muchie înapoi, spre părinte).
Pseudocod
// Inițializări
pentru fiecare nod u din V
{
stare[u] = nevizitat
p[u] = NULL
tDesc[u] = 0
tFin[u] = 0
}
contor_timp = 0
// Funcţie de vizitare a nodului
vizitare(nod)
{
contor_timp = contor_timp + 1
tDesc[nod] = contor_timp
stare[nod] = vizitat
printeaza nod
}
// Parcurgere în adâncime
DFS(nod)
{
stiva s
viziteaza nod
s.introdu(nod)
cât timp stiva s nu este goală
{
nodTop = nodul din vârful stivei
vecin = află primul vecin nevizitat al lui nodTop.
dacă vecin există
{
p[v] = nodTop
viziteaza v
s.introdu(v)
}
altfel
{
contor_timp = contor_timp + 1
tFin[nodTop] = contor_timp
s.scoate(nodTop)
}
}
}
// Parcurgere noduri și calculare tDesc și tFin pentru fiecare nod
pentru fiecare nod u din V
{
dacă u nu a fost vizitat
{
DFS(u)
}
}
// Sortare topologica
sortează nodurile din V descrescător în funcție de tFin[nod]
Exemplu
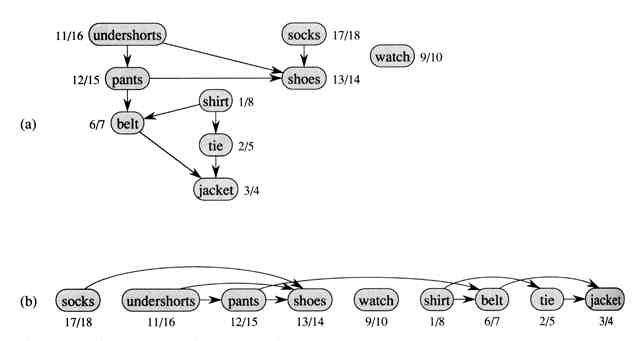
Profesorul Bumstead își sortează topologic hainele înainte de a se îmbrăca.
- fiecare muchie
(u, v) înseamna că obiectul de îmbrăcăminteutrebuie îmbrăcat înaintea obiectului de îmbrăcamintev. Timpii de descoperire(tDesc)și de finalizare(tFin)obținuți în urma parcurgerii DFS sunt notați lângă noduri. - același graf, sortat topologic. Nodurile lui sunt aranjate de la stânga la dreapta în ordinea descrescătoare a
tFin. Observați că toate muchiile sunt orientate de la stânga la dreapta. Acum profesorul Bumstead se poate îmbrăca liniștit.
Așa cum se observă din imagine, sortarea topologică constă în sortarea nodurilor descrescător după timpii de finalizare. Demonstrația acestei afirmații se face simplu, arătând că nodul care se termină mai târziu trebuie să fie efectuat înaintea celorlalte noduri finalizate.
Graf bipartit
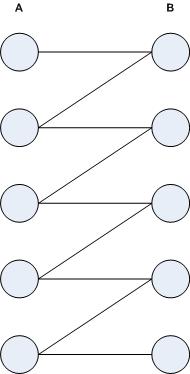
Se numește graf bipartit un graf G = (V, E) în care mulțimea nodurilor poate fi împărțită în două mulțimi disjuncte A și B astfel încât V = A U B şi E este inclus în A x B (orice muchie leagă un nod din A cu un nod din B).
Algoritm
- Pentru a determina dacă un graf este bipartit sau nu, una din metode constă în efectuarea de parcurgeri
BFSși atribuirea de etichete nodurilor conform cu paritatea nivelului acestora în parcurgere (Apentru nodurile de pe nivel par,Bpentru nodurile de pe nivel impar). - Atunci când se adaugă vecinii nevizitați ai unui nod în coadă, se vor verifica de asemenea etichetele vecinilor deja vizitați: dacă se descoperă că unul din aceștia are aceeași etichetă ca cea atribuită nodului curent, graful are o muchie între noduri de pe același nivel și deci nu poate fi bipartit.
- În caz contrar (s-a realizat parcurgerea
BFSfără a apărea această situație), graful este bipartit și nodurile sunt etichetate cu mulțimea din care fac parte.
Pseudocod
sursa = un nod ales aleator din V
nivel[sursa] = par
enqueue(Q, sursa) // Punem nodul sursă în coada Q
// BFS
cât timp coada Q nu este vidă
{
v = dequeue(Q) // Extragem nodul v din coadă
pentru fiecare u dintre vecinii lui v
dacă nivel[u] nedefinit
{
nivel[u] = (nivel[v] == par) ? impar : par
enqueue(Q, u) // Adăugăm nodul u în coadă
}
altfel dacă nivel[u] == nivel[v]
{
// Două noduri consecutive au acelaşi nivel
// Graful nu este bipartit
return false
}
}
// S-a terminat parcurgerea BFS fără să apară două noduri consecutive pe acelaşi nivel
// Graful este bipartit
return true
Exemplu
Ciclu hamiltonian
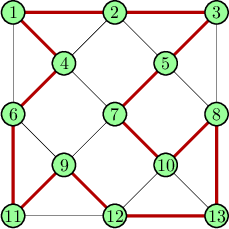
Un lanţ hamiltonian într-un graf orientat sau neorientat G = (V, E), este o cale ce trece prin fiecare nod din V o singură dată. Dacă nodul de început şi cel de sfârşit coincid (este vizitat de două ori) vom spune că lanţul formează un ciclu hamiltonian.
Un graf ce conţine un ciclu hamiltonian se numeşte graf hamiltonian.
Algoritm
În cadrul acestui laborator, vom folosi metoda backtracking pentru găsirea unui ciclu hamiltonian. Pentru contruirea soluţiei, se menţine o listă în care sunt adăugate nodurile parcurse:
- La fiecare pas, vom adăuga unul dintre nodurile care nu se află deja in listă
- Se construieşte recursiv lanţul de lungime_lanţ + 1
- Dacă dimensiunea listei este
n(numărul de noduri din graf), se verifică dacă primul şi ultimul nod din listă sunt adiacente. În caz contrar, s-a găsit un lanţ hamiltonian, dar nu şi un ciclu hamiltonian. - Pentru a afla toate ciclurile hamiltoniene, la revenirea cu succes din apelul recursiv nu se iese din funcţie la găsirea primei potriviri, ci se încearcă în continuare alte posibilităţi.
Pseudocod
// Inițializări
număr_noduri = număr de noduri din V
// Verifica dacă un nod este nou în lanţ
nouÎnLanţ(nod, lanţ)
{
return !lanţ.conţine(nod)
}
// Construieste lanţul hamiltonian
construireLanţ(lanţ, lungime_lanţ)
{
dacă lungime_lanţ == număr_noduri
{
început = lanţ[0]
sfârşit = ultimul element din lanţ
// Există muchie între cele 2 noduri
dacă muchie(început, sfârşit)
{
// Lanţul este ciclu
afişează ciclul
return true
}
}
altfel
{
pentru orice nod u din V
{
sfârşit = ultimul element din lanţ
dacă muchie(u, sfârşit) şi nouÎnLanţ(u, lanţ)
{
addLast(lanţ, u) // Adaugă u la lanţ
construireLanţ(lanţ, lungime_lanţ + 1)
// Pentru afişarea unui singur ciclu hamiltonian linia anterioară este inlocuită cu:
// dacă construireLanţ(lanţ, lungime_lanţ + 1) == true
// return true
removeLast(lanţ, u) // Backtrack
}
}
}
return false
}
// Apelează construirea ciclurilor hamiltoniene
cicluriHamiltoniene
{
// Din moment ce ar trebui să formeze un ciclu, lanţul poate incepe cu orice nod
sursă = alegem un nod aleator din V
addLast(lanţ, sursă)
construireLanţ(lanţ, 1)
}
Exemplu
Schelet
Exerciții
1) [5p]Într-o rețea de socializare pentru gameri există mai multe clanuri. Doi jucători fac parte din același clan dacă există un drum atât de la X la Y, cât și de la Y la X. Când se creează o nouă legatură între doi jucători, clanurile din care ei fac parte se unesc formând un singur clan.
Se dau n numărul de gameri din rețeaua de socializare si m numărul de legături ce există intre aceștia. În continuare, sunt citite cele m legături.
Determinați numărul clanurilor existente în rețea și jucătorii care fac parte din fiecare clan, completând metodele connectedComponents și dfs din Graph.cpp.
Exemplu
- Intrare
12 10 0 1 0 2 1 2 2 3 4 5 4 6 5 6 4 7 7 8 9 10
- Ieșire
4 0 1 2 3 4 5 6 7 8 9 10 11
2) [5p] Un curier, care se află într-un oraș A, trebuie să livreze un pachet într-un oraș B.
Pe hartă se află n orașe, conectate prin m străzi bidirecționale. Se știe faptul că fiecare dintre aceste străzi este parcursă într-un timp constant t.
Se citesc n, m, numărul de teste, cele m străzi și un număr de perechi de orașe A și B egal cu numărul de teste.
Determinați ruta cea mai scurtă pe care poate ajunge curierul în orașul B, în cazul în care aceasta există, completând metoda minPath din Graph.cpp.
Exemplu
- Intrare
7 10 0 1 0 4 1 2 1 3 1 4 2 4 3 5 3 6 4 5 4 6 0 6
- Ieșire
0 4 6
3) [5p] În primii ani de studiu, toți studenții de la Facultatea de Automatică și Calculatoare studiază un număr de N materii obligatorii. Dându-se un set de relații între acestea, cu semnificația că materia din stânga trebuie studiată într-un semestru anterior (nu neapărat din același an), celei din partea dreaptă, găsiti și implementați un algoritm care propune o ordine corectă de studiere a materiilor universitare, care să respecte restricțiile impuse, completând metodele topSort și dfsTopSort din Graph.cpp.
Exemplu
- Intrare
6 4 Programarea_Calculatoarelor Structuri_de_Date Structuri_de_Date Programare_Orientata_pe_Obiecte Matematica1 Fizica Matematica2 Fizica
- Ieșire
Matematica2 Matematica1 Fizica Programarea_Calculatoarelor Structuri_de_Date Programare_Orientata_pe_Obiecte
4) [5p] Dându-se n noduri și m muchii ale unui graf neorientat, determinați dacă acest graf este bipartit și aflați cele două mulțimi care îl formează, completând metoda isBipartite din Graph.cpp.
Exemplu
- Intrare
9 8 0 1 0 6 1 2 2 7 3 6 4 7 4 8 5 8
- Ieșire
0 2 3 4 5 1 6 7 8
5) [2p] Un curier trebuie să livreze pachete în n orașe. Orașele sunt codificate prin numere de la 0 la n-1. Se cunosc m străzi bidirecționale, legături între orașe. Se citesc numarul de teste, apoi pentru fiecare test n, m și cele m străzi bidirecționale.
Sediul curieratului se află în orașul 0. Determinați toate rutele pe care curierul le poate urma astfel încât acesta să efectueze toate livrările și să se întoarcă la sediu, astfel încât el va trece prin fiecare oras o singură data, completând metodele hamiltonianCycles și buildPath din Graph.cpp.
Exemplu
- Intrare
5 7 0 1 1 2 0 3 1 3 1 4 2 4 3 4
- Ieșire
0 1 2 4 3 0