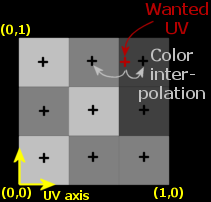
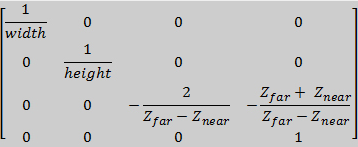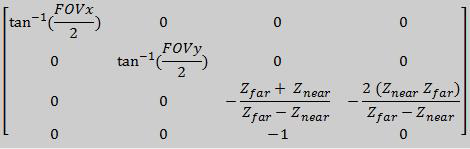Recapitulare EGC
Video Laborator 1:https://youtu.be/Hh-geX8VvxA .
Autor: Anca Morar
Introducere
Grafica pe calculator este un subiect amplu utilizat într-un număr din ce în ce mai mare de domenii. În acest laborator se vor prezenta conceptele ce stau la baza graficii cât și a utilizării procesorului grafic pentru acest scop. Domeniul graficii computerizate necesită cunoștințe variate: matematică, fizică, algoritmică, grafică digitală 2D & 3D, user experience design, etc.
Framework laborator
Întrucât scrierea unei aplicații simple OpenGL nu se poate realiza foarte ușor într-un timp scurt, dar și pentru a putea prezenta mai simplu conceptele de bază ale graficii computerizate moderne, în cadrul laboratoarelor se va lucra pe un framework ce oferă o serie de funcționalități gata implementate. Framework-ul utilizat oferă toate funcționalitățile de bază ale unui motor grafic minimal, precum:
- Fereastra de desenare având la bază un context OpenGL 3.3+ (o să aflați ce înseamnă)
- Suport pentru încărcarea de modele 3D (cunoscute și ca 3D meshes)
- Suport pentru încărcarea de imagini pentru texturarea modelelor 3D
- Suport pentru definirea și încărcarea de shadere OpenGL
De asemenea, pe langă funcționalitățile de bază, framework-ul implementează un model generic pentru scrierea de aplicații OpenGL. Astfel, sunt oferite următoarele aspecte:
- Control pentru fereastra de afișare
- Management pentru input de la tastatură și mouse
- Cameră de vizualizare cu input predefinit pentru a ușura deplasarea și vizualizarea scenei
- Model arhitectural al unei aplicații simple OpenGL, bazat pe toate aspectele prezentate
Funcționalitatea framework-ului este oferită prin intermediul mai multor biblioteci (libraries):
- GLFW
- Site oficial http://www.glfw.org Github https://github.com/glfw/glfw
- Oferă suportul de bază pentru API-ul OpenGL precum context, fereastră, input, etc
- GLEW
- Site oficial http://glew.sourceforge.net Github https://github.com/nigels-com/glew
- Asigură suportul pentru extensiile de OpenGL suportate de procesorul grafic
- GLM
- Site oficial http://glm.g-truc.net Github https://github.com/g-truc/glm
- Funcționalități matematice bazate pe specificațiile limbajului GLSL (shadere OpenGL)
- Asigură interoperabilitate simplă cu API-ul OpenGL
- ASSIMP
- Site oficial http://www.assimp.org Github https://github.com/assimp/assimp
- Open Asset Import Library
- Oferă suport pentru încărcarea de modele și scene 3D
- Suportă majoritatea formatelor de stocare 3D utilizate în industrie
- STB
- Oferă suport pentru încărcare/decodare de imagini JPG, PNG, TGA, BMP, PSD, etc.
- GFX-Components – closed source
- Oferă o serie de funcționalități ce vor fi utilizate începând din primul laborator dar care vor fi implementate și de către studenți pe parcursul laboratoarelor
Structura framework-ului
- /deps
- Bibliotecile utilizate în cadrul framework-ului
- /assets
- Resurse necesare rulării proiecutului
- /textures
- Diverse imagini ce pot fi încărcate și utilizate ca texturi
- /shaders
- Exemple de programe shader - Vertex Shader și Fragment Shader
- /models
- Modele 3D ce pot fi încărcate în cadrul framework-ului
- /fonts
- Fonturi ce pot fi încărcate în cadrul framework-ului la redarea textului
- /src
- Surse C++
- /utils
- O serie de headere predefinite pentru facilitarea accesului la biblioteci
- gl_utils.h
- Adaugă suportul pentru API-ul OpenGL
- glm_utils.h
- Adaugă majoritatea headerelor glm ce vor fi utilizate
- Printare ușoara pentru
glm::vec2, glm::vec3, glm::vec4prin intermediul operatorului C++ supraîncărcat:operator«
- math_utils.h
- Simple definiții preprocesor pentru MIN, MAX, conversie radiani ⇔ grade
- memory_utils.h
- Simple definiții preprocesor pentru lucrul cu memoria și pe biți
- text_utils.h
- Functii utile pentru lucrul cu string-uri
- windows_utils.h
- Simple definiții preprocesor pentru lucrul fereastra GLFW
- /components
- Diverse implementări ce facilitează lucrul în cadrul laboratoarelor
- simple_scene.cpp
- Model de bază al unei scene 3D utilizată ca bază a tuturor laboratoarelor
- camera_input.cpp
- Implementare a unui model simplu de control FPS al camerei de vizualizare oferite de biblioteca GFX-Components
- text_renderer.cpp
- Implementare simpla pentru redarea a unui text 2D sub forma unui HUD
- /core
- API-ul de bază al framwork-ului GFX
- /gpu
- gpu_buffers.cpp
- Asigură suportul pentru definirea de buffere de date și încărcarea de date (modele 3D) pe GPU
- mesh.cpp
- Loader de modele 3D atât din fișier cât și din memorie
- shader.cpp
- Loader de programe Shader pentru procesorul grafic
- texture2D.cpp
- Loader de texturi 2D pe GPU
- /managers
- resource_path.h
- Locații predefinite pentru utilizarea la încărcarea resurselor
- texture_manager.cpp
- Asigură încărcare și management pentru texturile Texture2D
- Încarcă o serie de texturi simple predefinite
- /window
- window_callbacks.cpp
- Asigură implementarea funcțiilor de callback necesare de GLFW pentru un context OpenGL oarecare
- Evenimentele GLFW sunt redirecționare către fereastra definită de Engine
- window_object.cpp
- Oferă implementarea de fereastră de lucru, suport predefinite definire pentru callbacks, dar și un model de buffering pentru evenimente de input tastatură și mouse
- input_controller.cpp
- Prin moștenire oferă suport pentru implementarea callback-urilor de input/tastatură. Odată instanțiat, obiectul se va atașa automat pe fereastra de lucru (pe care o obține de la Engine) și va primi automat evenimentele de input pe care le va executa conform implementării
- În cadrul unui program pot exista oricâte astfel de obiecte. Toate vor fi apelate în ordinea atașării lor, dar și a producerii evenimentelor
- engine.cpp
- Asigură inițializarea contextului OpenGL și a ferestrei de lucru
- world.cpp
- Asigură implementarea modelului de funcționare al unei aplicații OpenGL pe baza API-ului oferit de Framework
- /lab_m1
- Implementările pentru fiecare laborator EGC
- Fiecare laborator va pleca de la baza oferită de SimpleScene
Funcționarea unei aplicații grafice (OpenGL)
Orice aplicație trebuie să asigure funcționalitatea pe o anumită perioadă de timp. În funcție de cerințe această perioadă poate fi :
- deterministă - programul va executa un anumit task iar apoi se va închide (majoritatea programelor create in cadrul facultății până în acest moment respectă acest model)
- continuă - rulează unul sau mai multe task-uri în mod continuu (până in momentul în care utilizatorul sau un eveniment extern închide aplicația).
Aplicațiile grafice cu suport de vizualizare în timp real (de exemplu jocurile, sau de exemplu ce vom face noi la EGC) se regăsesc în cel de-al doilea model și au la bază funcționarea pe baza unei bucle (loop) de procesare.
În cadrul framework-ului EGC acest loop constă într-o serie de pași (vezi World::LoopUpdate()):
- Se interoghează evenimentele ferestrei OpenGL (input, resize, etc.)
- Evenimentele sunt salvate pentru a fi procesate mai tarziu
- Se estimează timpul de execuție pentru iterația actuală (timpul de execuție al iterației precedente)
- Se procesează evenimentele salvate anterior
- Se procesează frame-ul actual (este indicat să se ia în considerare timpul de execuție în cadrul modificărilor pentru a oferi actualizare independentă de timp)
- Opțional: În cazul double sau triple buffering se interschimbă bufferele de imagine
- Se trece la următorul frame (se revine la primul pas)
- nu oferă posibilitatea de a trata combinații de taste (Exemplu: utilizatorul apasa W și A pentru a deplasa caracterul in diagonală)
- nu oferă informații ce țin de starea continuă a unui eveniment
- Exemplu: Un personaj dintr-un joc trebuie să se deplaseze în față atât timp cât utilizatorul ține apasată tasta W.
- Pentru a trata corespunzător o astfel de logică este necesar să menținem starea tastei W iar atunci când se face deplasarea personajului, aceasta să fie direct proporțională cu timpul trecut de la ultimul frame procesat
- Același lucru se aplică și în cazul butoanelor de la mouse
De asemenea, un model bazat pe buffering al evenimentelor de input oferă posibilitatea de a interoga starea input-ului în orice moment al unui frame, deci ofera și o flexibilitate generală mai mare pentru a implementa noi comportamente/logici. Clasa WindowObject asigură suportul pentru buffering, dar și pentru procesarea ulterioară a evenimentelor prin intermediul obiectelor de tipul InputController.
Recomandăm să citiți documentația GLFW despre tratarea evenimentelor de input pentru a înțelege mai bine conceptele prezentate: http://www.glfw.org/docs/latest/input_guide.html
Multi-buffering
În general, aplicațiile grafice folosesc mai multe buffere de imagini separate pentru a evita apariția artefactelor grafice prin modificarea directă a imaginii randate pe ecran. Astfel, imaginea afișată la momentul T a fost procesată la momentul T-1, sau T-2 (în funcție de dimensiunea bufferului).
Informații adiționale despre această tehnică multi-buffering pot fi obțiunute de pe wiki:
Modelul de funcționare al aplicației de laborator
În cadrul unui laborator modelul aplicației grafice prezentat mai sus este implementat de către clasa World.
Pasul 2 este tratat de către instanțele InputController în timp ce pasul 4 este asigurat de funcțiile FrameStart(), Update(float deltaTime), și FrameEnd() moștenite de la clasa World. Clasa World extinde deja InputController pentru a ușura munca în cadrul laboratorului.
Toate laboratoarele EGC vor fi implementate pe baza SimpleScene ce oferă următoarele facilități:
- scena 3D cu randarea unui sistem cartezian de referință în coordonate OpenGL
- plan orizontal XOZ
- evidențierea spațiului pozitiv (OX, OY, OZ)
- camera predefinită pentru explorarea scenei
- shadere predefinite pentru lucrul în primele laboratoare
- management pentru stocarea shaderelor și modelelor nou create, pe baza unui nume unic
Etapele rulării aplicației
- Se definesc proprietățile pentru fereastra de lucru (
main.cpp) - Se inițializează Engine-ul astfel -
Engine::Init()- Se inițializează API-ul OpenGL (
glfwInit()) - Se creează fereastra de lucru cu un context OpenGL 3.3+
- Se atașează evenimentele de fereastră prin intermediul WindowsCallbacks.cpp
- Se inițializează managerul de texturi
- Se creează și inițializează o nouă scenă 3D de lucru având la bază modelul de update prezentat anterior (main.cpp)
- Se pornește rularea scenei încărcate (
LoopUpdate())
Standardul OpenGL
OpenGL este un standard (API) pe care îl putem folosi pentru a crea aplicații grafice real-time. Este aproape identic cu Direct3D, ambele având o influență reciprocă de-a lungul anilor.
- Mai multe informații despre istoricul OpenGL se pot găsi la adresa: https://en.wikipedia.org/wiki/OpenGL
- Explicații complete prinvind API-ul OpenGL cât și utilizarea acestuia se pot găsi pe pagina oficială a standardului: https://www.opengl.org/sdk/docs/man/
Începând cu 2016 a fost lansat și API-ul Vulkan ce oferă access avansat low-level la capababilitățile grafice moderne ale procesoarelor grafice. Standardul Vulkan este orientat dezvoltării aplicațiilor de înaltă performanță iar complexitatea acestuia depășește cu mult aspectele de bază ce vor fi prezentate în cadrul cusului/laboratorului.
Utilizarea API
Pe parcursul laboratoarelor (dar și a cursului) se va trece prin toate etapele importante ce stau la baza redării grafice. Astfel vor fi învățate concepte precum:
- încărcare și randare de obiecte 3D simple
- funcționarea pipeline-ului grafic
- vizualizare, proiecție, control camera
- utilizare shadere (vertex și fragment shader)
- iluminare
- texturare
Cerințe generale de laborator
- Citiți cu foarte mare atenție Framework-ul de laborator întrucât îl veți utiliza pe tot parcursul laboratorului de EGC inclusiv și la temele de casă
- Citiți comentariile din cod – ar trebui să răspundă la majoritatea întrebărilor pe care le aveți
- Citiți documentația de la __input_controller.h__ întrucât veți utiliza constant funcțiile din cadrul acestei clase (prin suprascriere) pentru definirea de interacțiuni și comportament personalizat
- Dacă nu ințelegeți modelul de funcționare al aplicației rugați asistentul să explice încă o dată cum funcționează toată aplicația
C++
Framework-ul este scris în limbajul C++, ce va fi utilizat pe tot parcursul laboratoarelor. Conceptele utilizate în cadrul laboratorului și care trebuie știute sunt:
- concepte de bază de OOP - obiecte, moștenire, metode virtuale, etc
Generare și compilare
- Pentru generarea soluțiilor compilabile pentru platformele suportate, framework-ul folosește CMake
- Platformele suportate în acest moment de framework sunt:
- Windows (stabil)
- Linux (experimental)
- macOS (experimental)
- Pentru generarea soluției pentru platforma dorită, urmați pașii de instalare și generare descriși la GFX Framework
Visual Studio 2019
- În cadrul laboratorului vom utiliza Visual Studio 2019 Community Edition
- Installer-ul de Visual Studio vine cu posibilitatea de a instala modular doar ceea ce este necesar. Pentru acest laborator trebuie instalat doar modulul default Desktop development with C++, care se regăsește în Workloads
- După generarea cu CMake, framework-ul va conține in folderul de /build un proiect pentru Visual Studio: GFXFramework.sln
- Deschideți soluția în Visual Studio
GLM
În grafică, matematica este folosită peste tot, de la simple matrici pentru rotații până la integrale infinit dimensionale pentru algoritmii folosiți în industria filmului, de aceea ne dorim să avem un suport de matematică robust, bine documentat și nu în ultimul rând cât mai apropiat de formatul OpenGL. În loc să scriem noi o bibliotecă de matematică vom folosi biblioteca GLM. GLM ne oferă rotații, translații, vectori de dimensiune 2/3/4, matrici și multe alte funcționalități avansate (de ex. modele de zgomot). Vom folosi doar cele mai simple funcționalități în laboratoarele de la această materie.
glm::mat4 identity = glm::mat4 (1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1); glm::mat4 identity2 = glm::mat4(1); // short form for writing identity matrices glm::vec3 culoare = glm::vec3(1, 0.5, 1); glm::vec2 directie = glm::vec3(-1, 1); glm::vec3 pozitie = glm::vec3(100, 10, -20); pozitie.x = 2; // you can select components like so: .x .y .z .t .r .g. b. a
Laboratorul 1
Framework
Framework-ul de laborator se găsește pe Github
Puteți să descărcați direct arhiva accesând acest link
Informații laborator
În cadrul laboratorului 1 puteți încărca modele 3D în cadrul scenei și cere afișarea scenei utilizând funcția
RenderMesh(Mesh * mesh, glm::vec3 position, glm::vec3 scale)
Culorile pixelilor prin care se reprezintă scena sunt salvate într-un buffer, numit Framebuffer. Contextul definit oferă automat un astfel de buffer și este configurat să ruleze cu double-buffering
API-ul OpenGL utilizat în cadrul laboratorului:
// defineste un spatiu de desenare in spatiul ferestrei de afisare a aplicatiei // x, y reprezinta coordonatele coltului stanga jos // width, height reprezinta dimensiunea spatiului de desenare. void glViewport(GLint x, GLint y, GLsizei width, GLsizei height); // seteaza culoarea cu care va fi colorat tot ecranul la operatia de clear void glClearColor(float r, float g, float b, float a); // implementeaza operatia de clear void glClear(GL_COLOR_BUFFER_BIT);
Bufferul de culoare utilizat (atât în cadrul laboratorului dar și în mod uzual datorită limitărilor impuse de afișarea pe monitoare) este în format RGBA8. Fiecare componentă (red, green, blue, alpha) este memorată pe 8 biți, deci are o valoare in intervalul 0 – 255. Astfel:
- roșu (255, 0, 0) este reprezentată ca (1, 0, 0) pe procesorul grafic
- galben este (1, 1, 0) și tot așa
Control aplicație
Programul rulat oferă posibilitatea vizualizării scenei create prin intermediul unei camere predefinite.
- W, A, S, D, Q, E - deplasare față, stânga, spate, dreapta, jos, sus
- MOUSE RIGHT + MOUSE MOVE - rotație cameră
Video Laborator 2: https://youtu.be/RtXuIQO8l0U.
Autor: Alex Gradinaru
OpenGL – Date
Dacă am încerca să reducem întregul API de OpenGL la mari concepte acestea ar fi:
- date
- stări
- shadere
Shaderele vor fi introduse pe parcursul cursului.
Stările reprezintă un concept mai larg, OpenGL fiind de fapt un mare automat finit cu o mulțime de stări și posibilități de a seta aceste stări. De-a lungul laboratoarelor o parte din aceste stări vor fi folosite pentru a obține efectele dorite.
Datele conțin informațiile ce definesc scena, precum:
- obiecte tridimensionale
- proprietăți de material ale obiectelor (plastic, sticlă, etc)
- pozițiile, orientările și dimensiunile obiectelor în scenă
- orice alte informații necesare ce descriu proprietăți de obiecte sau de scenă
- vârfurile pătratului - 4 vectori tridimensionali ce definesc poziția fiecărui vârf în spațiu
- caracteristicile vârfurilor
- dacă singura caracteristică a unui vârf în afară de poziție ar fi culoarea am avea încă 4 vectori tridimensionali (RGB)
- topologia pătratului, adică modul în care legăm aceste vârfuri
În cadrul laboratorului vom utiliza coordonata Z = 0. Astfel orice punct tridimensional va deveni P(x,y,0)
Topologie
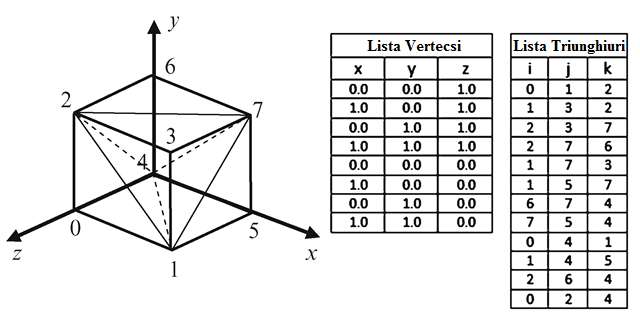
Primitiva de bază în OpenGL este triunghiul. Astfel, așa cum se poate observa și în imaginea de sus, pentru a desena un obiect acesta trebuie specificat prin triunghiuri.
Cubul descris mai sus este specificat prin lista celor 8 coordonate de vârfuri și o listă de 12 triunghiuri care descrie modul în care trebuie unite vârfurile specificate în lista precedentă pentru a forma fețele cubului. Folosind vârfuri și indici putem descrie în mod discret orice obiect tridimensional.
Mai jos regăsiți principalele primitive acceptate de standardul OpenGL 3.3+.
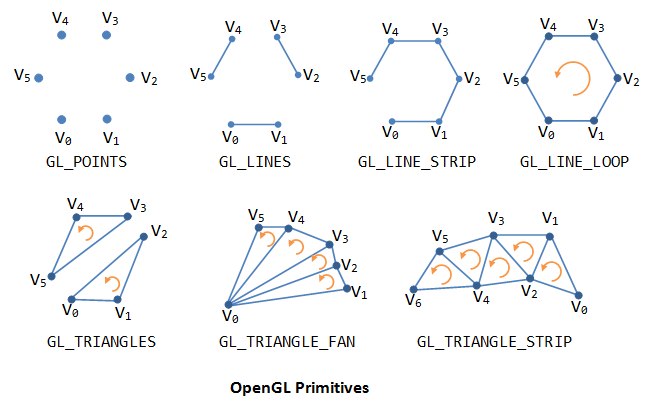
După cum se poate observa, există mai multe metode prin care geometria poate fi specificată:
- GL_LINES și GL_TRIANGLES sunt cele mai des utilizate primitive pentru definirea geometriei
- GL_POINTS este des utilizat pentru a crea sistemele de particule
- Celelalte modele reprezintă doar niște optimizari ale celor 3 primitive de bază, atât din perspectiva memoriei dar și a ușurinței în a specifica anumite topologii însă utilitatea lor este deseori limitată întrucât obiectele mai complexe nu pot fi specificate decât prin utilizarea primitivelor simple
primitive poate fi oricare dintre primitivele menționate în imaginea de mai sus.
Ordinea specificării vârfurilor
O observație importantă legată de topologie este ordinea vârfurilor într-o primitivă solidă (nu linie, nu punct) cu mai mult de 2 vârfuri. Această ordine poate fi în sensul acelor de ceas sau în sens invers.

Face Culling
API-ul OpenGL oferă posibilitatea de a testa orientarea aparentă pe ecran a fiecărui triunghi înainte ca acesta să fie redat și să îl ignore în funcție de starea de discard setată: GL_FRONT sau GL_BACK. Acestă funcționalitate poartă numele de Face Culling și este foarte importantă deoarece reduce costul de procesare total.
Modul cum este considerată o față ca fiind GL_FRONT sau GL_BACK poate fi schimbat folosind comanda glFrontFace (valoarea inițială pentru o față GL_FRONT este considerată ca având ordinea specificării vârfurilor în sens trigonometric / counter clockwise):
// mode can be GL_CW (clockwise) or GL_CCW (counterclockwise) // the initial value is GL_CCW void glFrontFace(GLenum mode);
În mod normal face-culling este dezactivat. Acesta poate fi activat folosind comanda glEnable:
glEnable(GL_CULL_FACE);
Pentru a dezactiva face-culling se folosește comanda glDisable:
glDisable(GL_CULL_FACE);
Pentru a specifica ce orientare a fețelor să fie ignorată se folosește comanda glCullFace
// GL_FRONT, GL_BACK, and GL_FRONT_AND_BACK are accepted. // The initial value is GL_BACK. glCullFace(GL_BACK);
Meshe
Un „mesh” este un obiect tridimensional definit prin vârfuri și indici. În laborator aveți posibilitatea să încărcați meshe în aproape orice format posibil prin intermediul clasei Mesh.
Vertex Buffer Object (VBO)
Un vertex buffer object reprezintă un container în care stocăm date ce țin de conținutul vârfurilor precum:
- poziție
- normală
- culoare
- coordonate de texturare
- etc…
Un vertex buffer object se poate crea prin comanda OpenGL glGenBuffers:
GLuint VBO_ID; // ID-ul (nume sau referinta) buffer-ului ce va fi cerut de la GPU glGenBuffers(1, &VBO_ID); // se genereaza ID-ul (numele) bufferului
În exemplul de mai sus este generat doar 1 singur buffer iar ID-ul este salvat în variabila
VBO_ID.
Pentru a distruge un VBO și astfel să eliberăm memoria de pe GPU se folosește comanda glDeleteBuffers:
glDeleteBuffers(1, &VBO_ID);
Pentru a putea pune date într-un buffer trebuie întâi să legăm acest buffer la un „target”. Pentru un vertex buffer acest „binding point” se numește GL_ARRAY_BUFFER și se poate specifica prin comanda glBindBuffer:
glBindBuffer(GL_ARRAY_BUFFER, VBO_ID);
În acest moment putem să facem upload de date din memoria CPU către GPU prin intermediul comenzii glBufferData:
glBufferData(GL_ARRAY_BUFFER, sizeof(vertices[0]) * vertices.size(), &vertices[0], GL_STATIC_DRAW);
- Comanda citește de la adresa specificată, în exemplul de sus fiind adresa primului vârf
&vertices[0], și copiază în memoria video dimensiunea specificată prin parametrul al 2-lea. - GL_STATIC_DRAW reprezintă un hint pentru driver-ul video în ceea ce privește metoda de utilizare a bufferului. Acest simbol poate avea mai multe valori dar în cadrul laboratorului este de ajuns specificarea prezentată. Mai multe informații găsiți pe pagina de manual a funcției glBufferData
De asemenea, documentația oficială și completă a API-ului OpenGL poate fi gasită pe pagina OpenGL 4 Reference Pages
Index Buffer Object (IBO)
Un index buffer object (numit și element buffer object) reprezintă un container în care stocăm indicii vertecșilor. Cum VBO si IBO sunt buffere, ele sunt extrem de similare în construcție, încărcare de date și ștergere.
glGenBuffers(1, &IBO_ID); glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, IBO_ID); glBufferData(GL_ELEMENT_ARRAY_BUFFER, sizeof(indices[0]) * indices.size(), &indices[0], GL_STATIC_DRAW);
La fel ca la VBO, creăm un IBO și apoi îl legăm la un punct de legatură, doar că de data aceasta punctul de legatură este GL_ELEMENT_ARRAY_BUFFER. Datele sunt trimise către bufferul mapat la acest punct de legatură. În cazul indicilor toți vor fi de dimensiunea unui singur întreg.
Vertex Array Object (VAO)
Într-un vertex array object putem stoca toată informația legată de starea geometriei desenate. Putem folosi un număr mare de buffere pentru a stoca fiecare din diferitele atribute („separate buffers”). Putem stoca mai multe (sau toate) atribute într-un singur buffer („interleaved” buffers). În mod normal înainte de fiecare comandă de desenare trebuie specificate toate comenzile de „binding” pentru buffere sau atribute ce descriu datele ce doresc a fi randate. Pentru a simplifica această operație se folosește un vertex array object care ține minte toate aceste legături.
Un vertex array object este creat folosind comanda glGenVertexArrays:
unsigned int VAO; glGenVertexArrays(1, &VAO);
Este legat cu glBindVertexArray:
glBindVertexArray(VAO);
După ce toate legăturile au fost specificate este recomandat să se dea comanda glBindVertexArray(0) pentru a dezactiva legătura către VAO-ul curent, deoarece altfel riscăm ca alte comenzi OpenGL ulterioare să fie legate la același VAO și astfel să introducem foarte ușor erori în program.
Înainte de comanda de desenare este suficient să legăm doar VAO-ul ca OpenGL să știe toate legatările create la construcția obiectului.
Laborator 2
Descriere laborator
În cadrul laboratorului vom învăța să folosim VAO, VBO, IBO și astfel să generăm și încărcăm geometrie simplă.
Laboratorul pune la dispoziție structura VertexFormat ce va fi utilizată ca bază pentru a crea geometria.
struct VertexFormat { // position of the vertex glm::vec3 position; // vertex normal glm::vec3 normal; // vertex texture coordinate glm::uvec2 text_coord; // vertex color glm::vec3 color; };
Clasa Mesh pune la dispoziție posibilitatea de a încărca geometrie simplă folosind diverse metode:
// Initializes the mesh object using a VAO GPU buffer that contains the specified number of indices bool InitFromBuffer(unsigned int VAO, unsigned int nrIndices); // Initializes the mesh object and upload data to GPU using the provided data buffers bool InitFromData(const std::vector<VertexFormat>& vertices, const std::vector<unsigned int>& indices); // Initializes the mesh object and upload data to GPU using the provided data buffers bool InitFromData(const std::vector<glm::vec3>& positions, const std::vector<glm::vec3>& normals, const std::vector<unsigned int>& indices);
- W, A, S, D, Q, E - deplasare față, stânga, spate, dreapta, jos, sus
- MOUSE RIGHT + MOUSE MOVE - rotație cameră
F3 - afișează/ascunde gridul din scenă
Space - desenează primitivele doar prin puncte sau linii (wireframe) sau geometrie opacă
Video Laborator 3: https://youtu.be/G-rR8QFZVuI
Autor: Stefania Cristea
Transformări 2D
Obiectele 2D sunt definite într-un sistem de coordonate carteziene 2D, de exemplu, XOY, XOZ sau YOZ. În cadrul acestui laborator vom implementa diferite tipuri de transformări ce pot fi aplicate obiectelor definite în planul XOY: translații, rotații și scalări. Acestea sunt definite în format matriceal, în coordonate omgene, așa cum ați învățat deja la curs. Matricile acestor transformări sunt următoarele:
Translația
$$ \begin{bmatrix} {x}'\\ {y}'\\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & t_x\\ 0 & 1 & t_y\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x\\ y\\ 1 \end{bmatrix} $$
Rotația
Rotația față de origine
$$ \begin{bmatrix} {x}'\\ {y}'\\ 1 \end{bmatrix} = \begin{bmatrix} cos(u) & -sin(u) & 0\\ sin(u) & cos(u) & 0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x\\ y\\ 1 \end{bmatrix} $$
Rotația față de un punct oarecare
Rotația relativă la un punct oarecare se rezolvă în cel mai simplu mod prin:
- translatarea atât a punctului asupra căruia se aplică rotația cât și a punctului în jurul căruia se face rotația a.î. cel din urmă să fie originea sistemului de coordonate.
- rotația normală (în jurul originii),
- translatarea rezultatului a.î. punctul în jurul căruia s-a făcut rotația să ajungă în poziția sa inițială
Scalarea
Scalarea față de origine
$$ \begin{bmatrix} {x}'\\ {y}'\\ 1 \end{bmatrix} = \begin{bmatrix} s_x & 0 & 0\\ 0 & s_y & 0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x\\ y\\ 1 \end{bmatrix} $$
Dacă $sx = sy$ atunci avem scalare uniformă, altfel avem scalare neuniformă.
Scalarea față de un punct oarecare
Scalarea relativă la un punct oarecare se rezolvă similar cu rotația relativă la un punct oarecare.
Utilizarea bibliotecii GLM
În cadrul laboratorului folosim biblioteca GLM, care este o bibliotecă implementată cu matrici în formă coloană, exact același format ca OpenGL. Forma coloană diferă de forma linie prin ordinea de stocare a elementelor matricei în memorie, Matricea de translație arată în modul următor în memorie:
glm::mat3 Translate(float tx, float ty) { return glm::mat3( 1, 0, 0, // coloana 1 in memorie 0, 1, 0, // coloana 2 in memorie tx, ty, 1); // coloana 3 in memorie }
Din această cauză, este convenabil ca matricile să fie scrise manual în forma aceasta:
glm::mat3 Translate(float tx, float ty) { return glm::transpose( glm::mat3( 1, 0, tx, 0, 1, ty, 0, 0, 1) ); }
transform2D.h sunt definite funcțiile pentru calculul matricilor de translație, rotație și scalare. În momentul acesta toate funcțiile întorc matricea identitate. În cadrul laboratorului va trebui să modificați codul pentru a calcula matricile respective.
Transformări compuse
De ce sunt necesare matricile? Pentru a reprezenta printr-o singură matrice de transformări o secvență de transformări elementare, în locul aplicării unei secvențe de transformări elementare pe un anume obiect.
Deci, dacă dorim să aplicăm o rotație, o scalare și o translație pe un obiect, nu facem rotația obiectului, scalarea obiectului urmată de translația lui, ci calculăm o matrice care reprezintă transformarea compusă (de rotație, scalare și translație), după care aplicăm această transformare compusă pe obiectul care se dorește a fi transformat.
Astfel, dacă dorim să aplicăm o rotație (cu matricea de rotație $R$), urmată de o scalare ($S$), urmată de o translație ($T$) pe un punct ($x$,$y$), punctul transformat (${x}'$,${y}'$) se va calcula astfel:
$$ \begin{bmatrix} {x}'\\ {y}'\\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & t_x\\ 0 & 1 & t_y\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} sx & 0 & 0\\ 0 & sy & 0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} cos(u) & -sin(u) & 0\\ sin(u) & cos(u) & 0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x\\ y\\ 1 \end{bmatrix} $$
Deci, matricea de transformări compuse $M$ este $M = T * S * R$.
lab3.cpp, există o serie de obiecte (pătrate) pentru care, în funcția Update(), înainte de desenare, se definesc matricile de transformări. Comanda de desenare se dă prin funcția RenderMesh2D().
modelMatrix = glm::mat3(1); modelMatrix *= Transform2D::Translate(150, 250); RenderMesh2D(meshes["square1"], shaders["VertexColor"], modelMatrix);
Pentru exemplul anterior, matricea de translație creată va avea ca efect translatarea pătratului curent cu (150, 250). Pentru efecte de animație continuă, pașii de translație ar trebui să se modifice în timp.
Exemplu:
tx += deltaTimeSeconds * 100; ty += deltaTimeSeconds * 100; model_matrix *= Transform2D::Translate(tx, ty);
deltaTimeSeconds), veți crea animații dependente de platformă.
Exemplu: dacă la fiecare frame creșteți pe tx cu un pas constant (ex: tx += 0.01), atunci animația se va comporta diferit pe un calculator care merge mai repede față de unul care merge mai încet. Pe un calculator care rulează la 50 FPS, obiectul se va deplasa 0.01 * 50 = 0.5 unități în dreapta într-o secundă. În schimb, pe un calculator mai încet, care rulează la 10 FPS, obiectul se va deplasa 0.01 * 10 = 0.1 unități în dreapta într-o secundă, deci animația va fi de 5 ori mai lentă.
Din acest motiv este bine să țineți cont de viteza de rulare a fiecărui calculator (dată prin deltaTimeSeconds, care reprezintă timpul de rulare al frame-ului anterior) și să modificați pașii de translație, unghiurile de rotație și factorii de scalare în funcție de această variabilă.
Transformarea fereastra-poartă
Desenele reprezentate într-un program de aplicație grafică (2D sau 3D) sunt, de regulă, raportate la un sistem de coordonate diferit de cel al suprafeței de afișare.
glViewport().
Exemplu: Dacă viewport-ul meu are colțul din stânga jos (0, 0) și are lățimea 1280 și înălțimea 720, atunci toate obiectele ar trebui desenate în acest interval, dacă vreau să fie vizibile. Acest lucru mă condiționează să îmi gândesc toată scena în (0, 0) - (1280, 720). Dacă vreau să scap de această limitare, pot să îmi gândesc scena într-un spațiu logic (de exemplu îmi creez toate obiectele în spațiul (-1, -1) - (1, 1) și apoi să le desenez în poarta de afișare, dar aplicând ceea ce se numește transformarea fereastră poartă.
În cele ce urmează vedem ce presupune această transformare și cum pot să imi gândesc scena fără să fiu limitat de dimensiunea viewport-ului.
Definiția matematică:
$$ \frac{xp - xpmin}{xpmax - xpmin} = \frac{xf - xfmin}{xfmax - xfmin} $$ $$ \frac{yp - ypmin}{ypmax - ypmin} = \frac{yf - yfmin}{yfmax - yfmin} $$
Transformarea este definită prin 2 dreptunghiuri, în cele două sisteme de coordonate, numite fereastră sau spațiul logic și poartă sau spațiul de afișare. De aici numele de transformarea fereastră-poartă sau transformarea de vizualizare 2D.
F: un punct din fereastră
P: punctul în care se transformă F prin transformarea de vizualizare
Poziția relativă a lui P în poarta de afișare trebuie să fie aceeași cu poziția relativă a lui F în fereastră.
$$ sx = \frac{xpmax - xpmin}{xfmax - xfmin} $$
$$ sy = \frac{ypmax - ypmin}{yfmax - yfmin} $$
- sx, sy depind de dimensiunile celor două ferestre
- tx, ty depind de pozițiile celor două ferestre față de originea sistemului de coordonate în care sunt definite
$$ tx = xpmin - sx * xfmin $$ $$ ty = ypmin - sy * yfmin $$
În final, transformarea fereastră-poartă are următoarele ecuații:
$$ xp = xf * sx + tx $$ $$ yp = yf * sy + ty $$
Considerăm o aceeași orientare a axelor celor două sisteme de coordonate. Dacă acestea au orientări diferite (ca în prima imagine), trebuie aplicată o transformare suplimentară de corecție a coordonatei y.
Efectele transformării
- mărire/micșorare, în funcție de dimensiunile ferestrei și ale porții
- deformare dacă fereastra și poarta nu sunt dreptunghiuri asemenea
- pentru scalare uniformă, $s=min(sx,sy)$, afișarea centrată în poartă presupune o translație suplimentară pe axa Ox sau pe axa Oy:
$$Tsx = (xpmax - xpmin - s*(xfmax - xfmin)) / 2$$ $$Tsy = (ypmax - ypmin - s*(yfmax - yfmin)) / 2$$
- decuparea primitivelor aflate în afara ferestrei vizuale
Matricea transformării fereastră-poartă
De reținut este că transformarea fereastră-poartă presupune o scalare și o translație. Ea are următoarea expresie, cu formulele de calcul pentru sx, sy, tx, ty prezentate anterior:
$$ \begin{bmatrix} xp\\ yp\\ 1 \end{bmatrix} = \begin{bmatrix} sx & 0 & tx\\ 0 & sy & ty\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} xf\\ yf\\ 1 \end{bmatrix} $$
lab3_vis2D:
//2D vizualization matrix glm::mat3 Lab3_Vis2D::VisualizationTransf2D(const LogicSpace & logicSpace, const ViewportSpace & viewSpace) { float sx, sy, tx, ty; sx = viewSpace.width / logicSpace.width; sy = viewSpace.height / logicSpace.height; tx = viewSpace.x - sx * logicSpace.x; ty = viewSpace.y - sy * logicSpace.y; return glm::transpose(glm::mat3( sx, 0.0f, tx, 0.0f, sy, ty, 0.0f, 0.0f, 1.0f)); }
Lab3_Vis2D, este creat un pătrat, în spațiul logic (0,0) - (4,4). De reținut este faptul că acum nu mai trebuie să raportăm coordonatele pătratului la spațiul de vizualizare (cum se intamplă în exercițiile anterioare), ci la spațiul logic pe care l-am definit noi.
logicSpace.x = 0; // logic x logicSpace.y = 0; // logic y logicSpace.width = 4; // logic width logicSpace.height = 4; // logic height glm::vec3 corner = glm::vec3(0.001, 0.001, 0); length = 0.99f; Mesh* square1 = Object2D::CreateSquare("square1", corner, length, glm::vec3(1, 0, 0)); AddMeshToList(square1);
În funcția Update() se desenează același pătrat creat anterior, de 5 ori: patru pătrate în cele patru colțuri și un pătrat în mijlocul spațiului logic. Se definesc 2 viewport-uri, ambele conținând aceleași obiecte. Primul viewport este definit în jumătatea din stânga a ferestrei de afișare, iar al doilea, în jumătatea din dreapta. Pentru primul viewport se definește transformarea fereastră-poartă default și pentru al doilea viewport, cea uniformă. Observați că în al doilea viewport pătratele rămân întotdeauna pătrate, pe când în primul viewport se văd ca dreptunghiuri (adică sunt deformate), dacă spațiul logic și spațiul de vizualizare nu sunt reprezentate prin dreptunghiuri asemenea.
Utilizare
Unde se poate folosi această transformare fereastră-poartă? De exemplu, într-un joc 2D cu mașini de curse, se dorește în dreapta-jos a ecranului vizualizarea mașinii proprii, într-un minimap. Acest lucru se face prin desenarea scenei de două ori.
Dacă de exemplu toată scena (traseul și toate mașinile) este gândită în spațiul logic (-10,-10) - (10,10) (care are dimensiunea 20×20) și spațiul de afișare este (0,0) - (1280, 720), prima dată se desenează toată scena cu parametrii funcției fereastră-poartă anterior menționați:
LogicSpace logic_space = LogicSpace(-10, -10, 20, 20); ViewportSpace view_space = ViewportSpace(0, 0, 1280, 720); vis_matrix *= VisualizationTransf2D(logic_space, view_space);
Dacă la un moment dat mașina proprie este în spațiul (2,2) - (5,5), adică de dimensiune 3×3 și vreau să creez un minimap în colțul din dreapta jos al ecranului de rezoluție 280×220, pot desena din nou aceeași scenă, dar cu urmatoarea transformare fereastră-poartă:
LogicSpace logic_space = LogicSpace(2, 2, 3, 3); ViewportSpace view_space = ViewportSpace(1000, 500, 280, 220); vis_matrix *= VisualizationTransf2D(logic_space, view_space);
Laboratorul 3
Descriere laborator
lab3.cpp, pentru familiarizarea cu transformările 2D de translație, rotație și scalarelab3_vis2D.cpp, pentru familiarizarea cu transformarea fereastră-poartă
Din fisierul main.cpp puteți să alegeți ce laborator rulați:
World *world = new Lab3();
sau
World *world = new Lab3_Vis2D();
Transformarea fereastră-poartă este și ea simulată pentru acest framework, dar veți învăța pe parcurs că ea este de fapt inclusă în lanțul de transformări OpenGL și că nu trebuie definită explicit.
Video Laborator 4: https://youtu.be/huCrfe9sbMQ
Autor: Alex Dinu
Operații de calcul cu vectori
Până acum în laboratoare ați folosit tipul de date glm::vec3 pentru a reprezenta vectori de 3 dimensiuni, în mod special pentru a reprezenta poziția unui obiect în spațiu. Poate apărea însă o confuzie între termenul de vector și poziție: pentru că prin definiție, un vector are o direcție și o magnitudine (sau lungime).
Niște exemple de vectori în spațiul 2D (în 3D este același principiu, dar este mai ușor de observat în 2D) arată așa:

Prin urmare, dacă vrem să vizualizăm vectorii ca o poziție, putem să ne imaginăm un vector cu originea în (0, 0, 0) și apoi cu direcția către locul unde vrem să fie poziția, construind astfel un “vector de poziție” (cum este in acest exemplu, vectorul V).
Principalele operații cu vectori
1. Operatii cu un scalar:

Unde în loc de + pot fi folosiți operatorul de diferență, înmulțire sau împărțire.
2. Opusul unui vector:

Calculul unui vector cu direcția inversă se poate face înmulțind vectorul cu scalarul -1.
3. Adunarea și scăderea vectorilor:
Matematic, adunarea a doi vectori se face făcând suma pe componente, ca în exemplul de mai jos:

Vizual însă, efectul adunării este următorul (regula triunghiului):

În mod asemănător, efectul vizual al scăderii este următorul:

4. Lungimea unui vector:
In mod normal, lungimea se calculeaza folosind teorema lui Pitagora, deci unde lungimea vectorului ar fi: $$length = sqrt(x*x + y*y);$$

În OpenGL, există o funcție în GLM pentru calculul lungimii:
glm::vec3 v = glm::vec3(2, 3, 5); float length = glm::length(v); // 6.164414
glm::vec3 v = glm::vec3(2, 3, 5); glm::vec3 v_norm = glm::normalize(v); // (0.324443, 0.486664, 0.811107)
Normalizarea ajută la lucrul cu vectori, mai ales în cazuri unde ne interesează doar direcția acestora.
5. Produsul scalar (Dot-product):

O aplicație foarte interesantă este atunci când vectorii sunt unitate (au lungime 1), deoarece produsul scalar o să fie valoarea cosinusului. Un exemplu vizual este următorul:
În OpenGL, există o funcție în GLM pentru calculul produsului scalar:
glm::vec3 a = glm::vec3(0, 1, 0); glm::vec3 b = glm::vec3(1, 0, 0); float dotProd = glm::dot(a, b);
6. Produsul vectorial (Cross-product):
Produsul vectorial este definit numit în spațiul 3D, unde primește 2 vectori (care nu sunt paraleli) ca input și produce un al treilea vector care este perpendicular pe cei 2 vectori:

În OpenGL, există o funcție în GLM pentru calculul produsului vectorial:
glm::vec3 a = glm::vec3(0, 1, 0); glm::vec3 b = glm::vec3(1, 0, 0); glm::vec3 crossProd = glm::cross(a, b); // (0, 0, -1)
Transformări 3D
Obiectele 3D sunt definite într-un sistem de coordonate 3D, de exemplu XYZ. În cadrul acestui laborator vom implementa diferite tipuri de transformări ce pot fi aplicate obiectelor: translații, rotații și scalări. Acestea sunt definite în format matriceal, în coordonate omgene, așa cum ați învățat deja la curs. Matricile acestor transformări sunt următoarele:
Translația
$$ \begin{bmatrix} {x}'\\ {y}'\\ {z}'\\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & t_x\\ 0 & 1 & 0 & t_y\\ 0 & 0 & 1 & t_z\\ 0 & 0 & 0 &1 \end{bmatrix} \begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix} $$
Rotația
Rotația față de axa OX
$$ \begin{bmatrix} {x}'\\ {y}'\\ {z}'\\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & cos(u) & -sin(u) & 0 \\ 0 & sin(u) & cos(u) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix} $$
Rotația față de axa OY
$$ \begin{bmatrix} {x}'\\ {y}'\\ {z}'\\ 1 \end{bmatrix} = \begin{bmatrix} cos(u) & 0 & sin(u) & 0\\ 0 & 1 & 0 & 0 \\ -sin(u) & 0 & cos(u) & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix} $$
Rotația față de axa OZ
$$ \begin{bmatrix} {x}'\\ {y}'\\ {z}'\\ 1 \end{bmatrix} = \begin{bmatrix} cos(u) & -sin(u) & 0 & 0\\ sin(u) & cos(u) & 0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix} $$
Rotația față de o axă paralelă cu axa OX
Rotația relativă la o axă paralelă cu axa OX se rezolvă în cel mai simplu mod prin:
- translatarea atât a punctului asupra căruia se aplică rotația cât și a punctului în jurul căruia se face rotația a.î. cel din urmă să se afle pe axa OX
- rotația normală (în jurul axei OX)
- translatarea rezultatului a.î. punctul în jurul căruia s-a făcut rotația să ajungă în poziția sa inițială
Similar se procedeaza și pentru axele paralele cu OY și OZ.
La curs veți învăța cum puteți realiza rotații față de axe oarecare (care nu sunt paralele cu OX, OY sau OZ).
Scalarea
Scalarea față de origine
$$ \begin{bmatrix} {x}'\\ {y}'\\ {z}'\\ 1 \end{bmatrix} = \begin{bmatrix} s_x & 0 & 0 &0 \\ 0 & s_y & 0 &0 \\ 0 & 0 & s_z &0 \\ 0 & 0 & 0 &1 \end{bmatrix} \begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix} $$
Dacă $sx = sy = sz$ atunci avem scalare uniformă, altfel avem scalare neuniformă.
Scalarea față de un punct oarecare
Scalarea relativă la un punct oarecare se rezolvă în cel mai simplu mod prin:
- translatarea atât a punctului asupra căruia se aplică scalarea cât și a punctului față de care se face scalarea a.î. cel din urmă să fie originea sistemului de coordonate
- scalarea normală (față de origine)
- translatarea rezultatului a.î. punctul față de care s-a făcut scalarea să ajungă în poziția sa inițială
Utilizarea bibliotecii GLM
În cadrul laboratorului folosim biblioteca GLM care este o bibliotecă implementată cu matrici în formă coloană, exact același format ca OpenGL. Forma coloană diferă de forma linie prin ordinea de stocare a elementelor matricei în memorie, Matricea de translație arată în modul următor în memorie:
glm::mat4 Translate(float tx, float ty, float tz) { return glm::mat4( 1, 0, 0, 0, // coloana 1 in memorie 0, 1, 0, 0, // coloana 2 in memorie 0, 0, 1, 0, // coloana 3 in memorie tx, ty, tz, 1); // coloana 4 in memorie }
Din această cauză, este convenabil ca matricile să fie scrise manual în forma aceasta:
glm::mat4 Translate(float tx, float ty, float tz) { return glm::transpose( glm::mat4( 1, 0, 0, tx, 0, 1, 0, ty, 0, 0, 1, tz, 0, 0, 0, 1) ); }
transform3D.h sunt definite funcțiile pentru calculul matricilor de translație, rotație și scalare. În momentul acesta toate funcțiile întorc matricea identitate. În cadrul laboratorului va trebui să modificați codul pentru a calcula matricile respective.
lab4.cpp, există o serie de obiecte (cuburi) pentru care, în funcția Update(), inainte de desenare, se definesc matricile de transformări. Comanda de desenare se dă prin funcția RenderMesh(), care are ca parametru și matricea de transformări.
modelMatrix = glm::mat4(1); modelMatrix *= Transform2D::Translate(1, 2, 1); RenderMesh(meshes["box"], modelMatrix);
Pentru exemplul anterior, matricea de translație creată va avea ca efect translatarea cubului curent cu (1, 2, 1). Pentru efecte de animație continuă, pașii de translație ar trebui să se modifice în timp.
Transformarea fereastră-poartă
în laboratorul 3, s-a discutat despre transformarea fereastră-poartă si a fost parcursă matematica din spatele ei. în realitate, transformarea fereastră-poartă face parte din transformările fixe din banda grafică și nu este o operație care poate fi modificată de programatorul care se folosește de OpenGL.
Modul în care se poate interacționa cu transformarea fereastră-poartă în OpenGL este funcția:
glViewport(GLint x, GLint y, GLint width, GLint height)
Această funcție specifică OpenGLului că ceea ce urmează să fie trimis către randare va trebui să apară pe ecran în coordonatele fizice: $$(x, y) – (x + width, y + height)$$
Depth Buffer: Depth bufferul (sau Z bufferul) este o structură în care se menține adâncimea în scenă a fiecărui fragment din imaginea desenată.
glViewport poate fi extrem de util în diverse situații în care s-ar dori redarea mai multor puncte de vedere dintr-o scenă în același timp, ca de exemplu: oglinzi retrovizoare într-un joc cu mașini sau o hartă văzută de sus care se actualizează odată cu mișcarea jucătorului, cum se poate observa în animația de mai jos:

Video Laborator 5: https://youtu.be/HOv-P8QnEAA
Autor: Florin Iancu
Spațiul Obiect
Spațiul obiect mai este denumit și SPAȚIUL COORDONATELOR LOCALE.
Pentru a putea lucra mai eficient și a reutiliza obiectele 3D definite, în general, fiecare obiect este definit într-un sistem de coordonate propriu. Obiectele simple sau procedurale pot fi definite direct din cod însă majoritatea obiectelor utilizate în aplicațiile 3D sunt specificate în cadrul unui program de modelare precum 3D Studio Max, Maya, Blender etc. Definind independent fiecare obiect 3D, putem să îi aplicăm o serie de transformări de rotație, scalare și translație pentru a reda obiectul în scena 3D. Un obiect încărcat poate fi afișat de mai multe ori prin utilizarea unor matrici de modelare, câte una pentru fiecare instanță a obiectului inițial, ce mențin transformările 3D aplicate acestor instanțe.
În general, fiecare obiect 3D este definit cu centrul (sau centrul bazei ca în poza de mai jos) în originea propriului său sistem de coordonate, deoarece în acest fel pot fi aplicate mai ușor transformările de modelare. Astfel, rotația și scalarea față de centrul propriu sunt efectuate întotdeauna față de origine.
Spațiul Lume
Spațiul lume sau SPAȚIUL COORDONATELOR GLOBALE este reprezentat prin intermediul matricei de modelare, aceeași despre care s-a vorbit mai sus. Matricea se obține printr-o serie de rotații, scalări și translații. Prin înmulțirea fiecărui vertex al unui obiect (mesh 3D) cu această matrice, obiectul va fi mutat din spațiul local în spațiul lume, adică se face trecerea de la coordonate locale la coordonate globale.
Folosind matrici de modelare diferite putem amplasa un obiect în scenă de mai multe ori, în locații diferite, cu rotație și scalare diferită dacă este necesar. Un exemplu este prezentat în scena de mai jos.
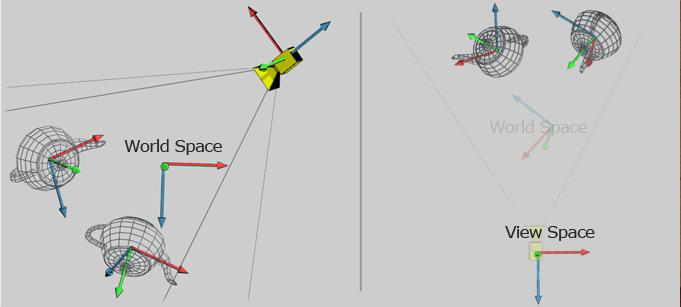
Spațiul de Vizualizare
Spațiul de vizualizare sau SPAȚIUL CAMEREI este reprezentat de matricea de vizualizare.
Matricea de modelare poziționează obiectele în scenă, în spațiul lume. Dar o scenă poate fi vizualizată din mai multe puncte de vedere. Pentru aceasta există transformarea de vizualizare. Dacă într-o scenă avem mai multe obiecte, fiecare obiect are o matrice de modelare diferită (care l-a mutat din spațiul obiect în spațiul lume), însă toate obiectele au aceeași matrice de vizualizare. Transformarea de vizualizare este definită pentru întreaga scenă.
În spațiul lume camera poate să fie considerată ca un obiect având cele 3 axe locale OX, OY, OZ (vezi poza). Matricea de vizualizare se poate calcula folosind funcția glm::lookAt.
glm::mat4 View = glm::lookAt(glm::vec3 posCameraLume, glm::vec3 directieVizualizare, glm::vec3 cameraUP);

Ox,Oy,Oz sunt axele sistemului de coordonate ale lumii (spațiul scenei 3D). Punctul O nu este marcat în imagine. O’x’,O’y’,O’z’ sunt axele sistemului de coordonate al observatorului (spațiul de vizualizare). Punctul O’ nu este marcat în imagine (este înăuntrul aparatului).
Vectorul forward este direcția în care observatorul privește, și este de asemenea normala la planul de vizualizare (planul fiind baza volumului de vizualizare, ce seamănă cu o piramidă și este marcat cu contur portocaliu). Vectorul right este direcția dreapta din punctul de vedere al observatorului. Vectorul up este direcția sus din punctul de vedere al observatorului.
În imagine, observatorul este un pic înclinat, în mod intenționat, în jos, față de propriul sistem de axe. Când observatorul este perfect aliniat cu axele, right coincide cu +x’, up coincide cu +y’, iar forward coincide cu -z’. În imagine, se poate vedea că up nu coincide cu +y’, iar forward nu coincide cu -z’.
Vectorul “up” se proiectează în planul de vizualizare, cu direcția de proiecție paralelă cu normala la planul de vizualizare. Proiecția acestuia dă direcția axei verticale a planului de vizualizare.
În spațiul lume camera poate fi considerată un simplu obiect 3D asupra căruia aplicăm transformările de rotație și translație. Dacă în spațiul lume, camera poate fi poziționată oriunde și poate avea orice orientare, în spațiul de vizualizare (spațiul observator) camera este întotdeauna poziționată în (0,0,0) și privește în direcția OZ negativă.
Matricea de vizualizare conține transformări de rotație și translație, la fel ca și matricea de modelare. De aceea, dacă ținem scena pe loc și mutăm camera, sau dacă ținem camera pe loc și rotim/translatăm scena, obținem același efect:
- Futurama
Totuși, cele două matrici au scopuri diferite. Una este folosită pentru poziționarea obiectelor în scenă, iar cealaltă pentru vizualizarea întregii scene din punctul de vedere al camerei.
glm::lookAt(glm::vec3(3, 5, 7), glm::vec3(1, 0, 0), glm::vec3(0, 1, 0));
Spațiul de Proiecție
După aplicarea transformării de vizualizare, în spațiul de vizualizare, camera se află în origine și privește înspre –OZ. Pentru a putea vizualiza pe ecran această informație este necesar să se facă proiecția spațiului vizualizat de cameră într-un spațiu 2D. Cum spațiul vizibil al camerei poate fi de diferite feluri, cel mai adesea trunchi de piramida (proiecție perspectivă) sau paralelipiped (proiecție ortografică), în OpenGL este necesară trecerea într-un spațiu final numit spațiu de proiecție ce reprezintă un cub centrat în origine cu dimensiunea 2, deci coordonatele X, Y, Z între -1 și +1.
Din spațiul de proiecție este foarte ușor matematic să obținem proiecția finală 2D pe viewport fiind nevoie doar să mapăm informația din cubul [-1,1] scalată corespunzător pe viewport-ul definit de aplicație.
Matricea de Proiecție
Trecerea din spațiul de vizualizare în spațiul de proiecție se face tot utilizând o matrice, denumită matrice de proiecție, calculată în funcție de tipul de proiecție definit. Biblioteca GLM oferă funcții de calcul pentru cele mai utilizate 2 metode de proiecție în aplicațiile 3D, anume: proiecția perspectivă și ortografică
Datele (vertecșii din spațiul de vizualizare) sunt înmulțite cu matricea de proiecție pentru a se obține pozițiile corespunzătoare din spațiul de proiecție.
Proiecția Ortografică
În proiecția ortografică observatorul este plasat la infinit. Distanța până la geometrie nu influențează proiecția și deci nu se poate determina vizibil din proiecție. Proiecția ortografică păstrează paralelismul liniilor din scenă.
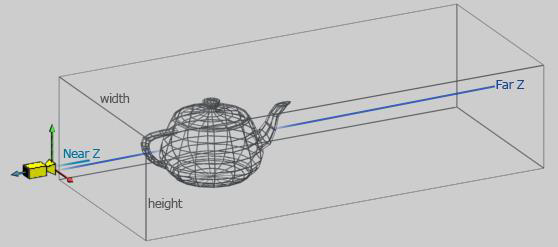
Proiecția ortografică este definită de lățimea și înălțimea ferestrei de vizualizare cât și a distanței de vizualizare dintre planul din apropiere și planul din depărtare. În afara acestui volum obiectele nu vor mai fi văzute pe ecran.
Matricea de proiecție poate fi calculată utilizând funcția glm::ortho unde punctele left, right, bottom, top sunt relative față de centrul ferestrei (0, 0) și definesc înălțimea și lățimea ferestrei de proiecție
glm::mat4 Projection = glm::ortho(float left, float right, float bottom, float top, float zNear, float zFar);
Proiecția Perspectivă
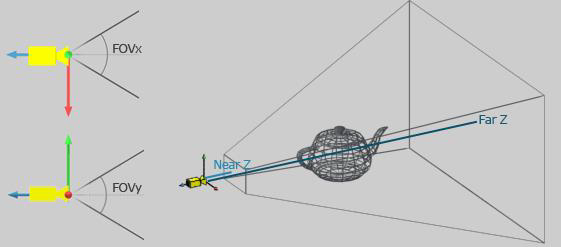
Proiecția perspectivă este reprezentată de un trunchi de piramidă (frustum) definit prin cele 2 planuri, cel din apropiere și cel din depărtare, cât și de deschiderea unghiurilor de vizualizare pe cele 2 axe, OX și OY. În proiecția perspectivă distanța până la un punct din volumul de vizualizare influențează proiecția.
Matricea de proiecție în acest caz poate fi calculată cu ajutorul funcției glm::perspective ce primește ca parametri deschiderea unghiului de vizualizare pe orizontală (Field of View - FoV), raportul dintre lățimea și înălțimea ferestrei de vizualizare (aspect ratio), cât și distanța până la cele 2 planuri zFar și zNear.
glm::mat4 Projection = glm::perspective(float fov, float aspect, float zNear, float zFar);
În cazul proiecției perspectivă, după înmuțirea coordonatelor din spațiul view, componenta w a fiecărui vertex este diferită, ceea ce înseamnă că spațiul de proiecție nu e același pentru fiecare vertex. Pentru a aduce toți vectorii în același spațiu se împarte fiecare componentă a vectorului rezultat cu componenta w. Această operație este realizată automat de procesorul grafic, în cadrul unei aplicații fiind nevoie doar de înmulțirea cu matricea de proiecție.
Volum de vizualizare perspectivă (stânga) și rezultatul obținut (dreapta) în urma aplicării transformării de proiecție asupra geometriei din scenă
Spațiul Coordonatelor de Dispozitiv Normalizate (NDC)
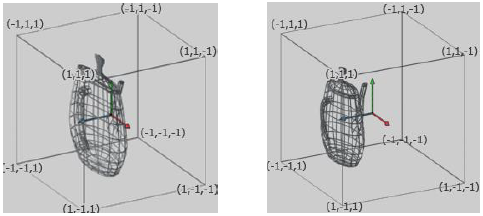
După aplicarea transformărilor de Modelare, Vizualizare și Proiecție iar apoi divizarea cu W a vectorilor, se obține spațiul de coordonate normalizate (NDC) reprezentat de un CUB centrat în origine (0, 0, 0) cu latura 2. Informația din acest cub se poate proiecta foarte ușor pe orice suprafață 2D de desenare definită de utilizator.
Exemplu rezultat al proiecției în coordonate dispozitiv normalizate (NDC). Proiecție ortografică (stânga), perspectivă (dreapta)
Exemplu vizualizare spațiu NDC din direcția camerei (stânga) și proiecția corespunzătoare pentru un anumit viewport (dreapta)
Aplicarea Transformărilor de Modelare, Vizualizare și Proiecție
Aplicarea trasformărilor de Modelare, Vizualizare și Proiecție se face prin înmulțirea fiecărui vertex al geometriei din scenă cu cele 3 matrici calculate.
pos_vertex = Projection * View * Model * pos_vertex
RenderMesh. Înmulțirile respective sunt executate pe procesorul grafic în cadrul programului vertex shader ce va fi introdus începând cu laboratorul următor.
Transformări de Cameră
Implementarea unei camere în cadrul unei aplicații 3D depinde de cerințele aplicației. În practică cele mai utilizate tipuri de implementări de cameră sunt: First person și Third person.
First-person Camera
Camera de tipul First-person presupune faptul că scena 3D este vizualizată din perspectiva ochilor unui observator, adesea uman. Constrângerile de implementare sunt următoarele:
Translația camerei First-person
- translațiile față/spate se calculează utilizând vectorul forward (direcția de vizualizare sau proiecția acestuia în planul orizontal XOZ)
- translațiile sus/jos se calculează utilizând vectorul local Up sau cel mai adesea direcția OY globală (
glm::vec3(0, 1, 0)) - translațiile dreapta/stânga se calculează folosind vectorul local right (ce se poate obține și prin operația de cross product între vectorii forward și up) sau folosind proiecția acestuia pe planul orizontal XOZ
posCamera = posCamera + glm::normalize(direction) * distance;
Rotația camerei First-person
- rotațiile se fac păstrând observatorul pe loc și modificând direcția în care privește acesta
- pentru rotația stânga/dreapta, vectorii forward respectiv right se pot calcula prin aplicarea transformării de rotație în jului axei OY globale. Se poate roti și în jurul axei OY locale (vectorul up), însă în general nu prea are aplicabilitate practică
- vectorul up se poate recalcula folosind cross product între right și forward
forward = RotateWorldOY(angle) * forward; right = RotateWorldOY(angle) * right; up = glm::cross(right, forward);
- rotația sus/jos se poate face rotind vectorii forward respectiv up în jurul vectorului axei OX adică vectorul right (right rămâne constant)
forward = RotateLocalOX(angle) * forward; up = glm::cross(right, forward);
glm::rotate
glm::mat4 = glm::rotate(glm::mat4 model, float angle, glm::vec3 rotationAxis);
- primul parametru reprezintă o matrice de modelare asupra căreia aplicăm transformarea specificată. Atunci când nu avem o transformare precedentă se pornește de la matricea identitate
glm::mat4(1.0f)
- rotationAxis este axa față de care rotim. În cazul nostru pentru rotația față de OX este vectorul right, pentru rotația față de OZ este vectorul forward, sau
glm::vec3(0, 1, 0)pentru rotația față de OY global
- întrucât vectorii utilizați sunt
glm::vec3când facem înmulțirea va trebui să construim un vector de 4 componente ca să putem înmulți cu matricea de 4×4. Puteți construi vectorul astfel:
glm::vec3 forward = ... glm::vec4 newVec = glm::vec4(forward, 1.0);
- Dacă vrem să rotim vectorul “forward” în jurul axei OY globale atunci facem astfel:
// get the rotate vec4 vector glm::vec4 newVector = glm::rotate(glm::mat4(1.0f), angle, glm::vec3(0, 1, 0)) * glm::vec4(forward, 1); // extract the vec3 vector and then normalize it forward = glm::normalize(glm::vec3(newVector));
glm::vec3 vector = ... glm::vec3 rezultat = glm::normalize(vector);
Third-person Camera
În cazul camerei de tip Third-person observatorul se mută în jurul unui obiect de interes, ce reprezintă întotdeauna centrul atenției. Deci rotațiile se fac într-un mod diferit
Rotația Camerei Third-person
- se translatează observatorul pe direcția de vizualizare în punctul de interes (target)
- se aplică rotația de tip First-person specifică
- se traslatează observatorul înapoi pe noua direcție de vizualizare cu aceeași distanță
Translația Camerei Third-person
Poziția camerei depinde de poziția punctului de interes. Astfel, mișcarea punctului de interes va determina și translația camerei în mod corespunzător.
Video Laborator 6: https://youtu.be/f7q2TGCRly0
Autor: Anca Băluțoiu
Banda Grafica
Banda Grafica este un lant de operatii executate de procesoarele GPU. Unele dintre aceste operatii sunt descrise in programe numite shadere (eng. shaders), care sunt scrise de programator si transmise la GPU pentru a fi executate de procesoarele acestuia. Pentru a le deosebi de alte operatii executate in banda grafica, pe care programatorul nu le poate modifica, shaderele sunt numite „etape programabile”. Ele dau o mare flexibilitate in crearea de imagini statice sau dinamice cu efecte complexe redate in timp real (de ex. generarea de apa, nori, foc etc prin functii matematice).
Folosind OpenGL sunt transmise la GPU: coordonatele varfurilor, matricile de transformare a varfurilor (M: modelare, V: vizualizare, P: proiectie, MV: modelare-vizualizare, MVP: modelare-vizualizare-proiectie), topologia primitivelor, texturi si ale date.

1. In etapa programabila VERTEX SHADER se transforma coordonatele unui varf, folosind matricea MVP, din coordonate obiect in coordonate de decupare (eng. clip coordinates). De asemenea, pot fi efectuate si calcule de iluminare la nivel de varf. Programul VERTEX SHADER este executat in paralel pentru un numar foarte mare de varfuri.
2. Urmeaza o etapa fixa, in care sunt efectuate urmatoarele operatii:
- asamblarea primitivelor folosind varfurile transformate in vertex shader si topologia primitivelor;
- eliminarea fetelor nevizibile;
- decuparea primitivelor la frontiera volumului canonic de vizualizare (ce inseamna?);
- impartirea perspectiva, prin care se calculeaza coordonatele dispozitiv normalizate ale varfurilor: xd = xc/w; yd = yc/w;zd = zc/w, unde [xc,yc,zc,w] reprezinta coordonatele unui varf in sistemul coordonatelor de decupare;
- transformarea fereastra–poarta: din fereastra (-1, -1) – (1, 1) in viewport-ul definit de programator.
3. Urmatoarea etapa este Rasterizarea. Aceasta include:
- calculul adreselor pixelilor in care se afiseaza fragmentele primitivelor (bucatele de primitive de dimensiune egala cu a unui pixel);
- calculul culorii fiecarui fragment, pentru care este apelat programul FRAGMENT SHADER
- in etapa programabila FRAGMENT SHADER se calculeaza culoarea unui fragment pe baza geometriei si a texturilor; programul FRAGMENT SHADER este executat in paralel pentru un numar mare de fragmente.
- testul de vizibilitate la nivel de fragment (algoritmul z-buffer);
- operatii raster, de exemplu pentru combinarea culorii fragmentului cu aceea existenta pentru pixelul in care se afiseaza fragmentul.
Rezultatul etapei de rasterizare este o imagine memorata intr-un tablou de pixeli ce va fi afisat pe ecran, numit ^^frame buffer^^.
Shader OpenGL
Pentru implementarea de programe SHADER in OpenGL se foloseste limbajul dedicat GLSL (GL Shading Language).
Legarea unui shader la programul care foloseste OpenGL este o operatie complicata, de aceea va este oferit codul prin care se incarca un shader.
Un VERTEX SHADER e un program care se executa pentru FIECARE vertex trimis catre banda grafica. Rezultatul transformarilor, care reprezinta coordonata post-proiectie a vertexului procesat, trebuie scris in variabila standard gl_Position care e folosita apoi de banda grafica. Un vertex shader are tot timpul o functie numita main. Un exemplu de vertex shader:
#version 330 layout(location = 0) in vec3 v_position; // Uniform properties uniform mat4 Model; uniform mat4 View; uniform mat4 Projection; void main() { gl_Position = Projection * View * Model * vec4(v_position, 1.0); }
Un FRAGMENT SHADER e un program ce este executat pentru FIECARE fragment generat in urma operatiei de rasterizare (ce inseamna?). Fragment shader are in mod obligatoriu o functie numita main. Un exemplu de fragment shader:
#version 330 layout(location = 0) out vec4 out_color; void main() { out_color = vec4(1, 0, 0, 0); }
Cum legam un obiect geometric la shader?
Legarea intre obiecte (mesh, linii etc.) si shadere se face prin atribute. Datorita multelor versiuni de OpenGL exista multe metode prin care se poate face aceasta legare. In laborator vom invata metoda specifica OpenGL 3.3 si OpenGL 4.1. Metodele mai vechi nu mai sunt utilizate decat in atunci cand hardware-ul utilizat impune restrictii de API.
API-ul OpenGL modern (3.3+) utilizeaza metoda de legare bazata pe layout-uri. In aceasta metoda se folosesc pipe-uri ce leaga un atribut din OpenGL de un nume de atribut in shader.
glEnableVertexAttribArray(2); glVertexAttribPointer(2, 3, GL_FLOAT, GL_FALSE, sizeof(VertexFormat), (void*)0);
Prima comanda seteaza pipe-ul cu numarul 2 ca fiind utilizat. A doua comanda descrie structura datelor in cadrul VBO-ului astfel:
- pe pipe-ul 2 se trimit la shader 3 float-uri (argument 3) pe care nu le normalizam (argument 4)
- argumentul 5 numit si stride, identifica pasul de citire (in bytes) in cadrul VBO-ului pentru a obtine urmatorul atribut; cu alte cuvinte, din cati in cati octeti sarim cand vrem sa gasim un nou grup de cate 3 float-uri care reprezinta acelasi lucru
- argumentul 6 identifica offsetul inital din cadrul buffer-ul legat la GL_ARRAY_BUFFER (VBO); cu alte cuvinte, de unde plecam prima oara.
In Vertex Shader vom primi atributul respectiv pe pipe-ul cu indexul specificat la legare, astfel:
layout(location = 2) in vec3 vertex_attribute_name;
Mai multe informatii se pot gasi pe pagina de documentatie Vertex Shader attribute index.
- API-ul de OpenGL aici: https://www.opengl.org/sdk/docs/man/
- API-ul pentru GLSL aici: https://www.opengl.org/sdk/docs/manglsl/
Cum trimitem date generale la un shader?
La un shader putem trimite date de la CPU prin variabile uniforme. Se numesc uniforme pentru ca nu variaza pe durata executiei shader-ului. Ca sa putem trimite date la o variabila din shader trebuie sa obtinem locatia variabilei in programul shader cu functia glGetUniformLocation:
int location = glGetUniformLocation(int shader_program, "uniform_variable_name_in_shader");
- shader_program reprezinta ID-ul programului shader compilat pe placa video
- in cadrul framework-ului de laborator ID-ul se poate obtine apeland functia
shader→GetProgramID()sau direct accesand variabila membrushader→program
Apoi, dupa ce avem locatia (care reprezinta un offset/pointer) putem trimite la acest pointer informatie cu functii de tipul glUniform:
//void glUniformMatrix4fv(GLint location, GLsizei count, GLboolean transpose, const GLfloat *value) glm::mat4 matrix(1.0f); glUniformMatrix4fv(location, 1, GL_FALSE, glm::value_ptr(matrix)); // void glUniform4f(GLint location, GLfloat v0, GLfloat v1, GLfloat v2, GLfloat v3) glUniform4f(location, 1, 0.5f, 0.3f, 0); //void glUniform3i(GLint location, GLint v0, GLint v1, GLint v2) glUniform3i(location, 1, 2, 3); //void glUniform3fv(GLint location, GLsizei count, const GLfloat *value) glm::vec3 color = glm::vec3(1.0f, 0.5f, 0.8f); glUniform3fv(location, 1, glm::value_ptr(color));
Functiile glUniform sunt de forma glUniform[Matrix?]NT[v?] (regex) unde:
- Matrix - in cazul in care e prezent identifica o matrice
- N - reprezinta numarul de variabile de tipul T ce vor fi trimise:
- 1, 2, 3, 4 in cazul tipurilor simple
- pentru matrici mai exista si 2×3, 2×4, 3×2, 3×4, 4×2, 4×3
- T - reprezinta tipul variabilelor trimise
- ui - unsigned int
- i - int
- f - float
- v - datele sunt specificate printr-un vector, se da adresa de memorie a primei valori din vector
Comunicarea intre shadere-le OpenGL
In general pipeline-ul programat este alcatuit din mai multe programe shader. In cadrul cursului de EGC vom utiliza doar Vertex Shader si Fragment Shader. OpenGL ofera posibilitatea de a comunica date intre programele shader consecutive prin intermendiul atributelor in si out
Vertex Shader:
#version 330 // GLSL version of shader (GLSL 330 means OpenGL 3.3 API) out vec3 attribute_name;
Fragment Shader:
in vec3 attribute_name;
Mai multe detalii se pot obtine de la: Program separation linkage
Vertex Shader:
#version 410 // GLSL 410 (OpenGL 4.1 API) layout(location = 0) out vec4 vertex_out_attribute_name;
Fragment Shader:
#version 410 layout(location = 0) in vec4 fragment_in_attribute_name;
Video Laborator 7: https://youtu.be/y1st9QxXbn8
Autor: Cristian Lambru
Iluminare folosind GLSL
Lumina este un factor foarte important în redarea cât mai realistă a unei scene 3D. Împreună cu proprietățile de material ale unui obiect, lumina determină modalitatea în care obiectul este afișat în scena 3D.
Există mai multe modele empirice pentru calculul reflexiei luminii într-un punct al unei suprafețe: Phong (1975), Blinn (1977), Oren-Nayar (1994), Cook-Torrance (1981), Lambert (1760), etc (la curs veți discuta despre modelul Lambert, Phong și Blinn).
Modelul Phong pentru calculul reflexiei luminii
Ca model de reflexie vom prezenta în continuare un model care extinde modelul de reflexie Phong și care conține toate cele 4 componente care pot fi folosite pentru a calcula iluminarea. Pentru a obține astfel culoarea într-un punct al unei suprafețe vom avea următoarele componente :
- Componenta emisivă
- Componenta ambientală
- Componenta difuză
- Componenta speculară
Contribuția fiecărei componente este calculată ca o combinație dintre proprietățile de material ale obiectului (factorul de strălucire și de difuzie al materialului) și proprietățile sursei de lumină (culoarea sursei de lumină, poziția sursei de lumină).
Astfel, culoarea finală a luminii într-un punct aparținând unei suprafețe este:
culoare = emisiva + ambientala + difuza + speculara; # GLSL
În cele ce urmează prezentăm pe scurt ce reprezintă cele 4 componente și cum pot fi calculate.
Componenta emisivă
Aceasta reprezintă lumina emisă de un obiect și nu ține cont de nicio sursă de lumină. O utilizare des întâlnită pentru componenta emisivă este aceea de a simula obiectele care au strălucire proprie (de ex: sursele de lumina precum neonul sau televizorul).
Avem astfel:
emisiva = Ke; # GLSL
- Ke – culoarea emisivă a materialului
Componenta ambientală
Aceasta reprezintă lumina reflectată de către obiectele din scenă de atât de multe ori încât pare să vină de peste tot.
Astfel, lumina ambientală nu vine dintr-o direcție anume, apărând ca și cum ar veni din toate direcțiile. Din această cauză, componenta ambientală este independentă de poziția sursei de lumină.
Componenta ambientală depinde de culoarea de material ambientală a suprafeței obiectului și de culoarea ambientală luminii.
Similar componentei emisive, componenta ambientală este o constantă (se poate extinde modelul atribuind fiecărei lumini din scenă o culoare ambientală).
Avem astfel:
ambientala = Ka * culoareAmbientalaGlobala; # GLSL
- Ka – constanta de reflexie ambientală a materialului
- culoareaAmbientalaGlobala – culoarea ambientală a luminii
Componenta difuză
Aceasta reprezintă lumina reflectată de suprafața obiectului în mod egal în toate direcțiile.
Cantitatea de lumină reflectată este proporțională cu unghiul de incidență al razei de lumină cu suprafața obiectului.
Avem astfel: $difuza = K_d \cdot culoareLumina \cdot max(\vec{N}\cdot \vec{L}, 0)$
difuza = Kd * culoareLumina * max (dot(N,L), 0); # GLSL
- Kd - constanta de reflexie difuză a materialului
- culoareLumina – culoarea luminii
- N – normala la suprafață (normalizată)
- L – vectorul direcției luminii incidente (normalizat)
- $max(\vec{N}\cdot \vec{L}, 0)$ – produsul scalar $\vec{N}\cdot \vec{L}$ reprezintă măsura unghiului dintre acești 2 vectori; astfel, dacă $i$ este mai mare decât $\pi/2$ valoarea produsului scalar va fi mai mică decât 0, acest lucru însemnând că suprafața nu primește lumină ( sursa de lumină se află în spatele suprafeței ) și de aici și formula care asigură că în acest caz suprafața nu primește lumină difuză
Componenta speculară
Un reflector perfect, de exemplu o oglindă, reflectă lumina numai într-o singură direcție $\vec{R}$, care este simetrică cu $\vec{L}$ față de normala la suprafață. Prin urmare, doar un observator situat exact pe direcția respectivă va percepe raza reflectată.
Componenta speculară reprezintă lumina reflectată de suprafața obiectului numai în jurul acestei direcții, $\vec{R}$. Acest vector se obține prin:
vec3 R = reflect (-L, N) # GLSL
- Este necesar să se utilizeze -L deoarece
reflect()are primul parametru vectorul incident care intră în suprafață, nu cel care iese din ea așa cum este reprezentat în figură
În modelul Phong se aproximează scăderea rapidă a intensității luminii reflectate atunci când $\alpha$ crește prin $(cos \alpha)^n$, unde $n$ este exponentul de reflexie speculară al materialului (shininess).
După cum se observă, față de celelalte 3 componente, componenta speculară depinde și de poziția observatorului. Dacă observatorul nu se află într-o poziție unde poate vedea razele reflectate, atunci nu va vedea reflexie speculară pentru zona respectivă. De asemenea, nu va vedea reflexie speculară dacă lumina se află în spatele suprafeței.
Astfel avem: $speculara = K_s \cdot culoareLumina \cdot primesteLumina \cdot (max(\vec{V}\cdot \vec{R}, 0))^n$
speculara = Ks * culoareLumina * primesteLumina * pow(max(dot(V, R), 0), n) # GLSL
- Ks - constanta speculară de reflexie a materialului
- V – vectorul direcției de vizualizare (normalizat)
- R – vectorul direcției luminii reflectate (normalizat)
- n – coeficientul de strălucire (shininess) al materialului
- primesteLumina – 1 dacă $\vec{N}\cdot \vec{L}$ este mai mare decât 0; sau 0 în caz contrar
Un alt model de iluminare (Blinn (1977)) pentru componenta speculară se bazează pe vectorul median, notat cu $\vec{H}$. El face unghiuri egale cu $\vec{L}$ și cu $\vec{V}$. Dacă suprafața ar fi orientată astfel încât normala sa să aibă direcția lui $\vec{H}$, atunci observatorul ar percepe lumina speculară maximă (deoarece ar fi pe direcția razei reflectate specular).
Termenul care exprimă reflexia speculară este în acest caz: $(\vec{N} \cdot \vec{H})^n$
pow(dot(N, H), n) # GLSL
- $\vec{H} = (\vec{L} + \vec{V})$ (normalizat)
Atunci când sursa de lumină și observatorul sunt la infinit, utilizarea termenului $\vec{N}\cdot \vec{H}$ este avantajoasă deoarece $\vec{H}$ este constant.
Ținând cont de toate acestea, avem pentru componenta speculară următoarea formulă: $speculara = K_s \cdot culoareLumina \cdot primesteLumina \cdot (max(\vec{N}\cdot \vec{H}, 0)^n $
speculara = Ks * culoareLumina * primesteLumina * pow(max(dot(N, H), 0), n) # GLSL
Atenuarea intensității luminii
Atunci când sursa de lumină punctiformă este suficient de îndepărtată de obiectele scenei vizualizate, vectorul $\vec{L}$ este același în orice punct. Sursa de lumină este numită în acest caz direcțională. Aplicând modelul pentru vizualizarea a două suprafețe paralele construite din același material, se va obține o aceeași intensitate (unghiul dintre $\vec{L}$ și normală este același pentru cele două suprafețe). Dacă proiecțiile suprafețelor se suprapun în imagine, atunci ele nu se vor distinge. Această situație apare deoarece în model nu se ține cont de faptul că intensitatea luminii descrește proporțional cu inversul pătratului distanței de la sursa de lumină la obiect. Deci, obiectele mai îndepărtate de sursă sunt mai slab luminate. O posibilă corecție a modelului, care poate fi aplicată pentru surse poziționale (la distanță finită de scenă) este:
culoareObiect = emisiva + ambientala + factorAtenuare * ( difuza + speculara ); # GLSL
- factorAtenuare = $1/d^2$ este o funcție de atenuare
- $d$ este distanța de la sursă la punctul de pe suprafață considerat
Corecția de mai sus nu satisface cazurile în care sursa este foarte îndepărtată. De asemenea, dacă sursa este la distanță foarte mică de scenă, intensitățile obținute pentru două suprafețe cu același unghi $i$, între $\vec{L}$ și $\vec{N}$, vor fi mult diferite.
- $K_c$ - factorul de atenuare constant
- $K_l$ - factorul de atenuare liniar
- $K_q$ - factorul de atenuare patratic
Modele de shading
De asemenea, există mai multe modele de shading, care specifică metoda de implementare a modelului de calcul al reflexiei luminii. Mai exact, modelul de shading specifică unde se evaluează modelul de reflexie. Dacă vrem să calculăm iluminarea pentru o suprafață poligonală:
- în modelul de shading Lambert, se calculează o singură culoare pentru un poligon al suprafeței
- în modelul de shading Gouraud (1971), se calculează câte o culoare pentru fiecare vârf al unui poligon. Apoi, culorile fragmentelor poligonului se calculează prin interpolare între vârfuri (interpolarea liniară a culorilor vârfurilor, pentru fragmentele de pe laturi și interpolare liniară între culorile capetelor fiecărui segment interior, pentru fragmentele interioare poligonului). Calcularea culorilor vârfurilor se poate efectua în vertex shader.
- în modelul de shading Phong (1975), se calculează câte o normală pentru fiecare vârf al unui poligon. Apoi, pentru fiecare fragment se determină o normală prin interpolare între normalele din vârfuri. Astfel, se calculează o culoare pentru fiecare fragment al unui poligon (în fragment shader)
 Figura 1. Diferite modele de shading: Lambert (o culoare per primitivă), Gouraud (o culoare per vârf), Phong (o culoare per fragment)
Figura 1. Diferite modele de shading: Lambert (o culoare per primitivă), Gouraud (o culoare per vârf), Phong (o culoare per fragment)
În acest laborator se va discuta modelul de shading Gouraud.
Detalii de implementare
Pentru simplitate, în cadrul laboratorului vom implementa modelul de shading Gouraud (în vertex shader):
- Se vor calcula practic doar componentele difuze și speculare așa cum au fost prezentate anterior; componenta emisivă nu va fi folosită iar calculul componentei ambientale va fi simplificat astfel încât să nu mai trebuiască trimis nimic din program către shader (mai multe detalii la punctul 3).
- Vom folosi ca proprietăți de material pentru obiecte doar culoarea de material difuză și speculară (transmise din program către shader) : Ks și Kd.
- În shader vom aproxima lumina ambientală cu o
culoareAmbientalaGlobalacare va fi o constantă în shader, iar în loc de Ka (constanta de material ambientală a obiectului) vom folosi Kd (constanta de material difuză a obiectului). - Culoarea luminii (difuză și speculară) va fi albă, deci culoareLumina va fi 1 și nu va mai fi necesar să fie folosită la înmulțirile din formulele de calcul pentru componentele difuză și speculară.
- Calculele de iluminare se vor face în world space, deci înainte de a fi folosite, poziția și normala vor trebui aduse din object space în world space. Acest lucru se poate face astfel:
- pentru poziție:
vec3 world_pos = (model_matrix * vec4(v_position,1)).xyz;
- pentru normală:
vec3 world_normal = normalize( mat3(model_matrix) * v_normal );
- Vectorul direcției luminii L:
vec3 L = normalize( light_position - world_pos );
- Vectorul direcției din care priveste observatorul V:
vec3 V = normalize( eye_position - world_pos );
- Vectorul median H:
vec3 H = normalize( L + V );
- normalize(V) – normalizează vectorul V
- normalize(V1+V2) – normalizează vectorul obținut prin V1+V2
- normalize(P1-P2) - returnează un vector de direcție normalizat între punctele P1 și P2
- dot(V1,V2) – calculează produsul scalar dintre V1 și V2
- pow(a, shininess) – calculează a la puterea shininess
- max(a,b) – returnează maximul dintre a și b
- distance(P1,P2) – returnează distanța euclidiană dintre punctele P1 și P2
- reflect(V,N) - calculează vectorul de reflexie pornind de la incidenta V și normala N
Video Laborator 8: https://youtu.be/QuhUGAhrXUQ
Autori: Philip Dumitru, Andrei Lăpușteanu, Robert Caragicu
Modelarea reflexiei luminii
Va reamintim formulele pentru calculul culorii intr-un punct al unei suprafețe:
$culoarea = c_e + c_a + c_d + c_s$
Emisiva: $c_e = K_e$
Ambientala: $c_a = I_a \cdot K_a$
Difuza: $c_d = K_d \cdot I_{sursă} \cdot max(\vec{N}\cdot \vec{L}, 0)$
Speculara: $c_s = K_s \cdot I_{sursă} \cdot lum \cdot (max(\vec{N}\cdot \vec{H}, 0)^n $, unde $lum = (\vec{N}\cdot \vec{L}>0) ? 1 : 0$
Dacă introducem mai multe lumini în scenă și ținem cont și de factorul de atenuare, atunci culoarea intr-un punct al unei suprafețe este:
$culoarea = K_e + I_a \cdot K_a + \sum{f_{at_i} \cdot I_{sursă_i} (K_d \cdot max(\vec{N}\cdot \vec{L_i}, 0) + K_s \cdot lum_i \cdot (max(\vec{N}\cdot \vec{H_i}, 0)^n})$
La laboratorul de saptamana trecuta, pentru ușurința implementării, am considerat mai multe simplificări:
- am considerat că toate constantele de material $K_e, K_a, K_d, K_s$, sunt variable de tip float (un singur canal)
- deoarece constantele de material au fost considerate pe un singur canal, s-a introdus variabila uniformă object_color, o variabilă de tip vec3 care a modelat culoarea obiectului
- am considerat că intensitatea sursei de lumină este o constantă float (cu valoarea 1)
- am ignorat culoarea emisă
- am înlocuit constanta de material $K_a$ cu constanta $K_d$ (pentru a trimite mai putine uniforme)
- am considerat intensitatea luminii ambientale o constantă float (cu valoarea 0.25)
Totuși, trebuie să menționăm că modelul complet urmărește formula de mai sus, unde constantele de material $K_e, K_a, K_d, K_s$ sunt diferite și au 3 canale $(R,G,B)$, iar intensitatea luminii ambientale și intensitatea sursei de lumină au de asemenea 3 canale. Expresia luminii se evaluează separat pentru cele trei canale.
Iluminare Phong in Fragment Shader
Modelul de iluminare aplicat in cazul implementarii in fragment shader este acelasi cu cel studiat in Laboratorul 07, din punct de vedere matematic. Totusi, exista o diferenta majora intre cele doua implementari prin faptul ca iluminarea nu se mai aplica la nivelul fiecarul vertex ci la nivel de fragment. Rezultatul final este superior calitativ intrucat iluminarea fiecarui fragment nu se va mai calcula pe baza interpolarii luminii calculate la nivel de vertex ci pe baza normalei si pozitiei in spatiu a fiecarui fragment.
Valorile de intrare primite de fragment shader sunt interpolate linar intre valorile vertexilor ce compun primitiva utilizata la desenare.
Imaginea de mai sus este obtinuta prin desenarea unui triunghi avand cele 3 varfuri de culori diferite: rosu, verde, albastru
Prin transmiterea culorii de la Vertex Shader la Fragment Shader culoarea fiecarui fragment de pe suprafata triunghiului este calculata ca o interpolare linara intre culorile vertexilor ce compun primitiva specificata (in acest caz, un triunghi).
Acelasi procedeu se aplica pentru orice alta proprietate, cum ar fi:
- pozitia in spatiul lume a unui fragment (daca trimitem pozitiile vertexilor)
- normala in spatiul lume a unui fragment (daca trimitem normalele vertexilor)
- orice alta valoarea transmisa de la vertex shader la fragment shader
- etc
API-ul OpenGL permite specificarea modelului de interpolare prin utilizarea unor termeni specifici in cadrul Fragment Shaderului:
- flat - valoarea nu va fi interpolata
- smooth - interpolare perspectiva (implicita)
- noperspective - interpolare liniara in spatiu fereastra
Mai multe detalii despre modelele de interpolare se pot gasi accesind urmatoarele resurse:
Astfel, utilizand valorile interpolate de pozitie si normala (in spatiul lume) putem sa calculam modeul de iluminare Phong pentru fiecare fragment al unei primitive rasterizate, rezultatul final fiind mult superior intrucat prin interpolarea normalelor se obtine o trecere lina intre suprafete adiacente (sunt interpolate normalele de pe muchii), deci si iluminarea finala va oferi impresia unei suprafete netede. Astfel poligoanele componente ale obiectelor nu vor mai aparea vizibil in imagine.
Detalii de implementare
- Se calculeaza world_position si world_normal in Vertex Shader ca in Laboratorul 07
- Se transmit cele 2 valori catre Fragment Shader
- Se aplica calculul luminii (componenta ambientala, difuza, speculara) in Fragment Shader
Pentru a primi valoarea unei variabile de tip uniform este suficient sa declarati respectiva variabila in shaderul in care este necesara. Deci, NU trimiteti valoarea unei variabile de la Vertex Shader la Fragment Shader
// Vertex Shader uniform vec3 light_position;
// Fragment Shader uniform vec3 light_position;
Iluminare Spot-light
Nu toate sursele de lumina sunt punctiforme. Daca dorim sa implementam iluminarea folosind o sursa de lumina de tip spot trebuie sa tinem cont de o serie de constrangeri
Asa cum se poate vedea si in poza pentru a implementa o sursa de lumina de tip spot avem nevoie de urmatorii parametri aditionali:
- orientarea spotului (directia luminii)
- unghiul de cut-off al spotului ce controleaza deschiderea conului de lumina
- un model de atenuare unghiular al luminii ce tine cont valoarea de cut-off a spot-ului
Astfel, punctul P se afla in conul de lumina (primeste lumina) daca conditia urmatoare este indepilita:
float cut_off = radians(30); float spot_light = dot(-L, light_direction); if (spot_light > cos(cut_off)) { // fragmentul este iluminat de spot, deci se calculeaza valoarea luminii conform modelului Phong // se calculeaza atenuarea luminii }
Pentru a simula corect iluminarea de tip spot este nevoie sa tratam si atenuarea luminii corespunzatoare apropierii unghiului de cut-off. Putem astfel sa utilizam un model de atenuare patratica ce ofera un rezultat convingator.
float cut_off = radians(30); float spot_light = dot(-L, light_direction); float spot_light_limit = cos(cut_off); // Quadratic attenuation float linear_att = (spot_light - spot_light_limit) / (1.0f - spot_light_limit); float light_att_factor = pow(linear_att, 2);
Iluminarea suprafețelor folosind mai multe lumini
Pentru a simula mai multe lumini, putem scrie un shader care să calculeze contribuția fiecărei lumini în parte. Pentru a fi ușor să scriem codul de shadere, acesta poate fi modularizat.
În GLSL se pot defini funcții similar ca în limbajul C. Putem scrie o funcție pentru a calcula pentru o sursă de lumină culoarea rezultată din componentele difuze și speculare. Un exemplu de funcție ar fi:
vec3 point_light_contribution(vec3 light_pos, vec3 light_color) { vec3 color; //calculele componentelor difuze si speculare din modelul Phong de iluminare pentru lumina punctiforma. return color; }
Putem accesa orice variabilă globală din orice funcție din cod, inclusiv uniforme. Astfel putem citi în funcția point_light_contribution normala suprafeței primită ca variabilă de intrare la fragment shader și uniformele cu constante de material, fără să le trimitem ca parametri.
Putem specifica ce tip de parametrii are funcția:
inînseamnă că valoarea va fi copiată când se apelează funcția. Funcția poate modifica parametrul cum doreșteoutînseamnă că valoarea nu fi inițializată de apelant și după ce funcția modifică parametrul valoarea va fi copiată în variabila corespunzătoare apelantuluiinoutle combină pe cele două
Cuvintele cheie in, out si inout se scriu înainte de tipul de data al parametrului funcției.
De exemplu, dacă dorim separat contribuția difuză și cea speculară, un exemplu de semnatură de funcție ar fi:
void point_light_contribution(vec3 light_pos, vec3 light_color, out vec3 diffuse_contribution, out vec3 specular_contribution);
Dacă nu se specifică, parametrul este de tip in. Astfel, putem construi funcții ce întorc mai multe valori.
Metoda de declarare și definiție a funcțiilor este similară cu cea din C.
vec3 point_light_contribution(vec3 light_pos, vec3 light_color); void main() { //... } vec3 point_light_contribution(vec3 light_pos, vec3 light_color) { //... }
Nu este permisă recursivitate în GLSL.
Pentru a trimite ușor multe surse de lumină, putem defini vectori de uniforme. De exemplu, pentru a trimite mai multe surse de lumină punctiforme se declară în shader un vector de uniforme:
uniform vec3 point_light_pos[9]; uniform vec3 point_light_color[9];
Pe urmă putem trimite uniformele cu un apel în cod:
glm::vec3 point_light_pos[9]; glm::vec3 point_light_color[9]; GLuint location = glGetUniformLocation(program, "point_light_pos"); glUniform3fv(location, 9, glm::value_ptr(point_light_pos[0])); //glm::value_ptr intoarce adresa de memorie unde se gasesc datele unui vector, matrici etc.
O altă variantă este declararea unei structuri în shader
struct light_source { int type; vec3 position; vec3 color; vec3 direction; }; uniform light_source lights[9];
În GLSL structura este doar o definiție a unei agregări de tipuri de dată. Nu se poate obține locația unei structuri sau a unui vector de structuri. În schimb, putem interoga locația fiecărui membru din fiecare element din vectorul de structuri. De exemplu, se poate găsi locația uniformei lights[0].position.
Următorul cod C++ trimite pozițiile surselor de lumină în shader:
light_source light_sources[9]; //light_source e o structura declarata similar cu cea scrisa in shader. for (int i = 0;i < 9;++i) { std::string name = std::string("lights[") + std::to_string(i) + std::string("].position"); GLuint location = glGetUniformLocation(program, name.c_str()); glUniform3fv(location, 1, glm::value_ptr(light_sources[i].position)); }
Video Laborator 9: https://youtu.be/YS262bweU2Q
Autor: Bogdan Teacă
Introducere
Am invatat in laboratoarele trecute ca, pentru a adauga detalii obiectului nostru, putem folosi culori asociate fiecarui vertex. Pentru a putea crea obiecte detaliate, asta ar insemna sa avem foarte multi vertecsi astfel incat sa putem specifica o gama cat mai variata de culori si ar ocupa foarte multa memorie. Pentru a rezolva aceasta problema se folosesc texturi.
Pentru scopul acestui laborator, o textura este o imagine 2D (exista si texturi 1D si 3D) care este folosita pentru a adauga detalii obiectului. Ganditi-va la textura ca la o bucata de hartie (cu un desen pe ea) care este impaturita peste obiectul 3D. Pentru ca putem adauga oricate detalii vrem intr-o singura imagine, putem da iluzia ca obiectul este foarte detaliat fara sa adaugam vertecsi in plus.
Diferenta intre un obiect texturat si acelasi obiect netexturat este remarcabil de mare din punct de vedere al acuratetei reprezentarii obiectului respectiv:
Maparea texturilor
Pentru a mapa (impacheta) o textura peste un triunghi, trebuie sa specificam in ce parte din textura corespunde fiecare vertex. Asadar, fiecare vertex ar trebui sa aiba asociat un set de coordonate de textura (2D adica glm::vec2) care specifica partea din textura unde isi are locul.
Coordonatele de textura se afla in intervalul $[0, 1]$ pentru axele x si y (in cazul 2D). Coordonatele texturii incep din punctul $(0, 0)$ pentru coltul din stanga jos a imaginii pana la punctul $(1, 1)$ care se afla in coltul din dreapta sus.
Un punct de pe imagine si care este in spatiul $[0,1] \times [0,1]$ se numeste texel, numele venind de la texture element. Dupa cum se poate vedea in imaginea de mai jos, in functie de coordonatele fiecarui vertex al triunghiului, partea din textura care este mapata peste triunghi poate fi diferita:
Adaugarea unei texturi
Pentru a construi o textura in OpenGL avem nevoie in primul rand de pixelii imaginii ce va fi folosita ca textura. Pixelii trebuie fie generati functional, fie incarcati dintr-o imagine, iar acest pas este independent de OpenGL. In laborator, pentru a citi texturi, se poate folosi clasa Texture2D:
Texture2D::Load2D(const char* fileName, GLenum wrapping_mode)
unde wrapping_mode poate fi:
GL_REPEAT: textura se repeta pe toata suprafata obiectuluiGL_MIRRORED_REPEAT: textura se repeta dar va fi vazuta in oglinda pentru repetarile impareGL_CLAMP_TO_EDGE: coordonatele vor fi intre 0 si 1GL_CLAMP_TO_BORDER: asemanator cu clamp to edge, doar ca ceea ce se afla dincolo de marginea imaginii nu mai este texturat.
Pentru a seta manual modul de wrapping al texturii se pot folosi:
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, wrapping_mode); // modul de wrapping pe orizontala glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, wrapping_mode); // modul de wrapping pe verticala
Dupa ce avem pixelii imaginii incarcate putem genera un obiect de tip textura de OpenGL folosind comanda:
unsigned int gl_texture_object; glGenTextures(1, &gl_texture_object);
Similar cu toate celelalte procese din OpenGL, nu lucram direct cu textura ci trebuie sa o asociem unui punct de legare. Mai mult, la randul lor, punctele de legare pentru texturi sunt dependente de unitatile de texturare. O unitate de texturare e foarte similara ca si concept cu pipe-urile pe care trimitem atribute. Setam unitatea de texturare folosind comanda (o singura unitate de texturare poate fi activa):
glActiveTexture(GL_TEXTURE0 + nr_unitatii_de_texturare_dorite);
Iar pentru a lega obiectul de tip textura generat anterior la unitatea de textura activa folosim punctul de legare GL_TEXTURE_2D:
glBindTexture(GL_TEXTURE_2D, gl_texture_object);
Pentru a incarca datele efective in textura folosim comanda:
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, data);
- Primul argument specifica tipul de textura. Daca punem
GL_TEXTURE_2D, inseamna ca aceasta functie va asocia obiectului de tip textura (trecut anterior prinbind) o textura 2D (deci daca avem legate unGL_TEXTURE_1DsauGL_TEXTURE_3D, acestea nu vor fi afectate). - Al 2-lea argument specifica nivelul de mipmap pentru care vrem sa cream imaginea. Vom explica ce este un mipmap pe parcusul laboratorului. Pentru moment, putem sa lasam valoarea aceasta 0.
- Al 3-lea argument specifica formatul in care vrem sa fie stocata imaginea. In cazul nostru este RGB.
- Al 4-lea si al 5-lea argument seteaza marimea imaginii.
- Urmatorul argument ar trebui sa fie mereu 0 (legacy stuff)
- Argumentele 7 si 8 specifica formatul si tipul de date al imaginii sursa.
- Ultimul argument il reprezinta vectorul de date al imaginii.
Asadar: glTextImage2D incarca o imagine definita prin datele efective, adica un array de unsigned chars, pe obiectul de tip textura legat la punctul de legare GL_TEXTURE_2D al unitatii de texturare active la momentul curent, nivelul 0 (o sa luam aceasta constanta ca atare pentru moment), cu formatul intern GL_RGB cu lungimea width si cu inaltimea height, din formatul GL_RGB. Datele citite sunt de tip GL_UNSIGNED_BYTE (adica unsigned char) si sunt citite de la adresa data.
Pentru a va cimenta si mai mult aceste notiuni, gasiti detalii si exemple suplimentare in aceasta postare.
Utilizarea texturii
Pentru a folosi o textura in shader trebuie urmat acest proces:
glActiveTexture(GL_TEXTURE0); glBindTexture(GL_TEXTURE_2D, texture1->GetTextureID()); glUniform1i(glGetUniformLocation(shader->program, "texture_1"), 0); glActiveTexture(GL_TEXTURE1); glBindTexture(GL_TEXTURE_2D, texture2->GetTextureID()); glUniform1i(glGetUniformLocation(shader->program, "texture_2"), 1);
Unitatea de texturare este folositoare in momentul in care vrem sa atribuim textura unei variabile uniforme din shader. Scopul acestui mecanism este de a ne permite sa folosim mai mult de 1 textura in shaderele noastre. Prin folosirea unitatilor de texturare, putem face bind la multiple texturi, atat timp cat le setam ca fiind active.
OpenGl are minim 16 unitati de texturare care pot fi activate folosind GL_TEXTURE0 pana la GL_TEXTURE15. Nu este nevoie sa se specifice manual numarul, devreme ce unitatea de texturare cu numarul X poate fi activata folosind GL_TEXTURE0 + X.
Urmatorul cod este un exemplu de shader ce poate folosi legarea precedenta, unde texcoord reprezinta coordonatele de texturare primite ca atribute in vertex shader si apoi pasate catre rasterizer pentru interpolare:
#version 330 uniform sampler2D texture_1; in vec2 texcoord; layout(location = 0) out vec4 out_color; void main() { vec4 color = texture2D(texture_1, texcoord); out_color = color; }
Multitexturarea este folositare in momentul in care reprezentam un obiect complex din punct de vedere topologic, de exemplu frunze, cu o textura ce are o topologie mult inferioara ca si complexitate (de exemplu un quad). Daca utilizam o asemenea reducere de complexitate, trebuie sa avem o metoda prin care sa putem elimina, la nivel de fragment, acele fragmente care nu sunt necesare (evidentiate in imaginea urmatoare).
Pentru aceasta, putem sa folosim o textura de opacitate (alpha) care ne spune care sunt fragmentele reale, vizibile, ale obiectului. Combinatia de textura de opacitate si textura de culoare este suficienta pentru definirea acestui bambus:
Elementele individuale ale unui vec4 pot fi accesate utilizand numele componentelor:
- Pentru date geometrice: x, y, z, w
- Pentru date legate de culori (red, green, blue, alpha): r, g, b, a
- Pentru date de texturare: s, t, p, q
Pentru a omite desenarea fragmentelor care nu sunt vizibile se foloseste directiva de shader discard.
if (alpha == 0) { discard; }
Filtrare
Coordonatele prin care se mapeaza vertecsii obiectului pe textura nu depind de rezolutia imaginii, ci sunt valori float in intervalul $[0, 1]$, iar OpenGL trebuie sa-si dea seama ce texel (texture pixel) sa mapeze pentru coordonatele date. Pentru a rezolva aceasta problema se foloste filtrarea, care este o metoda de esantionare si reconstructie a unui semnal.
Reconstructia reprezinta procesul prin care, utilizand acesti pixeli, putem obtine valori pentru oricare din pozitiile din textura (adica nu neaparat exact la coordonatele din mijlocul pixelului, acolo unde a fost esantionata realitatea in spatiul post proiectie).
Pentru a face acest proces mai usor, OpenGL are o serie de filtre care pot fi folosite pentru a obtine maparea dorita, iar cele mai des utilizate sunt: GL_NEAREST si GL_LINEAR.
GL_NEAREST (care se mai numeste si nearest neighbor filtering) este filtrarea default pentru OpenGL. Cand este folosit acest filtru, OpenGL selecteaza pixelul al carui centru este cel mai aproape de coordonatele de texturare. Mai jos se pot vedea 4 pixeli unde crucea reprezinta exact coordonatele de texturare. Texelul din stanga sus are centrul cel mai aproape de coordonata texturii si astfel este ales:
GL_LINEAR (cunoscut drept filtrare biliniara) ia valoarea interpolata din texelii vecini ai coordonatei de texturare, aproximand astfel culoarea mai bine. Cu cat distanta de la coordonata de texturare pana la centrul texelului este mai mica, cu atat contributia culorii acelui texel este mai mare. Mai jos putem vedea cum pixelul intors
Se pot folosi filtre diferite pentru cazul in care vrem sa marim imaginea si cand vrem sa o micsoram (upscaling si downscaling). Filtrul se specifica folosind metoda glTexParameteri:
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST); glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
Mipmaps
Imaginati-va cazul in care avem o camera plina cu obiecte ce folosesc aceeasi textura dar se afla in pozitii diferite. Cele care sunt mai indepartate vor aparea mai mici fata de cele care sunt mai apropiate, dar toate vor avea aceeasi textura de rezolutie mare.
Deoarece obiectele care se afla la departare vor folosi probabil doar cateva fragmente din imaginea de baza, OpenGL va intampina dificultati in obtinerea culorii din textura de rezolutie mare deoarece trebuie sa aleaga culoarea care sa poata reprezenta o portiune foarte mare din textura. Comprimarea unei portiuni mari din textura intr-un singur frament poate duce la artefacte visible pentru obiectele mici, pe langa memoria irosita prin folosirea unei texturi mari pentru obiecte mici.
Pentru a rezolva aceasta problema, se foloseste un concept numit mipmap, care este de fapt o colectie de copii ale aceleiasi imagini, unde fiecare copie este de doua ori mai mica decat copia anterioara. Ideea din spatele conceptului de mipmap este destul de simpla: dupa un anumit prag de distanta, OpenGL va folosi o textura mipmap mai mica pentru acel obiect. Fiindca obiectul este la departare, faptul ca rezolutia este mai mica nu va fi observat de utilizator. O textura mipmap arata in felul urmator:
Crearea de texturi mipmaps este destul de anevoioasa de facut manual, asa ca OpenGL poate face tot acest proces in mod automat, folosind functia glGenerateMipmap(GL_TEXTURE_2D); dupa ce am creat textura.
Cand privim un obiect dintr-un anumit unghi, se poate ca OpenGL sa faca schimbarea intre diferite niveluri de texturi mipmap, ceea ce poate duce la artefacte asa cum se vede in imaginea de mai jos :
Exact ca filtrarea normala, este posibil sa folosim filtrare intre diferite niveluri de mipmaps folosind filtrare NEAREST si LINEAR atunci cand se produce schimbarea intre niveluri. Pentru a specifica acest tip de filtru, inlocuim filtrarea anterioara cu urmatoarele 4 optiuni :
GL_NEAREST_MIPMAP_NEAREST: foloseste cea mai apropiata textura mipmap si foloseste interpolare nearest neighbor pentru a alege culoarea.GL_LINEAR_MIPMAP_NEAREST: foloseste cea mai apropiata textura mipmap si foloseste interpolare liniara pentru a obtine culoarea.GL_NEAREST_MIPMAP_LINEAR: interpoleaza liniar intre cele mai apropiate doua texturi mipmap si si foloseste interpolare nearest neighbor pentru a obtine culoareaGL_LINEAR_MIPMAP_LINEAR: interpoleaza liniar intre cele mai apropiate doua texturi mipmap si foloseste interpolare liniara pentru a obtine culoarea.
Exemplu de folosire:
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR_MIPMAP_LINEAR); glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
GL_INVALID_ENUM.