Laboratorul 6: BST si AVL
1. Obiectivele laboratorului
- Intelegerea notiunii de arbore binar de cautare (BST)
- Intelegerea notiunii de arbore binar de cautare echilibrat (AVL)
Structura laboratorului se gaseste in acest link.
2. BST (Binary Search Tree)
BST este un arbore binar cu o structură specială adaptată căutărilor eficiente, având următoarele proprietăți:
- se dă un nod rădăcină (numit si root)
- în subarborele său stâng sunt stocate valori mai mici decât cea din rădăcină
- în subarborele său drept sunt stocate valori mai mari decât cea din rădăcină
Operații specifice BST
- Inserarea/Căutarea/Ștergerea unui element
- Găsirea predecesorului/succesorului unui element
- Afișarea datelor stocate in forma sortată
- Găsirea elementului min/max/al k-lea ca valoare
2.1. Inserarea unui element într-un BST
Operația de inserarea a unui element într-un BST adaugă elementul ca frunza a arborelui, iar mai apoi nodul cu cheia data va fi inserat ca fiu stâng sau drept in așa fel încât sa se respecte proprietatea BST.
Node* newNode(Data data) { Node* node = (Node*)malloc(sizeof(Node)); node->val = data; node->left = node->right = NULL; return node; } Node* insert(Node* node, int key) { // daca (sub)arborele e gol – se creeaza un nod //si se returneaza adresa if (node == NULL) return newNode(key); //altfel se coboara la stanga sau dreapta in arbore if (key < node->val) node->left = insert(node->left, key); else if (key > node->val) node->right = insert(node->right, key); //pointerul node se intoarce nemodificat pe acest return return node; } //nu se adauga elemente egale
2.2. Căutarea unui element într-un BST
- se începe cu rădăcina, daca valoarea căutata este chiar rădăcina - return
- daca valoarea cautata < cea stocata in rădăcină – se caută in subarborele stâng, altfel in cel drept.
- cautarea are loc pana la gasirea elementului sau pana se ajunge la NULL.
Node* search(Node* root, int key) { //daca radacina e null sau s-a gasit elementul if (root == NULL || root->val == key) return root; //daca valoarea stocata in radacina e mai mica decat cheia if (root->val < key) return search(root->right, key); // daca valoarea stocata in radacina e mai mare decat cheia return search(root->left, key); } //daca nu se gaseste nod cu aceasta cheie se returneaza NULL
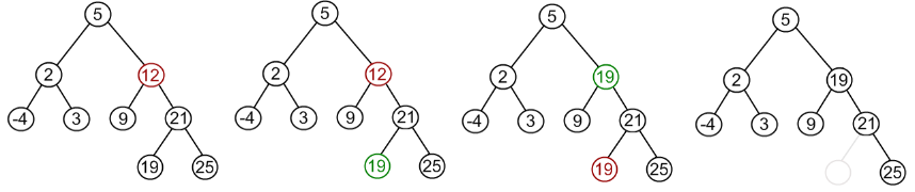
2.3. Ștergerea unui element într-un BST
La partea de ștergere, trebuie avut în vedere:
- Dacă nodul este frunză - se elibereaza spatiul ocupat si se seteaza legatura parintelui catre acel nod cu NULL
- Dacă nodul are doar un subarbore - nodul e scos din arbore și singurul sau copil (subarbore) e legat direct la parintele său (OBS- trebuie actualizat pointerul la stânga sau dreapta din parintele nodului de șters ca să pointeza catre subarborele nodului de șters)
- Dacă nodul are doi subarbori - se bazeaza pe ideea că același set de valori poate fi reprezentat folosind 2 BST diferiți în așa fel încât să ne reducem la unul dintre cele două cazuri de mai sus.
3. AVL (Adelson-Velsky and Landis tree)
Un AVL este un arbore binar de căutare echilibrat.(Proprietatea de echilibru trebuie respectata pentru fiecare nod - înălțimea subarborelui stâng al nodului diferă de inaltimea subarborelui drept al nodului prin cel mult o unitate). De asemenea, trebuie păstrată si condiția de BST.
Arbore binar complet - un arbore binar care este complet umplut cu posibila exceptie a ultimului nivel care este umplut de la stanga la dreapta
OBS! - arborii compleți sau perfecți sunt implicit echilibrați
3.1 Reprezentarea unui nod AVL
typedef int Data; typedef struct N Node; struct N { int height; //inaltimea Data val; // datele efective memorate struct N *left,*right; // legatura catre subarbori };
OBS - înălțimea unui AVL este floor(log N), iar orice cautare/adaugare/stergere/gasire min/max de element se va realiza cu complexitatea O(log N) - cost amortizat pe mai multe operații.
3.2 Inserarea unui nod in AVL
Operația constă în inserția unui nod într-un BST, urmată de reechilibrarea arborelui. Există doua tipuri de rotații (care pastrează proprietatea BST):
- rotație la dreapta
- rotație la stânga
3.2.1 Rotații simple
- RR - x copilul drept al lui y, y copilul drept al lui z
- LL - x este copilul stâng al lui y, y copilul stâng al lui z
3.2.1 Rotații duble
- LR - y e copilul stang al lui z si x e copilul drept al lui y - rotație la stanga + rotație la dreapta
- RL - y e copilul drept al lui z si x e copilul stâng al lui y – rotașie dreapta +rotație stânga











