Laboratorul 01.
În acest laborator ne vom obișnui cu OCTAVE și vom face câteva procesări de semnal simple. Majoritatea tehnicilor de procesare de semnal pot fi executate ca operații pe vectori și matrici, deci OCTAVE este o unealtă foarte folositoare pentru a face aceste operații.
Pentru acest laborator s-a avut ca referință tutorialul (acum am trecut la Octave) de aici
Octave poate fi downloadat de aici: Octave
Urmărind capitolul 1 (Quick Start), haideți să facem următoarele exerciții.
1. Obișnuiți-vă cu mediul de lucru: calea folder-ului (folder path), spațiul de lucru (workspace), istoria, editarea script-ului, consola.
- scrieți a = 2
- scrieți b = 3
- scrieți a+b
- scrieți c=a+b
- scrieți c=a+b; %(notați punctul și virgula ';'). Observați vreo diferență dintre comenzile de mai sus?
- scrieți a*b; %cum puteți afla răspunsul? (hint: variabila 'ans')
2. Vectori
Semnalele pot fi reprezentate ca secvențe de valori, unde în OCTAVE se face, de obicei, prin vectori sau matrici. Să începem cu vectorii.
Pentru a genera un vector de valori date, putem scrie pur și simplu ceva de genul:
- vec1 = [1, 2, 3]; % Notați parantezele drepte '[' și ']' necesare pentru a include valori.
- Creați un vector cu 7 elemente de unu (folosind funcția 'ones'), iar apoi multiplicați-l cu o constantă. Afișați rezultatul.
- Creați un vector de 5 valori aleatoare folosind funcția 'rand'. Introduceți în consolă 'help rand' pentru a găsi cum să o utilizați.
- Indexarea în OCTAVE pornește de la 1, deci puteți selecta primul element din vector folosind comanda vec1(1). De asemenea, puteți indexa părți din vector: vec1(2:3) pentru a selecta un vector format din al doilea și al treilea element din vec1. vec1(end-1:end) selectează ultimele 2 elemente din vec1.
3. Matrici
- Creați o matrice de 5×4 de numere aleatoare (folosind aceeași funcție 'rand' ca mai înainte). Apoi creați o matrice cu elemente de unu de aceeași dimensiune. Acum adunați cele două matrici și afișați rezultatul.
4. Transpusa
Transpusa unei matrici poate fi obținută prin folosirea operatorului `'`.
- Transpuneți matricea pe care ați creat-o mai devreme.
- Creați un vector coloană cu elemente de unu, folosind funcția 'ones' cu un număr de elemente mai mare decât unu pentru prima dimensiune. Printați acest vector.
- Acum transpuneți acest vector și printați-l din nou. Care este diferența dintre afișări?
5. Alte modalități pentru a crea vectori și matrici
- Pentru a crea o secvență continuă (de exemplu de la 1 la 5), putem folosi operatorul (`:'), ca în exemplul v = 1:3 sau v = [1:3].
Creați o secvență de 10 elemente, pornind de la 5.
- Putem face incrementul diferit de 1 și chiar o valoare care nu este întreagă, folosind ceva de genul v = 1:0.5:5. Încercați și vedeți rezultatul. De asemenea, puteți folosi funcția 'linspace' pentru a crea puncte egal distanțate.
- Putem să concatenăm vectorii și matricele între paranteze [], de exemplu a = [1, 2, 3; 4, 5, 6] sau m = [a; b], unde a și b sunt vectori linie de aceeași dimensiune. Creați trei vectori linie de aceeași lungime și concatenați-i ca mai sus pentru a crea o matrice.
- Găsiți ce funcție puteți folosi pentru a determina lungimea și dimensiunea vectorilor și matricelor.
6. Salvarea și încărcarea variabilelor
Verificați funcționalitatea funcțillor 'save' și 'load' (folosind 'help load', 'help save').
- Salvați variabilele pe care le-ați creat, într-un fișiser.
- Ștergeți toate variabilele folosind 'clear';
- Încărcați, din nou, variabiele din fișierul de mai sus.
- Generați o matrice aleatoare de dimensiune 10×10. Salvați doar matricea într-un fișier, iar restul de variabile nu le salvați.
- Ștergeți toate variabilele.
- Încărcați doar matricea.
7. Șiruri de caractere și afișaj
Putem crea într-un mod ușor șiruri de caractere folosind ceva de genul s = 'Hello'.
- Creați o variabilă care să conțină șirul de caractere 'Signal processing'.
- Folosiți funcția 'disp' pentru a afișa acest șir.
- Acum încercați să folosiți funcția 'disp' pentru a afișa un șir care conține 'Lab of ', concatenat cu șirul precedent.
- Acum folosiți funcția 'fprintf' sau 'sprintf' pentru a afișa un șir, urmat de o cifră aleasă de voi.
8. Operații matematice
Operațiile matematice simple pot fi făcute foarte rapid. Puteți să adunați, înmulțiți, ridica la putere sau să inversați matrici: A+B, A*B, A^2, A^-1 sau inv(A). Dacă vreți o operație matematică pentru a fi aplicată element cu element, puteți folosi punctul '.', înainte de operație, de exemplu: A .* B pentru înmulțirea element cu element a fiecărui element din A cu elementul corespunzător din B. Alte funcții, cum ar fi 'sin' pot fi aplicate element cu element pe o matrice: sin(A) este o matrice cu elementele sin($a_{ij}$), unde $a_{ij}$ sunt elementele din A.
9. Funcții
La fel ca în majoritatea limbajelor de programare, o proprietată interesantă este abilitatea de a apela alte funcții.
- Generați un vector aleator folosind 'rand' și găsiți maximul (folosiți funcția 'max').
- Rețineți că OCTAVE a fost dezvoltat pentru a fi folosit pe matrici, deci există multe modalități de a manipula matricele.
- Calculați suma pătratelor elementelor dintr-un vector.
- Puteți parcurge vectorul folosind instrucțiunea 'for'.
x = [1; 2; 3; 4; 5] s = 0; for i = 1 : length(x) s = s + x(i) * x(i); end
- Puteți folosi funcția 'sum'.
s = sum(x .^ 2)
- Folosiți operațiile pe matrici
s = x' * x
x' * x calculează ceea ce se numește produs scalar dintre doi vectori (înmulțirea dintre un vector linie și un vector coloană). Aveți grijă la ordinea operației, pentru că x * x' (vector coloană înmulțit cu vector linie) ne dă o matrice.
10. Grafice
Graficele sunt unele dintre cele mai tari lucruri în OCTAVE, deoarece acestea ne permit să vizualizăm datele noastre.
- Folosiți funcția 'sin' pentru a genera o sinusoidă de frecvență 1 Hz peste 1 secundă (astfel încât ar trebui să obțineți o perioadă completă). Pentru asta trebuie să generați intervalul de timp peste [0 … 1] în pași foarte mici (e.g. 0.01) și apoi să apelați funcția sin(2*pi*f*t) peste această secvență (unde f este frecvența, t este intervalul de timp, iar pi este numărul 3.1415…) pentru a obține sinusoida ca o secvență.
- Verificați funcția 'plot' folosind fie 'help plot', sau chiar mai bine 'doc plot'.
- Plotați sinusoida pe care ați făcut-o mai devreme folosind funcția 'plot'.
- Schimbați culoarea liniei sinusoidei.
- Schimbați tipul liniei sinusoidei.
- Creați altă sinusoidă cu o frecvență diferită (e.g. 2 Hz).
- Afișați ambele sinusoide pe același grafic (pentru aceasta ar trebui să treceți secvențele ca o matrice care conține prima sinusoidă pe primul rând și a doua sinusoidă pe cel de-al doilea rând; sau puteți afișa prima sinusoidă cu 'plot', apoi introduceți comanda 'hold on' și afișați cea de-a doua sinusoidă).
- Încercați să adăugați denumiri axelor X și Y, de asemenea să puneți și titlu figurilor.
- Adăugați o legendă pentru a clarifica care sunt semnalele.
Aici este un exemplu cum ar trebui să arate: 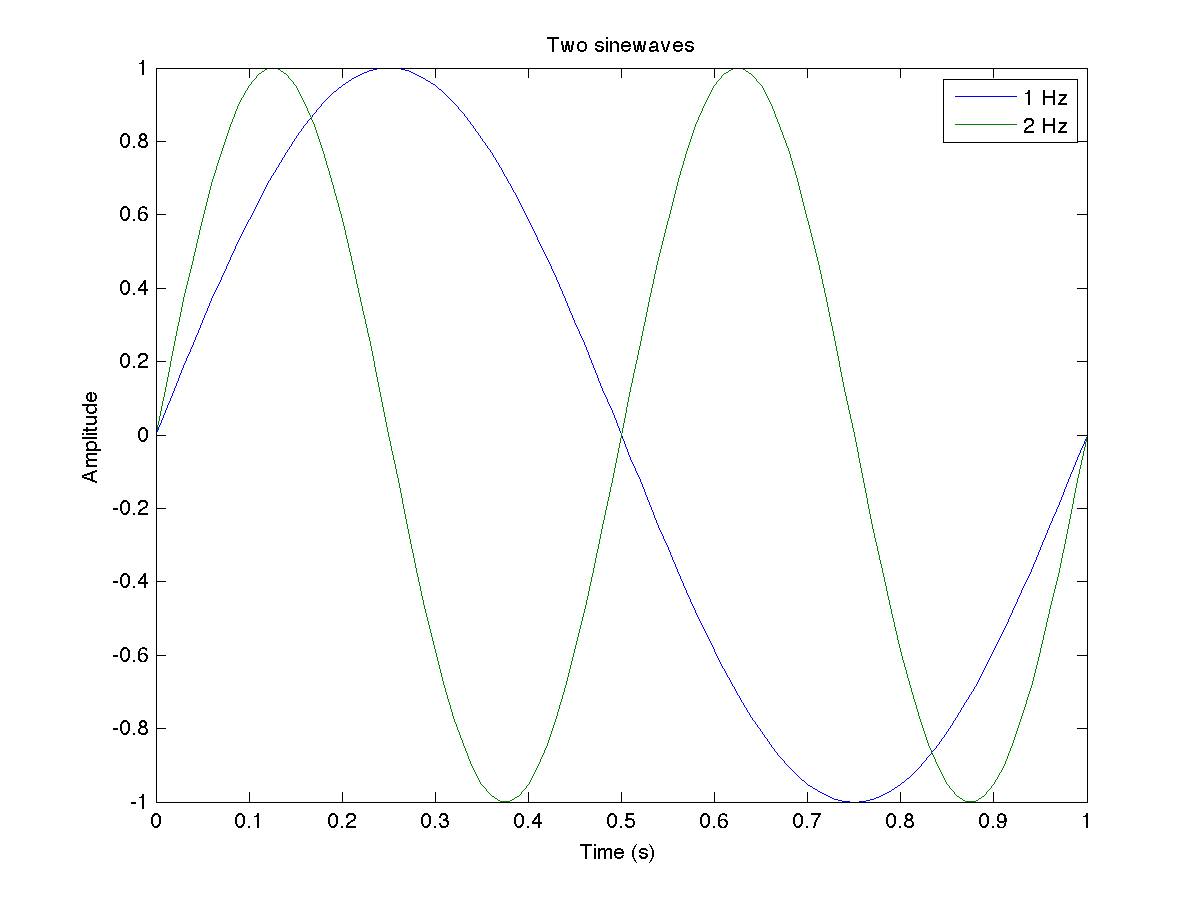
11. Câteva exerciții simple de procesare de semnal
Cel mai bine este să vă faceți programele OCTAVE în script-uri, astfel încât să le puteți reutiliza mai târziu. În acest fel puteți, de asemenea, să vă creați funcții proprii. Pentru acum, haideți să creăm doar niște script-uri.
- Creați un script nou pe care îl numiți 'basic_dsp.m', în care veți scrie comenzile pentru următoarele operații.
După ce aveți câteva comenzi în script îl puteți executa pentru a vedea ce obțineți sau puteți executa doar o parte din el (fie prin selectarea liniilor de interes, comentarea altora, folosind '%', sau folosind secțiuni, via '%%'). Toate lucrurile de mai jos ar trebui să se găsească în script-ul vostru.
- Generați două sinusoide, ca mai devreme, cu diferite frecvențe, dar care acoperă același interval (e.g. 1 Hz și 2 Hz pe o perioadă de 1 secundă).
- Generați un semnal care conține suma celor două sinusoide.
- Afișați aceste trei semnale și verificați diferențele. Hint: folosiți 'figure', înaintea fiecărei comenzi 'plot' pentru a genera trei grafice diferite sau afișați-le pe toate în același grafic (sau în două grafice, unul pentru sinusoida inițială și altul pentru sinusoida rezultată).
Ar trebui să onțineți ceva de genul:
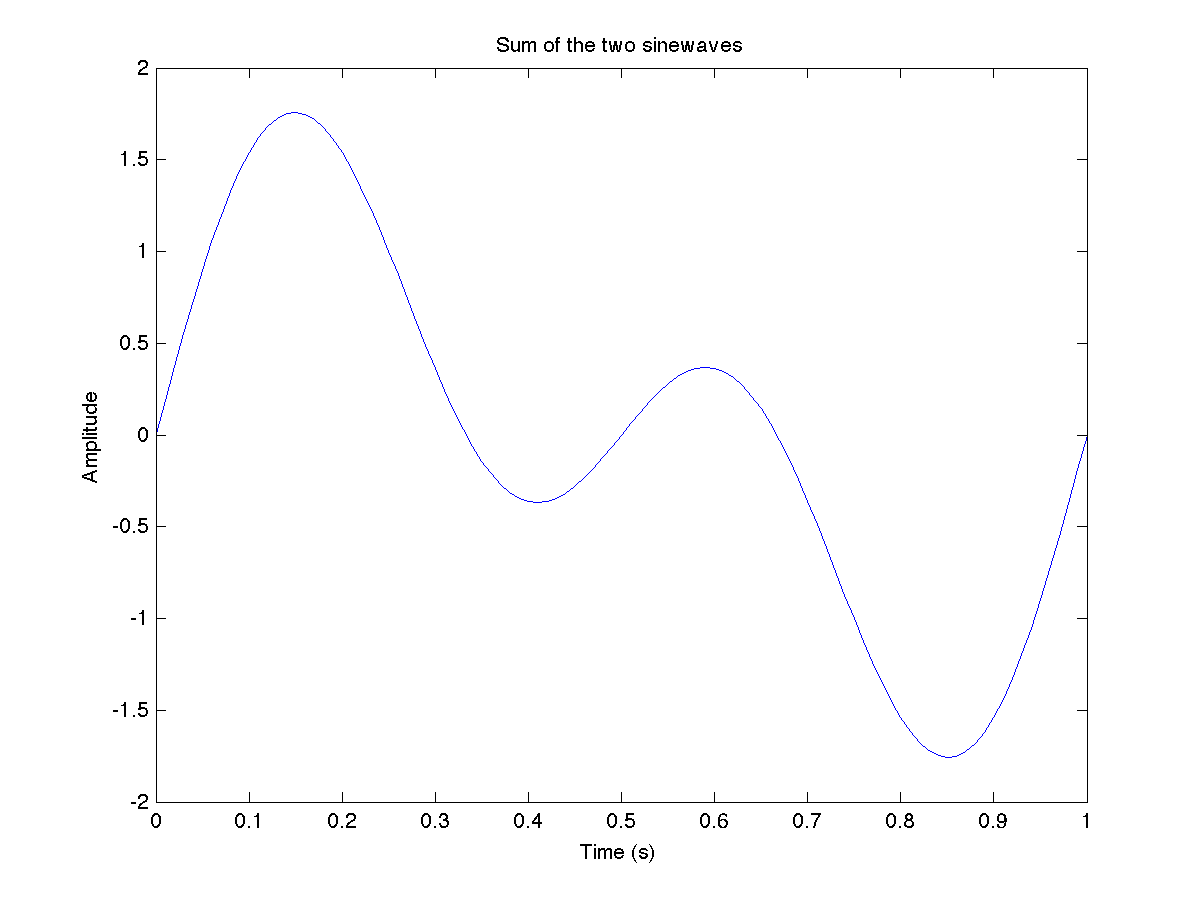
12. O aplicație ușoară
În acest fișier data.mat aveți trei imagini, reprezentate ca matrici tridimensionale (o matrice per culoare - R, G, B). Matricile reprezintă o imagine Img_initial care a fost distorsionată prin adăugarea unui zgomot (matricele R1 și R2), prin formula: IR = Img_initial * 0.3 + R1 * 0.3 + R2 * 0.3
Task-ul vostru este să încercați să reconstruiți matricea originală a imaginii și să o afișați. Pentru asta trebuie să faceți pașii următori:
- încărcați matricile
- afișați cele trei imagini date (matrici) pentru a le vizualiza, folosind funcția 'image', e.g. 'image(R1)'.
- scădeți cumva matricile de zgomot
- afișați imaginea după ce ați eliminat zgomotul
Rețineți că o matrice imagine conține numai valori de la 0 la 255.
13. Column major
OCTAVE stochează datele în ordine pe coloane (column major). Pentru a testa asta încercați să înmulțiți element cu element două matrici mari (N = 1000) folosind 2 for-uri. Parcurgeți matricea pe rânduri, iar apoi pe coloane. Pentru a măsura timpul puneți funcția 'tic' înainte, iar funcția 'toc' după blocul de cod pe care doriți să îl măsurați. De asemenea, calculați înmulțirea folosind operatorul '.*'. Observați diferențele de timp.

