= Tema 2 - Fun with bullets =
Deadline: 03.12.2013
Responsabili: Cristina Ciocan, Paul Urziceanu
Data publicarii: 17.11.2013
Data ultimei modificari: 26.11.2013
* 11:02 24.11.2013
- Am adaugat un punctaj-bonus pe care il gasiti detaliat la sectiunea Punctaj
* 15:18 23.11.2013
- Am modificat checker-ul sa ignore liniile goale.
* 19:54 18.11.2013
- Am modificat DrawManager.java in scheletul de cod.
- Am updatat sa fie aceeasi versiune de checker la sectiunea de resurse ca si pe vmchecker.
* 16:50 18.11.2013
- Am modificat sectiunea cu dilatarea obiectelor si coeficientul pe care trebuie sa-l folositi in tema este 10
- dref(d) = -d/10 - id
* 21:34 26.11.2013
- Amanare deadline pana pe 03.12.2013
- cs.curs picat
- In cazul in care aveti intrebari si nu este forumul functional, ne puteti trimite intrebarile pe e-mail si va vom raspunde cat de repede putem:
- cristina.mihaela.ciocan@gmail.com
- paul.urziceanu@gmail.com
Obiective
- utilizarea corecta a mostenirii si agregarii de clase
- organizarea eficienta a claselor in pachete
- incapsularea datelor si utilizarea modificatorilor de acces
- utilizarea claselor abstracte si/sau a interfetelor
Descrierea problemei
Introducere
Newton, Pitagora si Lagrange organizeaza pentru voi, studentii din anul 2 de la Facultatea de Calculatoare, un turneu de tras cu arma. Insa, pentru a fi totul mai interesant fiecare din cei trei au complicat jocul astfel:
- Pitagora a pus la dispozitie mai multe tipuri de proiectile cu forme geometrice diverse alcatuite din diferite materiale.
- Newton a descris miscarea si traiectoria proiectilelor cu atmosfera si modul in care acestea se corodeaza in contactul cu atmosfera.
- Lagrange a calculat pentru fiecare tip de proiectil cum ar arata conturul produs prin ciocnirea tintei.
Pe scurt, un student are la dispozitie mai multe proiectile pe care le va lansa la diferite momente de timp si de la o anumita distanta catre o suprafata tinta. Cerinta problemei este sa calculati cum va arata aceasta suprafata (numita si ecran in enuntul temei) in urma impactului cu multiplele proiectile lansate.
Tipuri de proiectile
Pitagora, pasionat de geometrie, a propus urmatoarele tipuri de proiectile, fiecare avand o forma specifica la coliziunea cu suprafata tinta:
| id | Tip proiectil | Forma geometrica |
|---|---|---|
| 1 | TriGrapeShot | triunghi |
| 2 | Carcass | patrat |
| 3 | CanisterShot | dreptunghi |
| 4 | ChainShot | triunghi |
| 5 | Shrapnel | patrat |
| 6 | HeatedShot | romb |
| 7 | SpiderShot | dreptunghi |
| 8 | SimpleShell | punct |
Studentul are voie sa traga cu orice proiectil din tabelul de mai sus.
Coroziunea atmosferica
Turneul are loc pe o planeta in care atmosfera este diferita fata de cea de pe Pamant si aceasta corodeaza proiectilele astfel incat dupa o anumita distanta acestea se transforma in alt tip de proiectil. Distanta este dictata de urmatoarea formula dependenta de ora, minutul si secunda in care se face tragerea, precum si id-ul asociat fiecarui proiectil:
did = 42 + (id * id * ora + id * minutul + secunda) % 42
Singurul tip de proiectil care nu se modifica, indiferent de distanta parcursa, este SimpleShell:
d8 = +inf
Newton ne ajuta in acest sens si ne explica care este relatia de rudenie intre tipurile de proiectile:
- TriGrapeShot dupa d1 metri se corodeaza si devine un Shrapnel.
- Carcass dupa d2 metri se corodeaza si devine un HeatedShot.
- CanisterShot dupa d3 metri se corodeaza si devine un HeatedShot.
- ChainShot dupa d4 metri se corodeaza si devine un Shrapnel.
- Shrapnel dupa d5 metri se corodeaza si devine un SpiderShot.
- HeatedShot dupa d6 metri se corodeaza si devine un SpiderShot.
- SpiderShot dupa d7 metri devine un SimpleShell.
Exemplu: Presupunem ca lansam un CanisterShot la ora 00:01:00 si suprafata noastra este la distanta ds. Urmarim urmatorii pasi:
- Vedem in ce se poate transforma CanisterShot:
- CanisterShot → HeatedShot
- HeatedShot → SpiderShot
- SpiderShot → SimpleShell
- Calculam pentru fiecare posibila transformare distanta necesara corodarii proiectilului:
- d3 = 42 + (3 * 3 * 0 + 3 * 1 + 0) = 45
- d6 = 48
- d7 = 49
- d8 = +inf
- Vom obtine urmatoarele cazuri pentru proiectilul nostru initial:
- daca ds < d3 atunci, la impactul cu suprafata, proiectilul va fi devenit CanisterShot, ca atare forma impregnata pe ecran va fi cea corespunzatoare unui CanisterShot (dreptunghi).
- daca ds > d3, dar ds - d3 < d6 atunci, la impactul cu suprafata, proiectilul va fi devenit HeatedShot, iar forma impregnata va fi un romb
- daca ds - d3 > d6, dar ds - d3 - d6 < d7 atunci, la impactul cu suprafata, proiectilul va fi devenit SpiderShot, iar forma impregnata va fi un dreptunghi
- in final, daca ds - d3 - d6 - d7 > 0 , atunci SpiderShot se corodeaza si va deveni un SimpleShell care nu se va mai coroda indiferent cat de mare este ds si pe ecran se va observa un punct.
Traiectoriile caracteristice fiecarui proiectil
Studentul trage de la o anumita distanta d, la un anumit moment de timp t, cu un proiectil, la o anumita pozitie (px, py), pe o tinta dreptunghiulara pe care o vom numi ecran; ecranul are o lungime si o latime caracteristice.
Consideram ca ecranul are dimensiunile ex, ey, iar coordonata (0,0) se afla in coltul din stanga sus al dreptunghiului.
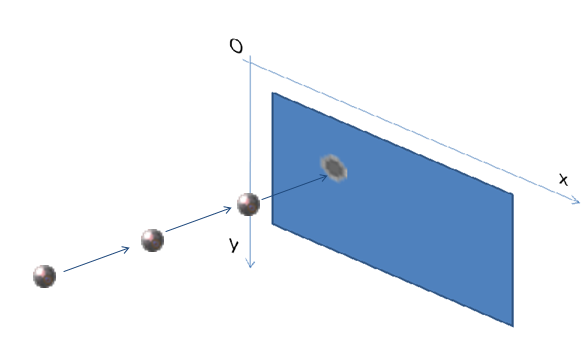
Cand un proiectil loveste ecranul, Newton ne spune ca acesta va lasa forma descrisa de Pitagora pentru fiecare dintre figuri. Asadar, fiecare proiectil are un centru de greutate Cg care, ulterior proiectiei pe ecran, va fi chiar centrul de greutate al figurii 2D reprezentative. Daca studentul trage cu proiectilul la pozitia P = {x,y} atunci inseamna ca, daca ar ajunge nedeviat(vezi sectiunea urmatoare), centrul de greutate al figurii de pe ecran ar fi Cg = P = {x,y} .
Newton insa are cateva observatii de facut cu privire la traiectoriile proiectilelor. In functie de distanta dist parcursa, fiecare dintre proiectilele avand o forma aerodinamica mai ciudata, isi modifica anumite coordonate conform urmatoarelor formule.
Definim dx(dist) si dy(dist) ca fiind deplasarea centrului de greutatea al proiectilului fata de pozitia initiala.
- xf(dist) este pozitia finala pe Ox in functie de distanta parcursa
- yf(dist) este pozitia finala pe Oy in functie de distanta parcursa
xi + dx(dist) = xf(dist)
yi + dy(dist) = yf(dist)
(toate distantele se masoara in metri)
Pentru fiecare proiectil, Newton ne spune modificarile aferente fiecarei axe:
| Tip proiectil | dx | dy |
|---|---|---|
| TriGrapeShot | dist | 0 |
| Carcass | 0 | dist |
| CanisterShot | -dist | 0 |
| ChainShot | 0 | -dist |
| Shrapnel | round(sin(dist * PI / 2)) | 0 |
| HeatedShot | 0 | round(cos(dist * PI / 2)) |
| SpiderShot | round(sin(dist * PI / 2)) | round(cos(dist * PI / 2)) |
| SimpleShell | 0 | 0 |
Exemplu:
Presupunem ca lansam un Carcass la pozitia P = {70,70} pe ecran si la o distanta de 30 de metri fata de acesta.
Distanta la care se corodeaza intr-un HeatedShot este de 65 de metri, insemnand ca acesta atinge ecranul fara sa se transforme in alt tip de proiectil.
Insa, centrul de greutate al figurii proiectate pe ecran nu va fi la
Cg = {70,70},
ci din cauza faptului ca a parcurs 30 de metri, va fi decalat cu
dx = 0 si dy = dist = 30,
deci rezulta Cg = {70,100}.
Putem observa ca un SimpleShell trece nedeviat oricat de multa distanta ar parcurge.
Proiectarea obiectelor pe ecran
Pana in acest moment, stim ca tragem cu un proiectil de la o distanta d fata de ecran la o anumita pozitie p, cunoastem modul in care se corodeaza si implicit cum se transforma fiecare tip de proiectil si stim de asemenea si traiectoria sa in aer, dar trebuie sa vedem cum ajungem sa proiectam figura pe ecran pornind de la pozitia centrului de greutate.
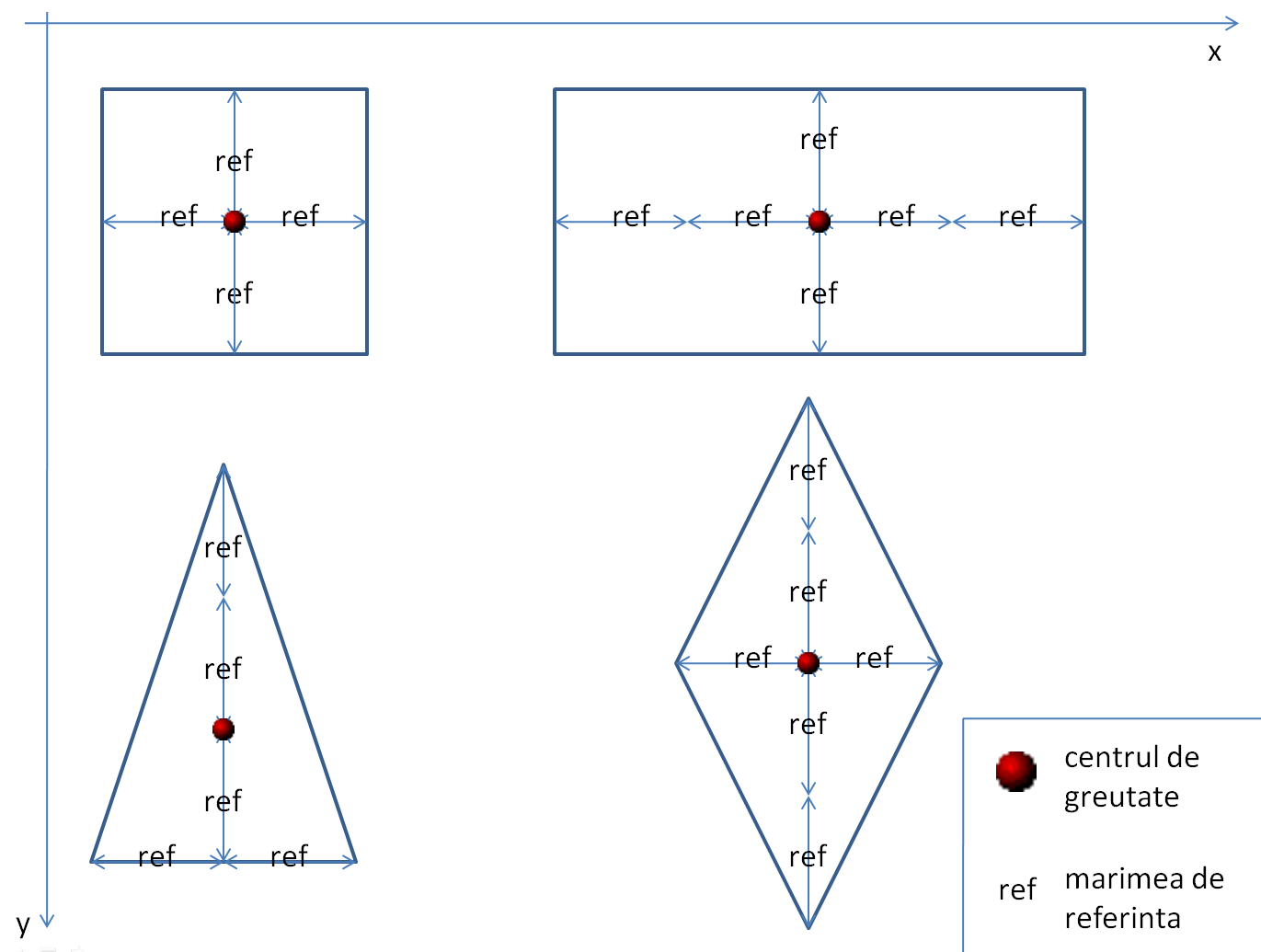
Lagrange vine in ajutor si ne spune ca daca stim care este pozitia centrului de greutate vom putea sa proiectam fiecare figura geometrica (patrat, triunghi, dreptunghi, romb). Pentru simplitate, Lagrange defineste o marime de referinta ref cu ajutorul careia defineste fiecare figura relativ la centrul ei de greutate. Cu alte cuvinte, o figura geometrica este definita pe baza unui centru de greutate, o marime de referinta si o lista de varfuri ale caror coordonate se calculeaza pe baza primelor doua in functie de fiecare figura.
Exemplu:
Presupunem ca a lovit ecranul un proiectil HeatedShot cu Cg = {40,40} si ref = 10.
Forma sa este un romb si are 4 varfuri pe care trebuie sa le determinam. Amintesc ca in stanga sus a ecranului este coordonata {0,0}.
Notam varfurile rombului cu vsus,vjos,vstanga,vdreapta.
vsus = Cg + {0, -2 * ref}vjos = Cg + {0, 2 * ref}vdreapta = Cg + {ref , 0}vstanga = Cg + {-ref, 0}
Afland varfurile, mai trebuie doar sa tragem 4 linii pentru a realiza conturul. In implementarea problemei, veti avea la dispozitie o functie care primeste ca parametru un punct de start, un punct de sfarsit, ecranul pe care sa deseneze si un simbol (descris mai jos), iar aceasta deseneaza o linie intr-o matrice de char-uri ce va reprezenta suprafata voastra.
Fiecare figura geometrica are un simbol asociat (aveti aceste simboluri si in scheletul de cod):
- punct → P
- patrat → S
- romb → R
- dreptunghi → D
- triunghi → T
- iar matricea initiala este formata din caracterul '.', inseamnand pozitie nealterata de impactul cu un proiectil.
Daca 2 linii se intersecteaza, pe ecran va trebui sa apara in acel punct, simbolul caracteristic proiectilului care a ajuns ultimul.
Atunci cand un proiectil se corodeaza si se transforma in alt proiectil, implicit pentru ecran, figura 1 cu Cg1 si ref1 va transfera cele doua caracteristici figurii 2.
Asta inseamna ca:
Cg2 = Cg1ref2 = ref1
Dilatarea dimensiunilor proiectilelor
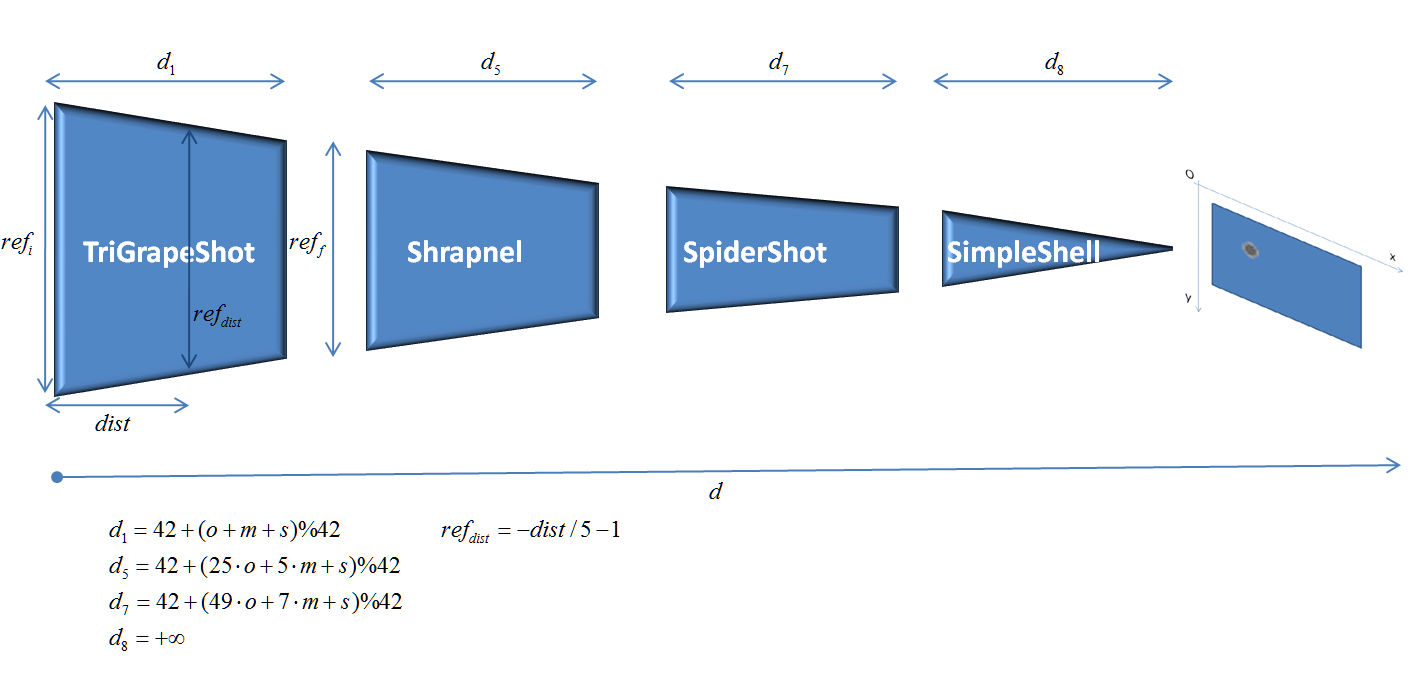
Lansarea proiectilelor se face cu o viteza si o acceleratie extrem de mari, astfel incat Lagrange observa ca, desi noi avem o dimensiune initiala ref, pe parcurs dimensiunile se contracta si evident va scadea si marimea de referinta. Coeficientul de scadere este strict dependent de distanta parcursa, cat si de tipul proiectilului. Asadar, matematicianul ne ofera urmatoarea formula:
refi + dref(dist) = reff(dist)
Modificare
dref(d) = -d/5 - id
dref(d) = -d/10 - id (d este o valoare de tip int deci 4/5 = 0, 9/5 = 1 etc., iar id-ul este cel definit de Pitagora pentru fiecare tip de proiectil)
Se garanteaza ca obiectele sunt destul de mari astfel incat sa nu poata fi micsorate la dimeniuni negative.
Exemplu:
Lansam un TriGrapeShot cu dimensiunea initiala ref = 30 la o distanta dist = 43 de metri de ecranul de dimensiuni dim = {300,300} la pozitia P = {50,50}, la momentul de timp 1:01:00.
Stim ca:
did = 42 + (id * id * ora + id * minutul + secunda) % 42
- TriGrapeShot → Shrapnel → SpiderShot → SimpleShell
- id-urile corespunzatoare sunt 1 → 5 → 7 → 8
d1 = 42 + (id * id * ora + id * minutul + secunda) % 42d1 = 42 + (1 + 1 + 0) % 42 = 44- TriGrapeShot este la 43 de m ceea ce inseamna ca va lovi ecranul fara sa se transforme in Shrapnel. Calculam deplasarile pe axele Ox si Oy:
- dx = dist = 43
- dy = 0
Cg = P + {dx,dy} = {93,50}
Calculam si modul in care se modifica ref:
dref(dist) = -dist/5 - id = -43/5 - 1 = -9ref = ref + dref(dist) = 30 - 9 = 21
Calculam varfurile triunghiului:
vsus = Cg + {0, -2 * ref} = {93, 8}vdreapta = Cg + {ref, ref} = {124,71}vsus = Cg + {-ref, ref} = {72, 71}
Apelam metoda de desenarea a liniei:
- line(vsus,vdreapta,'T',screen)
- line(vsus,vstanga,'T',screen)
- line(vdreapta,vstanga,'T',screen)
Metoda de desenarea a unei linii tine cont si daca punctele sunt pe langa ecran sau daca linia e partial in ecran, asadar nu va trebui sa tratati cazuri de exceptie in acest sens.
Cerinte
Implementati problema descrisa mai sus pornind de la scheletul de cod pus la dispozitie in resurse.
Programul va trebui sa primeasca ca parametru un fisier de intrare “fisier” si sa scrie matricea calculata intr-un fisier cu numele “fisier_out”.
Fisierul de intrare <nume_fisier> va avea urmatoarea forma:
- pe prima linie dimensiunile ecranului: 2 numere ex si ey
- pe a doua linie se va afla un numar
Nce va reprezenta numarul de proiectile ce vor fi lansate spre tinta - urmeaza
Nlinii unde se gasesc pe fiecare linie:- tipul_de_proiectil ref hh:mm:ss dist posx posy
Fisierul de iesire <nume_fisier>_out va avea ey linii si ex coloane reprezentand matricea asociata ecranului pe care se proiecteaza figurile geometrice.
Implementare
Pentru parsarea unei linii din fisierul de intrare, puteti folosi metoda split a clasei String sau puteti utiliza o clasa specializata precum StringTokenizer[2][3].
Pentru operatiile matematice (sin, cos, round), utilizati clasa Math din pachetul util.
Citirea din fisier se poate face in mai multe moduri, insa pentru a nu avea probleme utilizati clasa BufferedInputStream[7] si pentru scriere FileWriter[8].
Insa, puteti utiliza orice alta metoda doriti, conditia este sa functioneze corect.
In scheletul de cod, aveti mai multe pachete, fiecare grupand clasele ce fac parte dintr-o anumita arie. Sugestia este sa cititi cu atentie comentariile pentru fiecare clasa si apoi sa incepeti implementarea efectiva a temei.
In implementare, trebuie sa folositi conceptul de mostenire corect si eficient intocmai cum reiese din enuntul temei. De asemenea, incercati sa evitati cat mai mult codul copiat, sa utilizati specificatorii de acces, precum si cuvantul cheie final atunci cand este cazul.
Pentru orice intrebare legata de scheletul de cod, va rugam sa folositi forumul asociat temei 2.
Pentru a testa tema, va punem la dispozitie checker-ul si testele pe care trebuie sa le treaca tema voastra. (vezi sectiunea Resurse[2])
Precizari
Pentru alte intrebari legate de cerinta, implementare, corectare sau punctare va rog intrebati pe forum-ul asociat temei 2.
Corectare
Tema se va corecta folosind platforma vmchecker [7]. Platforma va rula o suita de teste in cadrul carora implementarile temei vor primi la rulare diferite intrari, iar apoi iesirile generate vor fi comparate cu rezultate asteptate.
Daca platforma de testare nu acorda niciun punct solutiei, atunci acesta va fi punctajul final al implementarii temei.
Neutilizarea mostenirii/agregarii sau a incapsularii intocmai cum sunt sugerate in enunt si in sectiunea de implementare vor duce la acordarea a 0 puncte pe intreaga tema.
Punctaj
80p - acordate de vmchecker pentru executia cu succes a suitei de teste 10p - acordate de asistent pe baza calitatii implementarii si a respectarii principiilor POO 10p - acordate de asistent pe baza lizibilitatii codului, a calitatii comentariilor si a fisierului Readme 10p bonus - acordate de catre asistent pe baza implementarii mostenirii descrise in enunt (daca avem lantul de transformari A→B→C, atunci aceasta sa fie si ierarhia de mostenire din cadrul rezolvarii)
Resurse
UPDATE 7:47 18.11.2013
Am modificat DrawManager pentru a desena cu linii continue.
UPDATE 10:36
Modificare pentru a desena in mod unic o linie indiferent care capat este primul dat ca parametru.
- [1] Schelet
UPDATE 15:22 23.11.2013
Am modificat checker-ul sa ignore liniile goale la compararea de output-uri.
UPDATE 7:47 18.11.2013
Am modificat checker-ul sa aiba testele corecte pentru testele trigonometrice precum cele de pe vmchecker.
- [2] Checker
Am pus un link doar cu DrawManager.java pe care trebuie sa-l copiati in locul celui vechi.
- [3] DrawManager.zip
Referinte
- [1] vmchecker
- [4] java.lang.Math
- [5] JavaArgs