Lab 12 - Machine Learning Security
Objectives
- learn about the vulnerabilities of deep learning models to adversarial samples
- learn to craft adversarial samples that manipulate a deep neural network into producing desired outputs
- generate an image which tricks this deep neural network: https://isc-lab.api.overfitted.io/
- Gandalf prompt injection challenge!
Background
This laboratory discusses the security aspect with regard to Deep Neural Networks (DNNs) and their robustness to specific attacks. Since everyone relies on them for various important tasks, it is imperative to underline that they're not always predictable or reliable and therefore can be manipulated by attackers with sufficient knowledge.
As many of you already know, DNNs are popular nowadays and can efficiently solve a multitude of problems such as face detection or face recognition (think Apple's Face ID). Ideally, each of these tasks can be expressed as a mathematical function which receives as parameters the pixels in the image (their RGB values) and outputs the result we're interested in - e.g., the value 1 if there's a face in the photo or 0 if there isn't. Since we don't know how to write these functions manually, we use DNNs to approximate them via training by knowing pairs of inputs and expected outputs - this is pretty much like interpolation in the sense that the DNN learns to generalize and operate on newer, unseen input data.
Overall this approach achieves good results in automating tasks from various fields and seems very promising.
But…
Problem #1
Since their training methodology relies on minimizing the overall error between the generated outputs and the expected outputs for a given dataset by employing gradient descent, they tend to also learn unusual / purely numeric features which might not always make sense to us. This happens because the whole optimization / training process works with purely numeric information (i.e., gradients) and doesn't have to “justify” specific decisions as long as they match the outputs in the training set. Think of the situation in which such a model incorrectly identifies a face (of a person) in a photo: we can clearly tell, by looking, that there's no face there but the model still claims, according to its identified features, that it found something.
Moreover, the training is usually performed on a discrete set of inputs while the actual input distribution is continuous. This is a fancy sentence so let's look at a more concrete case.
Example: you're training some approximator (such as a neural network) to predict the values of log(x) for a (discrete) set of 5 points in your training set. So your model takes [1, 2, 4, 8, 16] as inputs and must output [0, 1, 2, 3, 4] – which it does! But when you start picking values from a specific interval, e.g., between 8 and 16, the results look pretty bad.
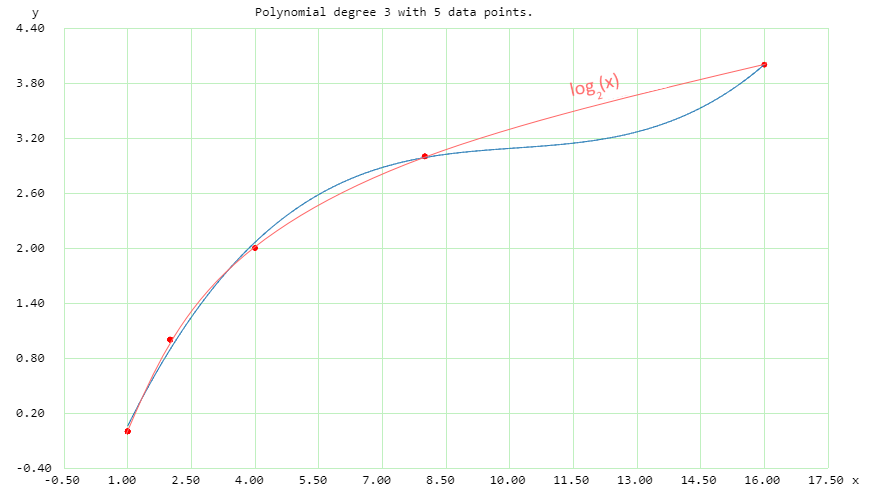
Conclusion: during the training, the approximator's parameters were tuned to minimize the error for the points you provided; but this doesn't mean that it also captures all the specifics of the log() function. So you'd get unexpected results for some of the points. This is an easy example where the errors are discoverable by plotting; in more complex tasks there are many more parameters (and implicitly more than 2 dimensions) so the problems are more difficult to spot.
Problem #2
Neural networks don't know how to say: I don't know. The problem here is especially visible at classifiers; a classifier is a model which tries to map an input to a specific class. See below a diagram of a classifier which maps photos of faces to a set of names.
Classifiers are trained with clearly defined purposes and with a limited number of classes therefore having a limited number of possible outputs. A classifier which is trained with the purpose of identifying human faces has probably never seen cats or dogs in its training data thus producing possibly unexpected behaviour in this scenario. Unlike the classifier, we, as humans, rely on a more “global” knowledge when identifying people or objects in images.
Example: you've trained a DNN which learns to identify Bob, Ben and Alice by looking at photos of their faces. It does the job. Now, someone comes up and provides as input a photo of a cat. The classifier must output something and can only pick between Bob, Ben and Alice (because it wasn't trained to acknowledge the existence of other entities).
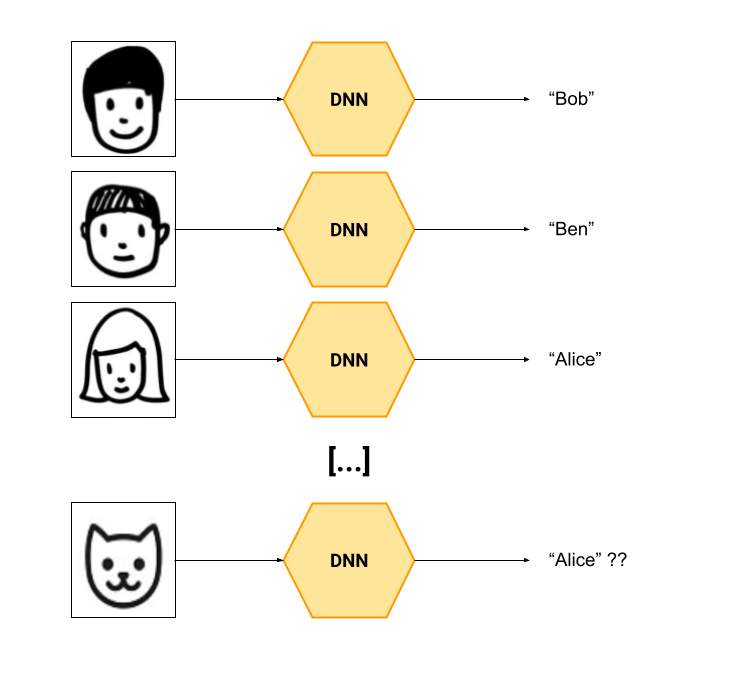
Conclusion: while the classifier can output, besides the most probable class, a confidence value (which indicates how sure it is of its prediction), that value is not always very relevant because the model discriminates only between Bob, Ben and Alice. We can pretty much say that the classifier expects one of the three known faces and doesn't even know that cats exist or what they look like.
Now let's dive into the training part…
Gradient Descent
As previously said, a DNN is pretty much a complex function; to optimize its parameters during training a technique called gradient descent is employed.
This technique tries to minimize the error (or loss) - let's name this function E() - between the predicted output (y_pred) generated by your DNN (let's call it f()) and the known (correct) output (y_true). So, the training would go as follows:
- use the DNN to generate a prediction from an input: y_pred = f(x)
- compute: loss = E(y_pred, y_true)
- tweak the parameters of f() so the loss will be smaller the next time (so the output is more accurate)
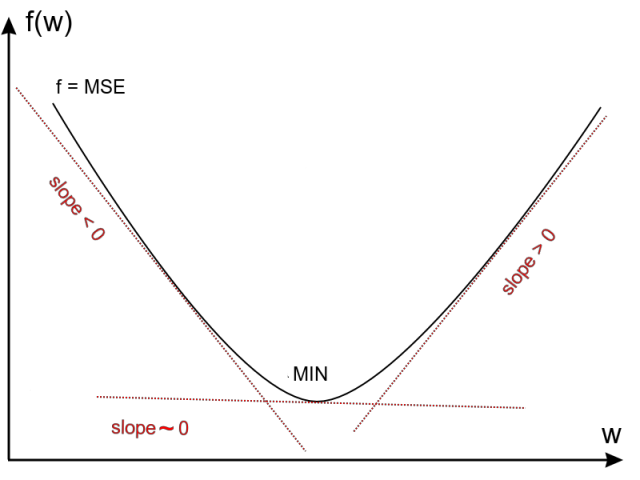
This is done by computing the derivative of E(f(x), y_true) with respect to each parameter (w) from your DNN (f()) while keeping the inputs fixed. Consider that f() does the following: f(x) = w1 * x1 + w2 * x2 + …. Each w is adjusted using its derivative.
Why the derivative? Because it can indicate, with its sign, in which direction (either increase or decrease) you should change the value of w so that the error function E() will decrease.
Generating Adversarial Inputs
Now… what happens if you use gradient descent to… tweak inputs (x) instead of adjusting DNN's parameters (w)? You can pretty much generate an input that manipulates the DNN to generate a desired output.
Exercises
1. DNN adversarial training
This task can be solved using Google Colab (so you don't have to install all the stuff on your machines). You'll have a concrete scenario in which you must fill some TODOs and generate fancy adversarial samples for a DNN.
- you'll have to clone / duplicate it in order to save changes.
2. [BONUS] Prompt Injection
Gandalf has many secrets and he won't easily tell them to anyone! Can you make him spill them?
And BEWARE: any algorithm you ask the LLM to execute, the results won't be exact (due to the low quantization of the model), so you might need to correct them or even change your approach entirely (e.g., sometimes it cannot correctly compute an ASCII to hexadecimal transformation)! More advanced levels use input/output filtering using various mechanisms, so you'll need to bypass them, too!


