Prolog: Jocul Carcassonne
Obiective
- Aplicarea programării logice în limbajul Prolog.
- Utilizarea mecanismelor de găsire automată a tuturor soluțiilor pentru un scop.
Observații preliminare
Tema propune implementarea câtorva mecanisme din mecanica jocului de societate Carcassonne.
Tema este împărțită în 2 etape:
- una pe care o veți rezolva după laboratorul 10, cu deadline în ziua laboratorului 11 (12 pentru seria CB)
- una pe care o veți rezolva după laboratorul 11, cu deadline în ziua laboratorului 12 (și la o săptămână după ziua laboratorului 12, pentru seria CB).
Deadline-ul depinde de semigrupa în care sunteți repartizați. Restanțierii care refac tema și nu refac laboratorul beneficiază de ultimul deadline, și anume în zilele de 19.05, respectiv 26.05.
Rezolvările tuturor etapelor pot fi trimise până în ziua laboratorului 12 (deadline hard pentru toate etapele) (o săptămână după laboratorul 12 pentru seria CB). Orice exercițiu trimis după un deadline soft se punctează la jumătate. Cu alte cuvinte, nota finală pe etapă se calculează conform formulei: n = (n1 + n2) / 2 (n1 = nota obținută înainte de deadline; n2 = nota obținută după deadline). Când toate submisiile preced deadline-ul, nota pe ultima submisie constituie nota finală (întrucât n1 = n2).
În fiecare etapă, veți valorifica ce ați învățat în săptămâna anterioară și veți avea la dispoziție un schelet de cod, cu toate că rezolvarea se bazează în mare măsură pe etapele anterioare. Enunțul caută să ofere o imagine de ansamblu atât la nivel conceptual, cât și în privința aspectelor care se doresc implementate, în timp ce detaliile se găsesc direct în schelet.
Perspectivă generală
Carcassonne (după orașul din sudul Franței) este un joc de societate (boardgame) în care jucătorii își construiesc propriile teritorii, folosind piese pătrate ce conțin pe ele drumuri, cetăți, și pajiști. Jucătorii adună puncte în funcție de cum au plasat piesele și pe ce piese au plasat omuleți. Un joc de Carcassonne în desfășurare arată ca mai jos. Pentru o introducere succintă în esența jocului, vedeți aici - mai ales pasul 1 din partea a 2-a.
În această temă ne vom ocupa în principal de:
- cum putem reprezenta piesele de Carcassonne și, mai târziu, o tablă de joc
- cum putem potrivi piesele și cum putem găsi o poziție unde se potrivește o piesă de pus în joc
- cum putem calcula punctele unui jucător
Pentru simplitate, în temă vom lucra doar cu o parte din piese față de jocul standard adevărat. Vom lucra cu aceste 16 piese:
Piesa 1:  Piesa 2:
Piesa 2:  Piesa 3:
Piesa 3:  Piesa 4:
Piesa 4: 
Piesa 5:  Piesa 6:
Piesa 6:  Piesa 7:
Piesa 7:  Piesa 8:
Piesa 8: 
Piesa 9: 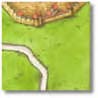 Piesa 10:
Piesa 10: 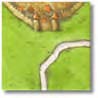 Piesa 11:
Piesa 11:  Piesa 12:
Piesa 12: 
Piesa 13:  Piesa 14:
Piesa 14:  Piesa 15:
Piesa 15:  Piesa 16:
Piesa 16: 
[imaginile de la https:%%//%%wikicarpedia.com/index.php/Base_game_(1st_edition) ]
Astfel, vom avea următoarele restricții față de jocul adevărat:
- avem numai piese cu cetăți, drumuri, și pajiști.
- nu vom avea piese cu scut, și nici piese cu mânăstire.
- pentru modul de punctare al jucătorilor, relevant în etapa 2, este important că:
- pe o piesă pot apărea maxim 2 cetăți diferite;
- vom considera că dacă pe o piesă există mai mult de 2 margini cu drumuri, atunci toate drumurile sunt drumuri diferite (sunt atâtea drumuri câte sunt margini cu drumuri).
Etapa 1
În etapa 1 ne interesează reprezentarea pieselor, rotirea pieselor, și potrivirea unei piese.
Veți lucra numai în fișierul ccs.pl.
Reprezentare
Ne interesează să putem reprezenta cele 16 piese de mai sus. Reprezentarea este la alegerea voastră, ea va fi accesată prin diversele predicate pe care le aveți de implementat. Este doar necesar ca:
- fiecare piesă să aibă o reprezentare diferită, și
- reprezentarea piesei să nu fie direct derivată din numărul ei;
- să puteți reprezenta și fiecare rotație a unei piese, dacă produce o configurație diferită de poziția originală (de exemplu, la piesa 16, toate rotațiile produc aceeași configurație).
Puteți alege ce reprezentare doriți, folosind liste, tupluri, sau alți compuși, acestea putând fi și imbricate, dacă doriți.
Aveți de implementat următoarele predicate în Prolog, documentate și în sursă:
tile(Index, Tile)– acest predicat obține înTilereprezentarea voastră pentru piesa cu indiceleIndexdin lista celor 16 piese.- Așteptarea este ca pentru acest predicat să scrieți 16 reguli, câte una pentru fiecare piesă, fără condiții.
- Reprezentarea nu va fi procesată la testare. Ea va fi doar dată ca argument altor predicate scrise de voi.
- Înainte să decideți asupra reprezentării, citiți ce aveți de făcut la celelalte predicate, ca să știți ce elemente aveți nevoie să aveți în reprezentarea unei piese.
- Testare: Predicatul
tile/2este testat într-un singur test, implementați măcarat/3pentru ca testarea să aibă sens.
at(Tile, Direction, What)– predicatul primește înTileo reprezentare a unei piese și întoarce înWhatce se află pe muchia din direcțiaDirection, care este una dintre nord - sud - est- vest. Pe o muchie putem avea cetate, drum sau pajiște.- De exemplu, interogarea
tile(2, T), at(T, s, X)trebuie să legeXla valoaread, iar interogareatile(2, T), at(T, w, X)trebuie să legeXla valoareac(la fel și pentru direcțiilenșie. - Similar, interogarea
tile(9, T), at(T, n, X)leagăXlac, interogareatile(9, T), at(T, e, X)leagăXlap, iar interogareatile(9, T), at(T, s, X)leagăXlad(și la fel și pentru direcțiaw) - Puteți utiliza predicatul
directions/1dinutils.plpentru a lega o variabilă la lista de direcții.
atL((Tile, Directions, What)– predicatul verifică că la toate direcțiile din lista Directions se află același tip de entitateWhat(e.g. pe toate muchiile respective se află cetate.hasTwoCitadels(Tile)– verifică dacă pe piesă sunt 2 cetăți diferite sau este una singură. Piesele 4 și 5 au două cetăți diferite.
Veți putea testa implementarea predicatelor tile, at, atL și ccw, pe lângă teste, și folosind predicatul printTile din utils.pl. De exemplu, puteți apela interogarea
tile(5, T), printTile(T).
Predicatul printTile produce o reprezentare text a unei piese, folosind simbolul + pentru cetate, linii pentru drumuri, simbolul O pentru intersecții de drumuri, și . pentru colțurile libere ale unei piese.
De exemplu, pentru o implementare corectă până acum, pentru piesa 9, afișarea arată astfel:
.+++. + - \ . | .
Pentru piesa 3:
.++++
+++
+++
+
. .
Și pentru piesa 16:
. | . | --O-- | . | .
Rotire
Trebuie să putem roti piesele pentru a avea mai multe variante de plasare a lor pe tablă. Rotirea unei piese va produce o reprezentare diferită, ca și cum ar fi o piesă nouă. De exemplu, pentru piesa 2 avem următoarele rotiri în sens trigonometric:
Piesa 2 originală:  Piesa rotită 1 dată:
Piesa rotită 1 dată: 
Piesa rotită de 2 ori:  Piesa rotită de 3 ori:
Piesa rotită de 3 ori: 
La rotirea unei piese, reprezentarea trebuie să se schimbe corespunzător. De exemplu, dacă la piesa 2 original aveam drum spre sud și cetate în rest, piesa 2 rotită de 3 ori în sens trigonometric va avea drumul spre vest și va fi afișată ca:
.++++ +++ - +++ +++ .++++
Trebuie implementate predicatele:
ccw(Tile, Rotation, RotatedTile)care leagăRotatedTilela reprezentarea pieseiTilerotită deRotationori în sens trigonometric, cuRotationîntre 0 și 3 inclusiv.rotations(Tile, RotationPairs)care leagăRotationPairsla perechi rotație - piesă-rotită cu toate rotirile diferite ale piesei. De exemplu, piesele 5, 6 și 14 au doar 2 rotiri diferite, iar piesa 16 are doar una.
Potrivire
Pentru ca două piese (eventual rotite) plasate una lângă alta să se potrivească, trebuie ca pe muchia lor comună să aibă aceeași entitate – cetate, drum, sau pajiște. Atunci când o piesă este plasată în joc, trebuie să se potrivească cu toate piesele cu care se învecinează la nord, est, sud, sau vest.
Trebuie implementate predicatele:
match(Tile, Neighbor, Direction)este adevărat dacă piesaTilese potrivește cu o piesăNeighborplasată pe direcțiaDirection. De exemplu, piesa 2 se potrivește la sud cu piesa 16, la vest cu piesele 3, 4, sau 8, și la nord cu piesele 5 sau 6. Dar, bineînțeles, se potrivește la nord și cu oricare dintre piesele 1-12 rotite de 2 ori, și la sud cu oricare dintre piesele 8, 9, 13, 15, 15 rotite de 3 ori. Astfel, de exemplu, este adevărat:tile(2, T2), ccw(T2, 2, T2R2), tile(11, T11), ccw(T11, 3, T11R3), match(T2R2, T11R3, n).findRotation(Tile, Neighbors, Rotation)leagăRotationla un număr între 0 și 3 inclusiv, semnificând e câte ori ar trebui rotită piesaTileîn așa fel încât să se potrivească cu toți vecinii, specificați prin perechi pisă - direcție.- nu uitați că Prolog caută automat soluții în funcție de condițiile care sunt puse pentru un scop.
Etapa 2
În etapa 2 ne vom concentra pe reprezentarea și lucrul cu o tablă de joc și pe plasarea pieselor în joc. Veți lucra tot în fișierul ccs.pl, unde trebuie să existe deja predicatele din prima etapă.
Jocul Carcassonne începe cu plasarea unei piese undeva pe masă, și apoi cu plasarea altor piese. În afară de prima piesă, orice altă piesă trebuie plasată lângă (având o muchie comună) una sau mai multe piese deja plasate pe masă, și trebuie să se potrivească cu toate piesele vecine deja plasate pe masă. Vedeți acest clip, cu mențiunea că noi ne vom ocupa doar de plasarea pieselor, nu și de plasarea omuleților sau de calculul punctelor.
Reprezentarea tablei
Trebuie să vă construiți o reprezentare pentru starea tablei de joc. Această reprezentare trebuie să conțină piesele aflate pe masă (în reprezentarea construită la etapa 1) și pozițiile lor, în coordonate carteziene.
În predicatele de mai jos, pozițiile vor fi perechi (X, Y). Notați că pozițiile sunt relative la o piesă arbitrară, și putem avea și coordonate negative.
Aveți de implementat predicatele de mai jos, cu observația că trebuie să implementați cel puțin primele 3 predicate pentru a putea testa:
emptyBoard(Board)- leagăBoardla reprezentarea unei mese goale, fără piese.boardSet(BoardIn, Pos, Tile, BoardOut)- leagă BoardOut la rezultatul plasării pe tablaBoarda pieseiTilela pozițiaPos. FolosițicanPlaceTile(vezi mai jos) pentru a verifica dacă plasarea este validă.boardGet(Board, Pos, Tile)- leagăTilela piesa de pe pozițiaPospe tablaBoard.boardGetLimits(Board, XMin, YMin, XMax, YMax)- leagă ultimele 4 argumente la coordonatele minime/maxime ale pieselor de pe tablaBoard.
Hint: ca să puteți testa parțial tema, implementați inițial boardSet fără verificarea validității mutării.
Ca să puteți verifica predicatele de mai sus, puteți folosi printBoard/1 din utils.pl, folosind interogări de tipul (vedeți predicatul boardTiles/2 din testing.pl pentru valori de indecși):
boardSetTest(Index, Board), printBoard(Board).
Predicatul printBoard/1 afișează și coordonatele pe margini, cu coordonatele x mai mici în dreapta și cu coordonatele y mai mici în jos. De exemplu, pentru tabla cu indexul 1 în teste – corespunzând cu zona din centru-dreapta în imaginea de mai sus, afișarea este:
-1 0 1 2
.+++.
+
1
+
.+++.
. .. .+++++. .
++ +++++++
+++++++++++++++ 0
++++ ++ ++
.++++. .. | .. .
.+++. . | .
+ \
----- - -1
. . . .
Plasarea pieselor
Pentru plasarea corectă a pieselor pe tablă, trebuie implementate predicatele:
canPlaceTile(Board, Pos, Tile)- întoarce adevărat dacă piesaTilese poate plasa la pozițiaPospe tablaBoard(vedeți sursa pentru lista de condiții).getAvailablePositions(Board, Positions)- leagă Positions la lista de poziții disponibile pentru a plasa piese.findPositionForTile(Board, Tile, Position, Rotation)- găsește pentru piesaTileo poziție și o rotație în așa fel încât să se potrivească cu piesele existente pe tablaBoard. Predicatul întoarce ca soluții diferite toate posibilele plasări ale piesei pe tablă.
Testare
Pentru testare folosiți predicatele check sau vmcheck.
Testele se află în fișierul testing.pl. Tipurile testelor sunt descrise succint la începutul fișierului. Pentru a verifica un test, puteți face interogarea în consolă cu scopurile plasate (de obicei) între ghilimele în primul argument.
Pentru rezultate mai detaliate ale testării, puteți decomenta linia %detailed_mode_disabled :- !, fail. din fișierul testing.pl. Atenție! În acest caz, este posibil ca punctarea să fie diferită decât rezultatul de pe vmchecker, unde linia este comentată.
Resurse
Changelog
- 19.05 – corecție a testului canPlaceA|a
- 18.05 – clarificare necesitate prima etapă; îmbunătățire afișare teste cu mulțimi
- 17.05 (seara) – testele pentru etapa 2, mici corecții în comentarii și enunț, mai ales observații despre poziții
- 17.05 – etapa 2 publicată (fără teste)
- 16.05 – pus la loc linia pentru activarea modului de testare detaliat din
testing.pl - 15.05 – corecție observație legată de printTile
- 14.05 – Clarificare intersecții
- 14.05 – Îmbunătățire teste (pentru ca implementări triviale să nu treacă testele)
- 9.05 – upload inițial.
- 9.05 – clarificare reprezentare
- 9.05 – adăugare etichete teste


