Haskell: Graph Zoo

• Data publicării: 12.04.2022
• Data ultimei modificări: 04.05.2022
• Deadline hard: ziua laboratorului 10
• Forum temă
• vmchecker

• Aplicarea mecanismelor funcționale, de tipuri (inclusiv polimorfism) și de evaluare leneșă din limbajul Haskell.
• Exploatarea evaluării leneșe pentru decuplarea conceptuală a prelucrărilor realizate.

Tema urmărește familiarizarea cu două modalități de reprezentare a grafurilor orientate, una standard (prin mulțimi de noduri și de arce) și alta constructivă (algebrică), adecvată unei abordări funcționale. Veți avea ocazia să implementați diverse operații de manipulare a grafurilor sub ambele reprezentări, astfel încât să puteți compara punctele lor tari și slabe.

Tema este împărțită în 3 etape:

• una pe care o veți rezolva după laboratorul 7, cu deadline dependent de ziua în care aveți laboratorul:
  • laborator marți ⇒ deadline 26 aprilie
  • laborator miercuri ⇒ deadline 27 aprilie
  • laborator joi ⇒ deadline 28 aprilie
  • laborator vineri ⇒ deadline 29 aprilie
  • laborator luni ⇒ deadline 2 mai
• una pe care o veți rezolva după laboratorul 8, cu deadline la o săptămână după deadline-ul etapei 1
• una pe care o veți rezolva după laboratorul 9, cu deadline la o săptămână după deadline-ul etapei 2.

Așa cum se poate observa, ziua deadline-ului variază în funcție de semigrupa în care sunteți repartizați. Restanțierii care refac tema și nu refac laboratorul beneficiază de ultimul deadline (deci vor avea deadline-uri în zilele de 02.05, 09.05, 16.05).

Rezolvările tuturor etapelor pot fi trimise până în ziua laboratorului 10 (deadline hard pentru toate etapele). Orice exercițiu trimis după un deadline soft se punctează cu jumătate din punctaj. Cu alte cuvinte, nota finală pe etapă se calculează conform formulei: n = (n1 + n2) / 2 (n1 = nota obținută înainte de deadline; n2 = nota obținută după deadline). Când toate submisiile sunt înainte de deadline, nota pe ultima submisie este și nota finală (întrucât n1 = n2).

În fiecare etapă, veți folosi ce ați învățat în săptămâna anterioară pentru a dezvolta aplicația.

Pentru fiecare etapă există un schelet de cod (dar rezolvarea se bazează în mare măsură pe rezolvările anterioare). Enunțul caută să ofere o imagine de ansamblu atât la nivel conceptual, cât și în privința aspectelor care se doresc implementate, în timp ce detaliile se găsesc direct în schelet.

În această etapă:

• veți lucra cu una dintre reprezentările standard ale grafurilor orientate, bazată pe mulțimi de noduri și arce
• veți defini funcții de manipulare a acestei reprezentări și veți implementa câțiva algoritmi uzuali.

Construcțiile și mecanismele de limbaj pe care le veți exploata în rezolvare sunt:

• liste, pentru reprezentarea ordinii nodurilor într-o parcurgere etc.
• mulțimi, pentru unicitatea nodurilor și a arcelor într-un graf, pentru verificarea facilă e egalității a două grafuri, fără a ține cont de ordinea nodurilor și a arcelor etc.
• funcționale, atât pe liste, cât și pe mulțimi, ocazie cu care veți vedea conceptul în acțiune și pe alte structuri decât listele standard
• list comprehensions, unde le veți considera utile
• evaluare leneșă, implicită în Haskell, pentru decuplarea conceptuală a construcției unei structuri de parcurgerea acesteia.

În schelet veți găsi două module:

• StandardGraph: conține reprezentarea grafului orientat și funcții de acces și manipulare:
  • tipul StandardGraph a, deja definit ca pereche între o mulțime de noduri și una de arce
  • funcția fromComponents construiește un graf pe baza nodurilor și arcelor
  • funcțiile nodes și edges întorc cele două mulțimi de mai sus
  • funcțiile outNeighbors și inNeghbors întorc mulțimile de vecini înspre care ies, respectiv dinspre care intră arce către nodul curent
  • funcția removeNode înlătură un nod și toate arcele sale din graf
  • funcția splitNode sparge un nod în mai multe noduri, ținând cond de arcele nodului inițial
  • funcția mergeNodes îmbină mai multe noduri într-unul singur, ținând cont de arcele nodurilor inițiale
• Algorithms: conține algoritmii standard de căutare, BFS și DFS:
  • funcțiile bfs și dfs întorc lista de noduri parcurse în ordinea aferentă căutării în lățime, respectiv în adâncime, pornind de la un anumit nod, ținând cont și de posibilele cicluri. Aceste funcții vor fi derivate dintr-o funcție mai generală, menționată în continuare
  • funcția search generalizează cele două strategii de căutare de mai sus, plecând de la observația că singura diferență dintre ele este modul în care se combină la un moment dat nodurile deja existente în structura de date utilizată (stivă/coadă, ambele reprezentate ca liste standard) cu vecinii proaspăt expandați ai nodului curent. Funcția nu este testată direct.
  • funcția countIntermediate verifică existența unei căi între două noduri din graf, și calculează numărul nodurilor intermediare pe care le expandează cele două strategii de mai sus pentru acest scop.

Găsiți detalii despre funcționalitate și implementare, precum și exemple, direct în codul sursă. Veți avea de completat definițiile care încep cu *** TODO ***.

Pentru reprezentarea mulțimilor, veți folosi tipul predefinit Set a, similar tipului listă [a]. Având în vedere că există funcții pe mulțimi cu același nume ca cele pe liste (de exemplu, map, filter), pentru evitarea conflictului de nume, abordarea standard, adoptată și în temă, este de a importa etichetat modulul necesar (import qualified Data.Set as S), urmând ca toate tipurile și funcțiile din acest modul să fie utilizate cu numele prefixat: S.Set a, S.map, S.filter etc.

ATENȚIE! Toate funcțiile din această etapă, cu excepția search, vor fi implementate FĂRĂ recursivitate explicită. Nerespectarea acestei cerințe va conduce la o depunctare de 10p/100 per funcție.

Este suficient ca arhiva pentru vmchecker să conțină modulele StandardGraph și Algorithms.

În această etapă:

• veți lucra cu o altă reprezentare a grafurilor orientate, pe care o vom denumi constructivă, sau algebrică (explicațiile urmează)
• veți redefini funcțiile de acces și manipulare din etapa 1 (din modulul StandardGraph), pentru a opera pe noua reprezentare
• pentru bonus, veți începe să implementați o funcționalitate de compactare a reprezentării unui graf, continuată în etapa 3.

Funcțiile din modulul Algorithms ar trebui să funcționeze neschimbate în etapa 2, cu toate că accentul nu mai cade pe ele acum.

Construcțiile și mecanismele noi de limbaj pe care le veți exploata în rezolvare, pe lângă cele din etapa 1, sunt:

• tipurile de date utilizator.

Ce putem înțelege prin reprezentare algebrică a grafurilor? Ori de cât ori auzim aceste termen, ne putem gândi la construirea unor obiecte mai complexe din altele mai simple, în baza unor operații de îmbinare. De exemplu, plecând de la numerele 0 și 1, și utilizând operațiile de adunare și înmulțire, putem genera toate numerele naturale.

Similar, putem elabora o abordare constructivă a grafurilor orientate, pornind de la următoarele mecanisme (vedeți articolul din secțiunea de Referințe dacă doriți să aprofundați subiectul):

• graful vid, fără noduri și fără arce, denumit Empty
• graful cu un singur nod, denumit Node x, unde x este eticheta nodului
• graful obținut prin reunirea nodurilor și a arcelor din alte două grafuri, denumit Overlay g1 g2, unde g1 și g2 sunt alte grafuri
• graful obținut prin reunirea nodurilor și a arcelor din alte două grafuri, precum și prin conectarea exhaustivă a tuturor nodurilor din primul graf cu cele din al doilea, denumit Connect g1 g2, unde g1 și g2 sunt alte grafuri.

Ideile de mai sus se pot traduce direct într-un tip de date utilizator, unde a este tipul etichetelor nodurilor:

data AlgebraicGraph a
    = Empty
    | Node a
    | Overlay (AlgebraicGraph a) (AlgebraicGraph a)
    | Connect (AlgebraicGraph a) (AlgebraicGraph a)

Mai jos, sunt exemplificate mai multe grafuri care utilizează această reprezentare, pentru o înțelegere mai bună:

• Overlay (Node 2) (Node 3) este un graf foarte simplu, care conține doar nodurile 2 și 3, fără niciun arc.
• Connect (Node 2) (Node 3) conține nodurile 2 și 3, precum și arcul (2, 3).
• Connect (Node 1) (Overlay (Node 2) (Node 3)) conține nodurile 1, 2 și 3, și arcele (1, 2) și (1, 3), pentru că nodul 1 trebuie conectat cu fiecare dintre nodurile 2 și 3.
• Connect (Node 1) (Connect (Node 2) (Node 3)), conține nodurile 1, 2 și 3, și arcele (1, 2), (1, 3) și (2, 3).
• Connect (Node 1) (Connect (Node 2) (Connect (Node 3) (Node 4))) conține nodurile 1, 2, 3 și 4, și arcele (1, 2), (1, 3), (1, 4), (2, 3), (2, 4) și (3, 4), întrucât fiecare nod trebuie conectat cu toate arcele care îi urmează.

Din exemplele de mai sus, transpar două avantaje importante ale acestei reprezentări algebrice, care îi lipsesc reprezentării standard din etapa 1:

• Se împiedică direct prin construcție definirea unor grafuri inconsistente, fără a fi necesare verificări suplimentare. De exemplu, în etapa 1, puteam defini un graf prin mulțimea de noduri [1] și mulțimea de arce [(1, 2)], fără a preciza nodul 2 în mulțimea de noduri. În reprezentarea algebrică este imposibilă definirea unui astfel de graf.
• Anumite grafuri dense, ca în ultimul exemplu de mai sus, care necesită un spațiu pătratic în raport cu numărul de noduri în cazul enumerării explicite a arcelor, pot fi reprezentate în spațiu liniar în cazul algebric.

În baza celui de-al doilea avantaj de mai sus, se poate pune problema compactării reprezentării unui graf, analizând relațiile pe care nodurile le au cu celelalte noduri. Spre exemplu, pentru unul dintre grafurile exemplificate mai sus, este dată și o reprezentare alternativă (a doua), mai lungă.

• Connect (Node 1) (Overlay (Node 2) (Node 3))
• Overlay (Connect (Node 1) (Node 2)) (Connect (Node 1) (Node 3)).

Ca fapt divers, echivalența celor două reprezentări de mai sus poate fi înțeleasă ca distributivitate a lui Connect față de Overlay.

Compactarea reprezentării grafului se bazează pe conceptul de descompunere modulară. Pe scurt, un modul este o mulțime de noduri, care toate au aceeași mulțime de out-neighbors și aceeași mulțime de in-neighbors dacă ne uităm doar în afara modulului, cu toate că cele două mulțimi pot fi diferite. Nodurile din interiorul unui modul pot fi conectate oricum. Se poate demonstra că, în cazul a două module disjuncte, dacă există un arc orientat între un nod din primul modul și un nod din al doilea, atunci există arce cu orientarea respectivă între toate nodurile din primul modul și toate nodurile din al doilea (exact ce exprimă Connect).

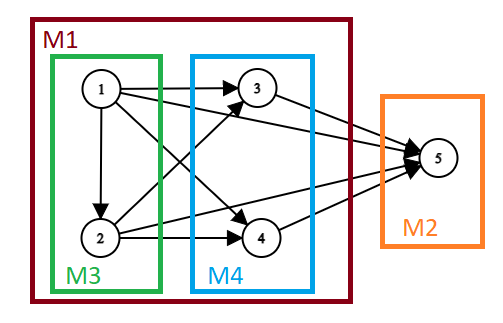
În graful de mai jos, observăm următoarele:

• La cel mai înalt nivel, se disting două module, M1 și M2, întrucât avem arce de la fiecare nod din M1 către fiecare (unicul) nod din M2. Toate nodurile din M1 au aceeași mulțime de out-neighbors [5], și aceeași mulțime de in-neighbors, [], în exteriorul lui M1. Aceeași proprietate se respectă banal și pentru nodul 5 din M2.
• Dacă ne concentrăm acum doar asupra lui M1, observăm că acesta poate fi la rândul său descompus în două module, M3 și M4, întrucât avem arce de la fiecare nod din M3 către fiecare nod din M4. Arcul (1, 2) nu este relevant, pentru că nodurile din interiorul unui modul pot fi conectate oricum.
• Mulțimea [1, 3] nu ar putea constitui un modul, pentru că există arcul (1, 2), dar nu și arcul (3, 2).

Orice graf are două descompuneri modulare banale:

• un singur modul cu întregul graf
• câte un modul pentru fiecare nod,

dar acestea sunt neinteresante. Pe noi ne interesează descompunerile nebanale, dacă acestea există, care contribuie la compactarea reprezentării grafului. De exemplu, cea mai compactă reprezentare a grafului din imagine este:

Connect (Connect (Connect (Node 1) (Node 2))
                 (Overlay (Node 3) (Node 4)))
        (Node 5)

Veți implementa aspecte legate de descompunerea modulară parțial ca bonus, în cadrul etapelor 2 și 3. Deși există algoritmi eficienți (liniari) pentru determinarea descompunerii modulare, aceștia sunt destul de complicați, astfel că vom utiliza o abordare mai simplă bazată pe forță brută. Cu alte cuvinte, vom genera toate partițiile mulțimii de noduri, și apoi le vom filtra pentru a obține modulele.

În etapa 2, scheletul conține următoarele module:

• StandardGraph: implementat în etapa 1. Reprezentarea originală este de pereche de mulțimi de noduri, respectiv arce. Ca încălzire:
  • Gândiți-vă cum se poate redefini tipul StandardGraph ca tip de date utilizator (data), în locul sinonimului de tip pereche.
  • Funcțiile nodes și edges pot fi definite direct drept câmpuri în cadrul tipului.
  • Funcția fromComponents trebuie și ea redefinită.
  • Schițați în comentarii redefinirea celor patru entități de mai sus. Această parte nu este testată automat, dar o veți prezenta.
  • Nu este necesar să reimplementați celelalte funcții din acest modul.
• AlgebraicGraph: conține reprezentarea algebrică a grafurilor, descrisă mai sus
  • Tipul AlgebraicGraph este cel prezentat mai sus.
  • Mai departe, veți implementa aceleași funcții ca în modulul StandardGraph, cu excepția fromComponents, dar de data aceasta vor opera pe reprezentarea algebrică.
  • Toate funcțiile vor fi implementate CU recursivitate explicită.
  • Veți observa că implementările funcțiilor removeNode, splitNode și mergeNodes respectă un tipar similar, pe care vom căuta să îl generalizăm în etapa 3.
  • ATENȚIE! Funcțiile de mai sus trebuie să opereze direct pe reprezentarea algebrică din această etapă. NU este permisă convertirea în reprezentarea din etapa 1 și utilizarea funcțiilor de acolo.
• Modular: conține momentan doar câteva funcții pentru determinarea descompunerii modulare a grafului, dar va fi îmbogățit în etapa 3:
  • Funcția mapSingle este asemănătoare cu map, în sensul că aplică o funcție asupra fiecărui element al unei liste, dar aplicarea se face asupra unui singur element din listă la un moment dat, celelalte rămânând nemodificate.
  • Funcția partitions generează toate partițiile unei liste.

În această etapă:

• veți continua să lucrați cu reprezentarea algebrică a grafurilor, cu care v-ați familiarizat în etapa 2
• veți înzestra reprezentarea cu funcționalități standard (de exemplu, de descriere sub formă de șir de caractere sau de verificare a egalității), utilizând instanțe de clase
• veți defini anumite funcționale pe grafuri, pentru a observa cum funcționalele pe liste pot fi generalizate, întrucât ele surprind tipare universale de prelucrare a structurilor
• veți redefini anumite funcții din etapa 2 pentru a utiliza funcționalele de mai sus
• în cea mai mare parte pentru bonus, veți continua să implementați funcționalitatea de compactare a reprezentării unui graf, începută în etapa 2.

Construcțiile și mecanismele noi de limbaj pe care le veți exploata în rezolvare, pe lângă cele din etapa 2, sunt:

• polimorfismul ad-hoc și clasele.

Ca încălzire, amintiți-vă că ați operat până acum cu două reprezentări ale grafurilor, StandardGraph și AlgebraicGraph, și că ați implementat același set de funcții de acces și manipulare pentru amândouă (nodes, edges etc.). Gândiți-vă cum ați putea generaliza această interfață de lucru cu grafuri în Haskell:

• Cum ați defini o clasă care să surprindă conceptul de graf orientat? Ați parametriza-o cu tipul concret (de exemplu, AlgebraicGraph a) sau cu constructorul de tip în sine (de exemplu, AlgebraicGraph)?
• Cum ar arăta tipul funcției nodes dacă ar fi definită în interiorul acestei clase?

Schițați răspunsul în comentarii în vederea prezentării (partea aceasta nu este testată automat).

În etapa 3, scheletul conține următoarele module:

• AlgebraicGraph
  • Funcțiile nodes, edges, outNeighbors, inNeighbors sunt cele din etapa 2.
  • Instanța clasei Num permite interpretarea unei expresii aritmetice ca un graf algebric, în care literalii numerici sunt etichete de noduri, iar adunarea și înmulțirea reprezintă operațiile Overlay, respectiv Connect. De exemplu, graful din diagrama de mai sus poate fi reprezentat prin expresia aritmetică ((1*2) * (3+4)) * 5.
  • Instanța clasei Show permite descrierea grafului sub forma unui șir de caractere, utilizând perspectiva aritmetică de mai sus.
  • Instanța clasei Eq permite verificarea corectă a egalității dintre două grafuri algebrice, ținând cont că același graf conceptual poate avea două descrieri simbolice diferite.
  • Funcția extend permite elaborarea unui graf, prin atașarea unor subgrafuri oarecare în locul nodurilor, în baza unei funcții de corespondență. Funcția extend constituie baza implementării tuturor operațiilor de mai jos.
  • Funcția familiară splitNode va fi reimplementată utilizând extend.
  • Instanța clasei Functor, prin operația fmap, generalizează funcționala map de pe liste pe grafuri, permițând aplicarea unei funcții pe toate etichetele nodurilor dintr-un graf. Implementarea va utiliza extend.
  • Funcția familiară mergeNodes va fi reimplementată utilizând fmap.
  • Funcționala filterGraph generalizează funcționala filter de pe liste pe grafuri, pentru a păstra doar nodurile ale căror etichete satisfac o proprietate. Implementarea va utiliza extend.
  • Funcția familiară removeNode va fi reimplementată utilizând filterGraph.
• Modular
  • Funcțiile mapSingle și partitions sunt cele din etapa 2.
  • Funcția isModule verifică dacă o mulțime candidat de noduri constituie într-adevăr un modul (vedeți explicațiile din etapa 2).
  • Funcția isModularPartition verifică dacă o partiție candidat este într-adevăr modulară, i.e. dacă toate submulțimile sunt module.
  • Funcția maximalModularPartition determină cea mai acoperitoare partiție, pornind de la lista tuturor partițiilor mulțimii de noduri (vedeți explicațiile din comentarii).
  • Funcția modularlyDecompose este deja implementată, și vă permite să puneți cap la cap funcțiile de mai sus.

• Încercați să folosiți pe cât posibil funcții predefinite din modulele Data.List și Data.Set. Este foarte posibil ca o funcție de prelucrare de care aveți nevoie să fie deja definită aici.
• Ca sugestie, exploatați cu încredere pattern matching, case și gărzi, în locul if-urilor imbricate.
• Pentru rularea testelor, încărcați în interpretor modulul TestGraph și evaluați checkAll.

• Schelet etapa 1
• Schelet etapa 2
• Schelet etapa 3

• Algebraic Graphs with Class (Functional Pearl)

• 04.05 (14:50) - Clarificare deadline hard
• 01.05 (19:40)
  • Etapa 2 - Flexibilizare testPartitions pentru a nu ține cont de ordinea elementelor și a submulțimilor.
  • Etapa 3 - Flexibilizare testMaximalModularPartition pentru a ține cont de ambele descompuneri valide de la ultimul subtest.
• 29.04 (11:35) - Etapa 3 - Publicare
• 19.04 (16:30) - Etapa 2 - Publicare
• 17.04 (18:54) - Etapa 1 - Actualizare checker, subtest 10 de la bfs, care apela dfs în loc de bfs.
• 17.04 (12:47) - Etapa 1 - Actualizare checker cu ordinea corectă a valorilor testate și corecte. În versiunea anterioară erau inversate, lucru ce ducea la mesaje confuze în cazul testelor picate.