Laboratorul 1 Proiectarea Logică
1. Sisteme de numeratie
Un număr N de forma cncn-1…c2c1c0 reprezentat în baza 10 are valoarea: N = cn*10n + cn-1*10n-1 +…+ c2*102 + c1*101 + c0*100
*ex: 12345 = 1*104 + 2*103 + 3*102 + 4*101 + 5*100
Baza unui sistem de numerație poate fi însă orice întreg b ≥ 2, ponderea cifrei din poziția i fiind în acest caz bi. În acest caz valoarea unui număr cncn-1…c2c1c0(b) reprezentat în baza b este: N = cn*bn + cn-1*bn-1 +…+ c2*b2 + c1*b1 + c0*b0 (1)
În circuitele digitale, semnalele pot avea, în mod normal, una din cele doua stări posibile. Aceste stări sunt asociate cifrelor binare 0 și 1, ceea ce face ca baza 2 să fie o alegere naturală pentru reprezentarea numerelor în sistemele digitale. *ex: 100101(2) = 1*25 + 0*24 + 0*23 + 1*22 + 0*21 + 1*20
O altă bază folosită în sistemele digitale este baza 16, deoarece permite o reprezentare mai facilă a numerelor decât baza 2, dealtfel și conversia între baza 2 și baza 16 fiind foarte rapidă. Cifrele folosite în baza 16 sunt, în ordinea crescătoare a valorii, 0..9 plus literele A, B, C, D, E și F.
*ex: 1EE7(16) = 1*163 + 14*162 + 14*161 + 7*160 = 7911(10)
Pentru a găsi reprezentarea unui număr într-o bază b este necesar să determinăm cifrele cncn-1…c2c1c0 care satisfac ecuația (1), ținând cont de faptul că ci < b. Rearanjând ecuația (1) obținem: N = (cn*bn-1 + cn-1*bn-2 +…+ c2*b1 + c1*b0)*b + c0
Se observă că tot ce trebuie să facem pentru a îl afla pe c0 este să împărțim numărul de convertit la b, c0 fiind chiar restul împărțirii. Câtul rezultat va fi apoi împarțit din nou la b pentru a afla pe c1 s.a.m.d. pentru celelate cifre c2,…,cn.
*ex: 37(10) = 100101(2)
| Cât | Rest | Cifra | |
|---|---|---|---|
| 37/2 | 18 | 1 | c0 |
| 18/2 | 9 | 0 | c1 |
| 9/2 | 4 | 1 | c2 |
| 4/2 | 2 | 0 | c3 |
| 2/2 | 1 | 0 | c4 |
| 1/2 | 0 | 1 | c5 |
*ex: 7911(10) = 1EE7(16)
| Cât | Rest | Cifra | |
|---|---|---|---|
| 7911/16 | 494 | 7 | c0 |
| 494/16 | 30 | 14 | c1 |
| 30/16 | 1 | 14 | c2 |
| 1/16 | 0 | 1 | c3 |
În cazul în care între baza sursă bs și baza destinație bd există o relație de forma bs=bdr sau bd=bsr conversia între cele doua baze se poate face mult mai ușor având în vedere că fiecare cifră a bazei mai mari poate fi scrisă ca un grup de r cifre ale bazei mai mici. *ex1: 16 = 24 *ex2: 1EE7(16)=0001111011100111(2) *ex3: 100101(2)=25(16)
2. Algebra booleană
Algebra booleană este o algebră formată din: * elementele 0 și 1 * 2 operații binare: ȘI (AND) și SAU (OR), notate simbolic cu (&, ∧ sau ∙), respectiv (|, ∨ sau +)
Operațiile sunt definite astfel:
<tabcaption legi center | Operații binare>
| NU | ȘI | SAU |
|---|---|---|
| !0 = 1 !1 = 0 | 0 & 0 = 0 0 & 1 = 0 1 & 0 = 0 1 & 1 = 1 | 0|0 = 0 0|1 = 1 1|0 = 1 1|1 = 1 |
</tabcaption>
Din aceste definiții rezultă o serie de teoreme ale algebrei booleene dintre care amintim câteva mai uzuale:
* Principiul dublei negații:
!(!x) = x
* Legile lui De Morgan:
!(x & y) = !x | !y
!(x | y) = !x & !y
* Elemente neutre:
x & 1 = 1 & x = x
x | 0 = 0 | x = x
===== 4. Reprezentarea funcțiilor logice =====
Pe lângă expresia booleană (coloana 2) sau schema porților logice (coloana 3) o funcție booleană mai poate fi descrisă și prin tabelul ei de adevăr. Această reprezentare poate fi observată în ultima coloană a tabelului anterior. Tabelul de adevăr al unei funcții cu n parametri conține n+1 coloane și, în general, 2n rânduri. Pentru fiecare rând, primele n coloane conțin câte o combinație de 0 și 1 pentru parametrii funcției, iar ultima coloană conține valoarea funcției pentru acea combinație a parametrilor. În anumite cazuri, tabelul de adevăr al unei funcții poate conține și x. Dacă simbolul x se găsește în coloanele parametrilor, înseamnă că, pentru acea combinație a parametrilor funcției, parametrul respectiv nu afectează ieșirea funcției. În alte cuvinte parametrul poate avea atât valoare 0 cât și valoarea 1, iar notația x este o prescurtare pentru această situație. Dacă simbolul x se găsește în coloana rezultatului, înseamnă că respectiva combinație de paramterii a funcției este invalidă, iar în acest caz rezultatul funcției nu este definit, el putând avea oricare dintre valorile 0 sau 1, depinzând de implementarea funcției.
Pornind de la expresia booleană sau schema logică a unei funcții tabelul de adevăr se poate determina calculând valoarea funcției pentru fiecare combinație a parametrilor ei. În sens invers, pornind de la tabelul de adevăr, o expresie booleană a funcției poate fi determinată luând fiecare rând al tabelului pentru care funcția are valoarea 1 și formând termeni compuși din parametrii negați și direcți ai funcției legați prin ȘI. Parametrul se ia în forma directă dacă pe rândul considerat el are valoare 1 și în forma negată daca are valoare 0. Toți termenii corespunzători rândurilor unde funcția are valoarea 1 sunt apoi legați prin SAU. Această formă a unei funcții mai este numită și forma normal disjunctivă. A se observa că, în general, expresia astfel obținută nu este minimă, în sensul că ea conține mai multe operații decât sunt necesare pentru a descrie funcția. Pornind de la această formulă se pot aplica diferite metode de minimizare a ei: grafică (folosind digrame Karnaugh) sau algebrică (folosind teoremele algebrei booleene).
Exemplu:
<tabcaption functie center|>
^ x ^ y ^ z ^ f ^
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
</tabcaption>
f(x,y,z) = (!x & !y & !z) | (!x & y & z) | (x & !y & !z) | (x & y & !z)
===== 5. Circuite Logice Combinaționale =====
Circuitele logice combinaționale sunt circuitele reprezentate prin porți logice ce aplică o funcție pe intrări. Valorile de ieșire depind doar de valorile de intrare, nu și de stări de reactie(feedback), iar cand starea unei intrări se schimbă, se reflectă imediat pe ieșiri.
<imgcaption image1 center | Diagrama bloc pentru un circuit combinațional cu n intrări și m ieșiri> </imgcaption>
Un circuit combinațional poate fi descris prin schema cu interconectarea porților, prin funcția(expresia) în logica booleană ce este aplicată pe intrări și prin tabele de adevăr (dacă nu au un număr prea mare de intrări).
Circuitele combinaționale sunt folosite în procesoare în cadrul componente de calcul, iar cele mai des întalnite sunt:
* multiplexoare și demultiplexoare
* codificatoare și decodificatoare
* sumatoare
* comparatoare
* memorii ROM (Read-Only Memory)
* memorii SRAM (Static Random Access Memory)
De exemplu folosim sumatoare în cadrul Unităților Aritmetice-Logice(UAL) sau bistabile pentru implementarea memoriei cache din interiorul unui procesor.
<note important>Pentru simularea circuitelor logice din acest laborator vom folosi simulatorul online Falstad. Acesta este un applet Java care poate fi rulat direct din browser și permite proiectarea de circuite logice combinaționale și secvențiale, precum și vizualizarea facilă a stărilor intrărilor și ieșirilor din circuit. Puteți rula simulatorul de aici. </note>
==== 5.1 Porți logice ====
Porțile logice se folosesc în circuitele digitale pentru a implementa operațiile din algebra booleană.
În tabelul următor sunt prezentate cele mai întâlnite porți logice împreună cu funcția booleană pe care o implementează:
<tabcaption porti center | Porțile logice de bază>
^ Denumire ^ Simbol ^ Operator ^ Tabel de adevăr ^^^
| Inversor (NOT) |
</imgcaption>
Un circuit combinațional poate fi descris prin schema cu interconectarea porților, prin funcția(expresia) în logica booleană ce este aplicată pe intrări și prin tabele de adevăr (dacă nu au un număr prea mare de intrări).
Circuitele combinaționale sunt folosite în procesoare în cadrul componente de calcul, iar cele mai des întalnite sunt:
* multiplexoare și demultiplexoare
* codificatoare și decodificatoare
* sumatoare
* comparatoare
* memorii ROM (Read-Only Memory)
* memorii SRAM (Static Random Access Memory)
De exemplu folosim sumatoare în cadrul Unităților Aritmetice-Logice(UAL) sau bistabile pentru implementarea memoriei cache din interiorul unui procesor.
<note important>Pentru simularea circuitelor logice din acest laborator vom folosi simulatorul online Falstad. Acesta este un applet Java care poate fi rulat direct din browser și permite proiectarea de circuite logice combinaționale și secvențiale, precum și vizualizarea facilă a stărilor intrărilor și ieșirilor din circuit. Puteți rula simulatorul de aici. </note>
==== 5.1 Porți logice ====
Porțile logice se folosesc în circuitele digitale pentru a implementa operațiile din algebra booleană.
În tabelul următor sunt prezentate cele mai întâlnite porți logice împreună cu funcția booleană pe care o implementează:
<tabcaption porti center | Porțile logice de bază>
^ Denumire ^ Simbol ^ Operator ^ Tabel de adevăr ^^^
| Inversor (NOT) |  | f = !a | a || f |
| ::: | ::: | ::: | 0 || 1 |
| ::: | ::: | ::: | 1 || 0 |
| Poarta SAU
| f = !a | a || f |
| ::: | ::: | ::: | 0 || 1 |
| ::: | ::: | ::: | 1 || 0 |
| Poarta SAU
(OR) | 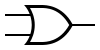 | f = a || b | a | b | f |
| ::: | ::: | ::: | 0 | 0 | 0 |
| ::: | ::: | ::: | 0 | 1 | 1 |
| ::: | ::: | ::: | 1 | 0 | 1 |
| ::: | ::: | ::: | 1 | 1 | 1 |
| Poarta ŞI
| f = a || b | a | b | f |
| ::: | ::: | ::: | 0 | 0 | 0 |
| ::: | ::: | ::: | 0 | 1 | 1 |
| ::: | ::: | ::: | 1 | 0 | 1 |
| ::: | ::: | ::: | 1 | 1 | 1 |
| Poarta ŞI
(AND) | 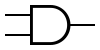 | f = a && b | a | b | f |
| ::: | ::: | ::: | 0 | 0 | 0 |
| ::: | ::: | ::: | 0 | 1 | 0 |
| ::: | ::: | ::: | 1 | 0 | 0 |
| ::: | ::: | ::: | 1 | 1 | 1 |
| Poarta
| f = a && b | a | b | f |
| ::: | ::: | ::: | 0 | 0 | 0 |
| ::: | ::: | ::: | 0 | 1 | 0 |
| ::: | ::: | ::: | 1 | 0 | 0 |
| ::: | ::: | ::: | 1 | 1 | 1 |
| Poarta
SAU-NU
(NOR) | 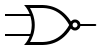 | f = !(a || b) | a | b | f |
| ::: | ::: | ::: | 0 | 0 | 1 |
| ::: | ::: | ::: | 0 | 1 | 0 |
| ::: | ::: | ::: | 1 | 0 | 0 |
| ::: | ::: | ::: | 1 | 1 | 0 |
| Poarta
| f = !(a || b) | a | b | f |
| ::: | ::: | ::: | 0 | 0 | 1 |
| ::: | ::: | ::: | 0 | 1 | 0 |
| ::: | ::: | ::: | 1 | 0 | 0 |
| ::: | ::: | ::: | 1 | 1 | 0 |
| Poarta
ŞI-NU
(NAND) |  | f = !(a && b) | a | b | f |
| ::: | ::: | ::: | 0 | 0 | 1 |
| ::: | ::: | ::: | 0 | 1 | 1 |
| ::: | ::: | ::: | 1 | 0 | 1 |
| ::: | ::: | ::: | 1 | 1 | 0 |
| Poarta
| f = !(a && b) | a | b | f |
| ::: | ::: | ::: | 0 | 0 | 1 |
| ::: | ::: | ::: | 0 | 1 | 1 |
| ::: | ::: | ::: | 1 | 0 | 1 |
| ::: | ::: | ::: | 1 | 1 | 0 |
| Poarta
SAU EXCLUSIV
(XOR) | 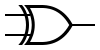 | f = a ^ b | a | b | f |
| ::: | ::: | ::: | 0 | 0 | 0 |
| ::: | ::: | ::: | 0 | 1 | 1 |
| ::: | ::: | ::: | 1 | 0 | 1 |
| ::: | ::: | ::: | 1 | 1 | 0 |
| Poarta
| f = a ^ b | a | b | f |
| ::: | ::: | ::: | 0 | 0 | 0 |
| ::: | ::: | ::: | 0 | 1 | 1 |
| ::: | ::: | ::: | 1 | 0 | 1 |
| ::: | ::: | ::: | 1 | 1 | 0 |
| Poarta
SAU EXCLUSIV NU
(XNOR) |  | f = !(a ^ b) | a | b | f |
| ::: | ::: | ::: | 0 | 0 | 1 |
| ::: | ::: | ::: | 0 | 1 | 0 |
| ::: | ::: | ::: | 1 | 0 | 0 |
| ::: | ::: | ::: | 1 | 1 | 1 |
</tabcaption>
<note>
Rulați codul de mai jos (secțiunea hidden) în simulatorul Falstad: Copy la cod → În fereastra de Falstad File>Import apoi Paste și apăsați butonul Import.
Rulați și observați funcționarea fiecărui tip de poartă logică.
</note>
<note>
Realizați conexiunile pentru fiecare tip de poartă logică de pe suportul de laborator și testați funcționarea lor.
</note>
<hidden (Click aici) Codul pentru simulatorul Falstad pentru porțile logice >
<code>
$ 1 5.0E-6 10.20027730826997 50 5.0 50
150 480 144 608 144 0 2 0.0
152 480 240 608 240 0 2 0.0
151 480 336 608 336 0 2 5.0
153 480 432 608 432 0 2 5.0
I 480 48 608 48 0 0.5
L 480 48 400 48 0 0 false 5.0 0.0
L 480 128 400 128 0 0 false 5.0 0.0
L 480 160 400 160 0 0 false 5.0 0.0
L 480 224 400 224 0 0 false 5.0 0.0
L 480 256 400 256 0 0 false 5.0 0.0
L 480 320 400 320 0 0 false 5.0 0.0
L 480 352 400 352 0 0 false 5.0 0.0
L 480 416 400 416 0 0 false 5.0 0.0
L 480 448 400 448 0 0 false 5.0 0.0
M 608 48 688 48 0 2.5
M 608 144 688 144 0 2.5
M 608 240 688 240 0 2.5
M 608 336 688 336 0 2.5
M 608 432 688 432 0 2.5
x 520 103 569 109 0 24 AND
x 516 206 552 212 0 24 OR
x 517 301 583 307 0 24 NAND
x 517 398 570 404 0 24 NOR
x 520 17 570 23 0 24 NOT
154 480 512 608 512 0 2 0.0
L 480 496 400 496 0 0 false 5.0 0.0
L 480 528 400 528 0 0 false 5.0 0.0
M 608 512 688 512 0 2.5
x 515 480 566 486 0 24 XOR
</code>
</hidden>
| f = !(a ^ b) | a | b | f |
| ::: | ::: | ::: | 0 | 0 | 1 |
| ::: | ::: | ::: | 0 | 1 | 0 |
| ::: | ::: | ::: | 1 | 0 | 0 |
| ::: | ::: | ::: | 1 | 1 | 1 |
</tabcaption>
<note>
Rulați codul de mai jos (secțiunea hidden) în simulatorul Falstad: Copy la cod → În fereastra de Falstad File>Import apoi Paste și apăsați butonul Import.
Rulați și observați funcționarea fiecărui tip de poartă logică.
</note>
<note>
Realizați conexiunile pentru fiecare tip de poartă logică de pe suportul de laborator și testați funcționarea lor.
</note>
<hidden (Click aici) Codul pentru simulatorul Falstad pentru porțile logice >
<code>
$ 1 5.0E-6 10.20027730826997 50 5.0 50
150 480 144 608 144 0 2 0.0
152 480 240 608 240 0 2 0.0
151 480 336 608 336 0 2 5.0
153 480 432 608 432 0 2 5.0
I 480 48 608 48 0 0.5
L 480 48 400 48 0 0 false 5.0 0.0
L 480 128 400 128 0 0 false 5.0 0.0
L 480 160 400 160 0 0 false 5.0 0.0
L 480 224 400 224 0 0 false 5.0 0.0
L 480 256 400 256 0 0 false 5.0 0.0
L 480 320 400 320 0 0 false 5.0 0.0
L 480 352 400 352 0 0 false 5.0 0.0
L 480 416 400 416 0 0 false 5.0 0.0
L 480 448 400 448 0 0 false 5.0 0.0
M 608 48 688 48 0 2.5
M 608 144 688 144 0 2.5
M 608 240 688 240 0 2.5
M 608 336 688 336 0 2.5
M 608 432 688 432 0 2.5
x 520 103 569 109 0 24 AND
x 516 206 552 212 0 24 OR
x 517 301 583 307 0 24 NAND
x 517 398 570 404 0 24 NOR
x 520 17 570 23 0 24 NOT
154 480 512 608 512 0 2 0.0
L 480 496 400 496 0 0 false 5.0 0.0
L 480 528 400 528 0 0 false 5.0 0.0
M 608 512 688 512 0 2.5
x 515 480 566 486 0 24 XOR
</code>
</hidden>
=== Realizarea funcției XOR folosind logică NAND ===
<imgcaption image7 center | Poartă XOR realizată cu patru porți NAND> </imgcaption>
<note>
Rulați codul de mai jos (secțiunea hidden) în simulatorul Falstad: Copy la cod → În fereastra de Falstad File>Import apoi Paste și apăsați butonul Import.
Rulați și observați funcționarea circuitului. Determinați dacă este echivalent cu o poartă XOR.
</note>
<note>
Construiți circuitul porții XOR cu logică NAND pe suportul de laborator și testați funcționarea corectă.
</note>
<hidden (Click aici) Codul pentru simulatorul Falstad pentru poarta XOR cu logică NAND >
<code>
$ 1 5.0E-6 10.20027730826997 50 5.0 50
151 496 224 624 224 0 2 5.0
151 496 320 624 320 0 2 5.0
151 656 272 768 272 0 2 0.0
151 368 272 480 272 0 2 5.0
w 496 240 480 240 0
w 480 240 480 272 0
w 480 272 480 304 0
w 480 304 496 304 0
w 496 208 368 208 0
w 368 208 368 256 0
w 368 288 368 336 0
w 496 336 368 336 0
w 368 208 288 208 0
w 368 336 288 336 0
w 624 224 624 256 0
w 624 320 624 288 0
w 656 288 624 288 0
w 656 256 624 256 0
M 768 272 848 272 0 2.5
L 288 208 224 208 0 0 false 5.0 0.0
L 288 336 224 336 0 0 false 5.0 0.0
</code>
</hidden>
</imgcaption>
<note>
Rulați codul de mai jos (secțiunea hidden) în simulatorul Falstad: Copy la cod → În fereastra de Falstad File>Import apoi Paste și apăsați butonul Import.
Rulați și observați funcționarea circuitului. Determinați dacă este echivalent cu o poartă XOR.
</note>
<note>
Construiți circuitul porții XOR cu logică NAND pe suportul de laborator și testați funcționarea corectă.
</note>
<hidden (Click aici) Codul pentru simulatorul Falstad pentru poarta XOR cu logică NAND >
<code>
$ 1 5.0E-6 10.20027730826997 50 5.0 50
151 496 224 624 224 0 2 5.0
151 496 320 624 320 0 2 5.0
151 656 272 768 272 0 2 0.0
151 368 272 480 272 0 2 5.0
w 496 240 480 240 0
w 480 240 480 272 0
w 480 272 480 304 0
w 480 304 496 304 0
w 496 208 368 208 0
w 368 208 368 256 0
w 368 288 368 336 0
w 496 336 368 336 0
w 368 208 288 208 0
w 368 336 288 336 0
w 624 224 624 256 0
w 624 320 624 288 0
w 656 288 624 288 0
w 656 256 624 256 0
M 768 272 848 272 0 2.5
L 288 208 224 208 0 0 false 5.0 0.0
L 288 336 224 336 0 0 false 5.0 0.0
</code>
</hidden>
=== Realizarea funcției XOR folosind logică NOR ===
<imgcaption image8 center | Poartă XOR realizată cu patru porți NOR>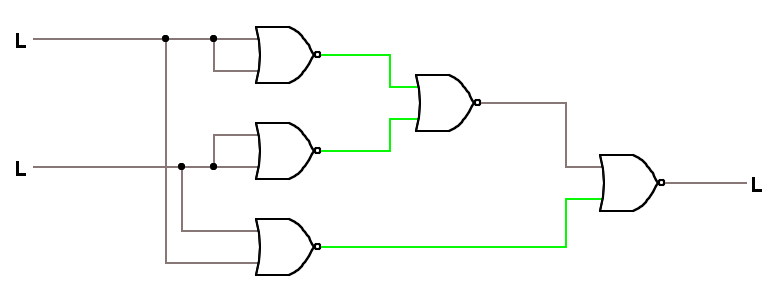 </imgcaption>
<note>
Rulați codul de mai jos (secțiunea hidden) în simulatorul Falstad: Copy la cod → În fereastra de Falstad File>Import apoi Paste și apăsați butonul Import.
Rulați și observați funcționarea circuitului. Determinați dacă este echivalent cu o poartă XOR.
</note>
<note>
Construiți circuitul porții XOR cu logică NOR pe suportul de laborator și testați funcționarea corectă.
</note>
<hidden (Click aici) Codul pentru simulatorul Falstad pentru poarta XOR cu logică NOR >
<code>
$ 1 5.0E-6 10.20027730826997 50 5.0 50
153 304 176 448 176 0 2 5.0
153 304 272 448 272 0 2 5.0
153 304 368 448 368 0 2 5.0
153 480 224 592 224 0 2 0.0
153 656 304 784 304 0 2 0.0
w 592 224 656 224 0
w 656 288 656 224 0
w 448 176 480 176 0
w 480 176 480 208 0
w 448 272 480 272 0
w 480 240 480 272 0
w 448 368 656 368 0
w 656 320 656 368 0
w 304 160 304 192 0
w 304 256 304 288 0
w 304 352 272 352 0
w 304 288 272 288 0
w 272 288 272 352 0
w 304 384 256 384 0
w 304 160 256 160 0
w 256 160 256 384 0
w 256 160 176 160 0
w 272 288 176 288 0
L 176 160 112 160 0 0 false 5.0 0.0
L 176 288 112 288 0 0 false 5.0 0.0
M 784 304 848 304 0 2.5
</code>
</hidden>
</imgcaption>
<note>
Rulați codul de mai jos (secțiunea hidden) în simulatorul Falstad: Copy la cod → În fereastra de Falstad File>Import apoi Paste și apăsați butonul Import.
Rulați și observați funcționarea circuitului. Determinați dacă este echivalent cu o poartă XOR.
</note>
<note>
Construiți circuitul porții XOR cu logică NOR pe suportul de laborator și testați funcționarea corectă.
</note>
<hidden (Click aici) Codul pentru simulatorul Falstad pentru poarta XOR cu logică NOR >
<code>
$ 1 5.0E-6 10.20027730826997 50 5.0 50
153 304 176 448 176 0 2 5.0
153 304 272 448 272 0 2 5.0
153 304 368 448 368 0 2 5.0
153 480 224 592 224 0 2 0.0
153 656 304 784 304 0 2 0.0
w 592 224 656 224 0
w 656 288 656 224 0
w 448 176 480 176 0
w 480 176 480 208 0
w 448 272 480 272 0
w 480 240 480 272 0
w 448 368 656 368 0
w 656 320 656 368 0
w 304 160 304 192 0
w 304 256 304 288 0
w 304 352 272 352 0
w 304 288 272 288 0
w 272 288 272 352 0
w 304 384 256 384 0
w 304 160 256 160 0
w 256 160 256 384 0
w 256 160 176 160 0
w 272 288 176 288 0
L 176 160 112 160 0 0 false 5.0 0.0
L 176 288 112 288 0 0 false 5.0 0.0
M 784 304 848 304 0 2.5
</code>
</hidden>
==== 5.2 Comparatoare ====
Comparatoarele digitale sunt circuite combinaționale care primesc la intrare două numere reprezentate în formă binară și determină dacă unul dintre numere este mai mare, mai mic sau egal cu al doilea număr. Circuitele de tip comparator sunt folosite în microprocesoare sau în microcontrollere.
<imgcaption image5 center | Diagrama bloc pentru un comparator de două numere pe N biți>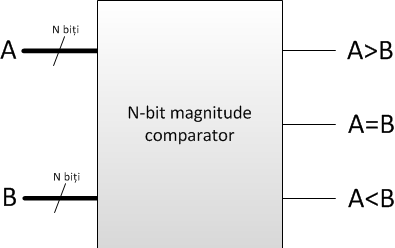 </imgcaption>
<note tip>O poartă SAU EXCLUSIV NU (XNOR) este un comparator de egalitate pentru două numere de un singur bit, deoarece ieșirea acesteia este ”1” dacă și numai dacă cele două intrări au aceeași stare logică.</note>
Operarea unui comparator cu intrări pe doi biți poate fi exprimată folosind tabela de adevăr de mai jos:
<tabcaption comparator center| Tabela de adevăr pentru un comparator pe doi biți>
^Intrări^^^^Ieșiri^^^
^ A1 ^ A0 ^ B1 ^ B0 ^ A<B ^ A=B ^ A>B ^
| 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 1 | 0 |
</tabcaption>
Pornind de la tabelul de mai sus putem obține expresiile booleene pentru fiecare din funcțiile de mai sus (A>B, A=B și A<B) prin minimizarea cu tabele Karnaugh.
<tabcaption comp1 center>
^ A>B ^^^^^
^ B1B0/A1A0 ^ 00 ^ 01 ^ 10 ^ 11 ^
^ 00 | | | | |
^ 01 | 1 | | | |
^ 10 | 1 | 1 | | 1 |
^ 11 | 1 | 1 | | |
</tabcaption>
<tabcaption comp2 center>
^ A=B ^^^^^
^ B1B0/A1A0 ^ 00 ^ 01 ^ 10 ^ 11 ^
^ 00 | 1 | | | |
^ 01 | | 1 | | |
^ 10 | | | 1 | |
^ 11 | | | | 1 |
</tabcaption>
<tabcaption comp3 center>
^ A<B ^^^^^
^ B1B0/A1A0 ^ 00 ^ 01 ^ 10 ^ 11 ^
^ 00 | | 1 | 1 | 1 |
^ 01 | | | 1 | 1 |
^ 10 | | | | |
^ 11 | | | 1 | |
</tabcaption>
—-
După minimizare, obținem următoarele expresii:
<latex>
\begin{alltt}
\mathbf{A>B:}\\A_1\cdot \overline{B_1}+A_0\cdot\overline{B_0}\cdot\overline{A_1}\cdot\overline{B_1}+A_0\cdot\overline{B_0}\cdot A_1 \cdot B_1 =
</imgcaption>
<note tip>O poartă SAU EXCLUSIV NU (XNOR) este un comparator de egalitate pentru două numere de un singur bit, deoarece ieșirea acesteia este ”1” dacă și numai dacă cele două intrări au aceeași stare logică.</note>
Operarea unui comparator cu intrări pe doi biți poate fi exprimată folosind tabela de adevăr de mai jos:
<tabcaption comparator center| Tabela de adevăr pentru un comparator pe doi biți>
^Intrări^^^^Ieșiri^^^
^ A1 ^ A0 ^ B1 ^ B0 ^ A<B ^ A=B ^ A>B ^
| 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 1 | 0 |
</tabcaption>
Pornind de la tabelul de mai sus putem obține expresiile booleene pentru fiecare din funcțiile de mai sus (A>B, A=B și A<B) prin minimizarea cu tabele Karnaugh.
<tabcaption comp1 center>
^ A>B ^^^^^
^ B1B0/A1A0 ^ 00 ^ 01 ^ 10 ^ 11 ^
^ 00 | | | | |
^ 01 | 1 | | | |
^ 10 | 1 | 1 | | 1 |
^ 11 | 1 | 1 | | |
</tabcaption>
<tabcaption comp2 center>
^ A=B ^^^^^
^ B1B0/A1A0 ^ 00 ^ 01 ^ 10 ^ 11 ^
^ 00 | 1 | | | |
^ 01 | | 1 | | |
^ 10 | | | 1 | |
^ 11 | | | | 1 |
</tabcaption>
<tabcaption comp3 center>
^ A<B ^^^^^
^ B1B0/A1A0 ^ 00 ^ 01 ^ 10 ^ 11 ^
^ 00 | | 1 | 1 | 1 |
^ 01 | | | 1 | 1 |
^ 10 | | | | |
^ 11 | | | 1 | |
</tabcaption>
—-
După minimizare, obținem următoarele expresii:
<latex>
\begin{alltt}
\mathbf{A>B:}\\A_1\cdot \overline{B_1}+A_0\cdot\overline{B_0}\cdot\overline{A_1}\cdot\overline{B_1}+A_0\cdot\overline{B_0}\cdot A_1 \cdot B_1 =
A_1 \cdot \overline{B_1}+A_0 \cdot \overline{B_0} \cdot (\overline{A_1} \cdot \overline{B_1}+A_1\cdot B_1)=\\A_1 \cdot \overline{B_1}+A_0 \cdot \overline{B_0} \cdot X_1
\end{alltt}
</latex>
<latex>
\begin{alltt}
\mathbf{A=B:}
\overline{A_1}\cdot\overline{A_0}\cdot\overline{B_1}\cdot\overline{B_0}+A_0\cdot B_0\cdot\overline{A_1}\cdot\overline{B_1}+\overline{A_0}\cdot\overline{B_0}\cdot A_1\cdot B_1+A_1\cdot A_0\cdot B_1\cdot B_0=
\end{alltt}
</latex>
<latex>
(\overline{A_1} \cdot \overline{B_1}+A_1 \cdot B_1 ) (\overline{A_0} \cdot \overline{B_0}+A_0 \cdot B_0 )=\\X_1 \cdot X_0
</latex>
<latex>
\mathbf{A<B:}
\overline{A_1}\cdot B_1+\overline{A_0}\cdot B_0\cdot\overline{A_1}\cdot\overline{B_1}+\overline{A_0}\cdot B_0 \cdot A_1 \cdot B_1 =
\overline{A_1}\cdot B_1+\overline{A_0}\cdot B_0\cdot X_1
</latex>
Pornind de la această minimizare, putem proiecta schema logică a comparatorului, ca în figura de mai jos.
<imgcaption image6 center | Schema logică a comparatorului>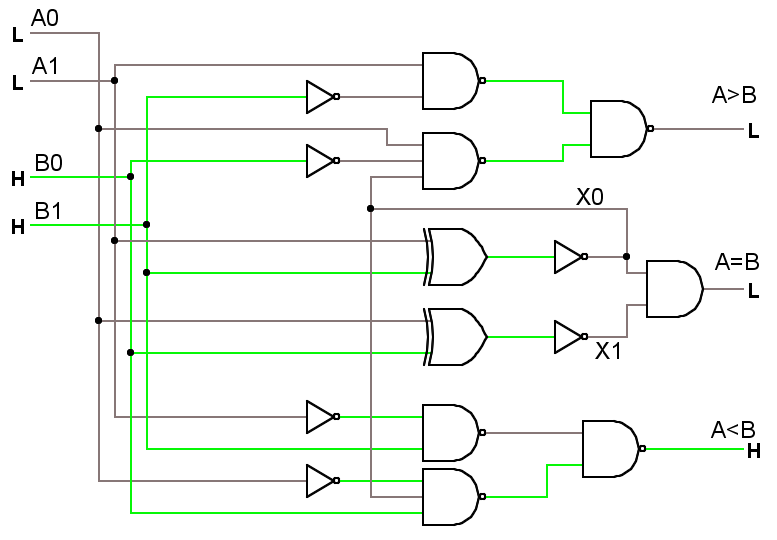 </imgcaption>
<hidden (Click aici) Codul pentru simulatorul Falstad pentru comparatorul pe doi biți >
<code>
$ 1 5.0E-6 10.20027730826997 50 5.0 50
151 528 80 656 80 0 2 5.0
151 528 160 656 160 0 3 5.0
151 704 128 816 128 0 2 0.0
w 656 80 704 80 0
w 704 80 704 112 0
w 656 160 704 160 0
w 704 144 704 160 0
M 816 128 896 128 0 2.5
x 854 103 899 109 0 24 A>B
154 528 256 672 256 0 2 5.0
154 528 336 672 336 0 2 5.0
I 672 256 752 256 0 0.5
I 672 336 752 336 0 0.5
150 768 288 864 288 0 2 0.0
w 752 256 768 256 0
w 768 256 768 272 0
w 768 304 768 336 0
w 752 336 768 336 0
M 864 288 896 288 0 2.5
151 528 432 656 432 0 2 0.0
151 528 496 656 496 0 3 5.0
151 688 448 816 448 0 2 5.0
w 656 432 688 432 0
w 688 464 688 496 0
w 656 496 688 496 0
M 816 448 896 448 0 2.5
w 768 256 768 208 0
I 400 416 528 416 0 0.5
I 400 480 528 480 0 0.5
w 528 512 512 512 0
w 512 208 768 208 0
w 528 176 512 176 0
w 512 176 512 208 0
I 400 160 528 160 0 0.5
I 400 96 528 96 0 0.5
x 718 205 746 211 0 24 X0
x 737 359 765 365 0 24 X1
x 857 270 902 276 0 24 A=B
x 853 438 898 444 0 24 A<B
L 224 32 160 32 0 0 false 5.0 0.0
L 224 80 160 80 0 0 false 5.0 0.0
w 528 144 528 128 0
w 528 128 240 128 0
w 240 128 240 32 0
w 240 32 224 32 0
w 528 320 240 320 0
w 240 128 240 320 0
w 400 480 240 480 0
w 240 320 240 480 0
w 528 64 256 64 0
w 256 64 256 80 0
w 256 80 224 80 0
w 400 416 256 416 0
x 173 26 201 32 0 24 A0
x 174 74 202 80 0 24 A1
L 224 176 160 176 0 1 false 5.0 0.0
L 224 224 160 224 0 1 false 5.0 0.0
w 528 352 272 352 0
w 272 176 224 176 0
w 272 176 272 352 0
w 400 160 272 160 0
w 272 160 272 176 0
w 272 352 272 496 0
w 400 96 304 96 0
w 288 224 224 224 0
w 288 224 288 96 0
w 304 96 288 96 0
w 528 272 288 272 0
w 288 224 288 272 0
w 528 240 256 240 0
w 256 80 256 240 0
w 256 240 256 416 0
w 528 448 288 448 0
w 288 272 288 448 0
x 176 171 205 177 0 24 B0
x 176 219 205 225 0 24 B1
w 528 496 512 496 0
w 512 496 512 208 0
w 512 512 272 512 0
w 272 496 272 512 0
</code>
</hidden>
<note>
Rulați codul de mai sus în simulatorul Falstad: Copy la cod → În fereastra de Falstad File>Import apoi Paste și apăsați butonul Import.
Rulați și observați funcționarea.
</note>
<note>
Pornind de la exemplul de rulare și minimizările de mai sus, modificați circuitul comparatorului pentru a folosi numai porți de tip NOT, NAND și NOR.
</note>
==== 5.3 Sumatoare ====
Sumatoarele (adders), folosite cel mai mult în unitățile aritmetice logice ale procesoarelor, realizează adunări pe un număr dat de biți, furnizând la ieșirea circuitului suma și transportul (carry) rezultat în urma operației.
Există mai multe tipuri de sumatoare pentru adunarea numerelor pe n biți, iar acestea se bazează pe sumatoare simple de 1 bit, care pot fi de două tipuri:
* sumatorul elementar parțial (Half adder) - însumează doi operanzi pe 1 bit și oferă la ieșire suma acestora și transportul.
* sumatorul elementar complet (Full adder) - însumează doi operanzi pe 1 bit și un transport și oferă la ieșire suma acestora și transportul.
<imgcaption image2 | Diagrama bloc pentru half adder>
</imgcaption>
<hidden (Click aici) Codul pentru simulatorul Falstad pentru comparatorul pe doi biți >
<code>
$ 1 5.0E-6 10.20027730826997 50 5.0 50
151 528 80 656 80 0 2 5.0
151 528 160 656 160 0 3 5.0
151 704 128 816 128 0 2 0.0
w 656 80 704 80 0
w 704 80 704 112 0
w 656 160 704 160 0
w 704 144 704 160 0
M 816 128 896 128 0 2.5
x 854 103 899 109 0 24 A>B
154 528 256 672 256 0 2 5.0
154 528 336 672 336 0 2 5.0
I 672 256 752 256 0 0.5
I 672 336 752 336 0 0.5
150 768 288 864 288 0 2 0.0
w 752 256 768 256 0
w 768 256 768 272 0
w 768 304 768 336 0
w 752 336 768 336 0
M 864 288 896 288 0 2.5
151 528 432 656 432 0 2 0.0
151 528 496 656 496 0 3 5.0
151 688 448 816 448 0 2 5.0
w 656 432 688 432 0
w 688 464 688 496 0
w 656 496 688 496 0
M 816 448 896 448 0 2.5
w 768 256 768 208 0
I 400 416 528 416 0 0.5
I 400 480 528 480 0 0.5
w 528 512 512 512 0
w 512 208 768 208 0
w 528 176 512 176 0
w 512 176 512 208 0
I 400 160 528 160 0 0.5
I 400 96 528 96 0 0.5
x 718 205 746 211 0 24 X0
x 737 359 765 365 0 24 X1
x 857 270 902 276 0 24 A=B
x 853 438 898 444 0 24 A<B
L 224 32 160 32 0 0 false 5.0 0.0
L 224 80 160 80 0 0 false 5.0 0.0
w 528 144 528 128 0
w 528 128 240 128 0
w 240 128 240 32 0
w 240 32 224 32 0
w 528 320 240 320 0
w 240 128 240 320 0
w 400 480 240 480 0
w 240 320 240 480 0
w 528 64 256 64 0
w 256 64 256 80 0
w 256 80 224 80 0
w 400 416 256 416 0
x 173 26 201 32 0 24 A0
x 174 74 202 80 0 24 A1
L 224 176 160 176 0 1 false 5.0 0.0
L 224 224 160 224 0 1 false 5.0 0.0
w 528 352 272 352 0
w 272 176 224 176 0
w 272 176 272 352 0
w 400 160 272 160 0
w 272 160 272 176 0
w 272 352 272 496 0
w 400 96 304 96 0
w 288 224 224 224 0
w 288 224 288 96 0
w 304 96 288 96 0
w 528 272 288 272 0
w 288 224 288 272 0
w 528 240 256 240 0
w 256 80 256 240 0
w 256 240 256 416 0
w 528 448 288 448 0
w 288 272 288 448 0
x 176 171 205 177 0 24 B0
x 176 219 205 225 0 24 B1
w 528 496 512 496 0
w 512 496 512 208 0
w 512 512 272 512 0
w 272 496 272 512 0
</code>
</hidden>
<note>
Rulați codul de mai sus în simulatorul Falstad: Copy la cod → În fereastra de Falstad File>Import apoi Paste și apăsați butonul Import.
Rulați și observați funcționarea.
</note>
<note>
Pornind de la exemplul de rulare și minimizările de mai sus, modificați circuitul comparatorului pentru a folosi numai porți de tip NOT, NAND și NOR.
</note>
==== 5.3 Sumatoare ====
Sumatoarele (adders), folosite cel mai mult în unitățile aritmetice logice ale procesoarelor, realizează adunări pe un număr dat de biți, furnizând la ieșirea circuitului suma și transportul (carry) rezultat în urma operației.
Există mai multe tipuri de sumatoare pentru adunarea numerelor pe n biți, iar acestea se bazează pe sumatoare simple de 1 bit, care pot fi de două tipuri:
* sumatorul elementar parțial (Half adder) - însumează doi operanzi pe 1 bit și oferă la ieșire suma acestora și transportul.
* sumatorul elementar complet (Full adder) - însumează doi operanzi pe 1 bit și un transport și oferă la ieșire suma acestora și transportul.
<imgcaption image2 | Diagrama bloc pentru half adder> </imgcaption>
<imgcaption image3 | Diagrama bloc pentru full adder>
</imgcaption>
<imgcaption image3 | Diagrama bloc pentru full adder> </imgcaption>
==== Sumatorul elementar parțial ====
Acest sumator este în continuare descris prin expresiile boolene, tabelul de adevăr și schema logică.
<tabcaption table2 center | Tabelul de adevăr pentru half adder>
^ Inputs ^^ Outputs ^^
^ a ^ b ^ sum ^ cout ^
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
</tabcaption>
Din tabelul de adevăr se pot deduce următoarele formule:
<latex>
sum = a ⊕ b
</imgcaption>
==== Sumatorul elementar parțial ====
Acest sumator este în continuare descris prin expresiile boolene, tabelul de adevăr și schema logică.
<tabcaption table2 center | Tabelul de adevăr pentru half adder>
^ Inputs ^^ Outputs ^^
^ a ^ b ^ sum ^ cout ^
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
</tabcaption>
Din tabelul de adevăr se pot deduce următoarele formule:
<latex>
sum = a ⊕ b
c_{out} = a \cdot b
</latex>
Conform acestor formule putem exprima circuitul prin porți logice, ca în <imgref image4>:
<imgcaption image4 center | Schema logică pentru half adder>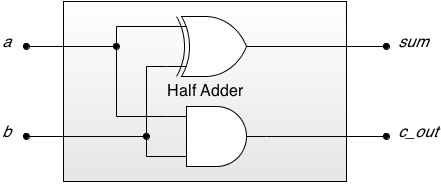 </imgcaption>
<hidden Despre tabele de adevăr și deducerea expresiilor boolene (click aici)>
Dintr-un tabel de adevăr, pentru fiecare output se va deduce o funcție/expresie aplicând următoarele reguli:
- se ia fiecare rând pentru care funcția are valoarea 1, care va forma un termen
- termenii sunt formați din parametrii funcției legați prin ȘI
- dacă parametrul are valoarea 1 se consideră în formă directă
- dacă parametrul are valoarea 0 se consideră în formă negată
- se aplică SAU între toți termenii deduși
Pentru sumatorului elementar parțial avem:
<latex> sum\ =\ \bar a\ \cdotp\ b\ +\ a\ \cdotp\ \bar b </latex>
<latex> c_{out}\ =\ a\ \cdotp \ b </latex>
În multe cazuri aceste formule sunt prea complexe, conținând multe operații și necesitând multe porți logice pentru a fi implementate. Pentru a reduce complexitatea formulelor rezultate se poate aplica un procedeu de minimizare**. Minimizarea se poate realiza folosind teoremele algebrei boolene, prin reducerea dimensiunii termenilor sau chiar eliminarea lor, sau grafic, prin diagrame Karnaugh.
</imgcaption>
<hidden Despre tabele de adevăr și deducerea expresiilor boolene (click aici)>
Dintr-un tabel de adevăr, pentru fiecare output se va deduce o funcție/expresie aplicând următoarele reguli:
- se ia fiecare rând pentru care funcția are valoarea 1, care va forma un termen
- termenii sunt formați din parametrii funcției legați prin ȘI
- dacă parametrul are valoarea 1 se consideră în formă directă
- dacă parametrul are valoarea 0 se consideră în formă negată
- se aplică SAU între toți termenii deduși
Pentru sumatorului elementar parțial avem:
<latex> sum\ =\ \bar a\ \cdotp\ b\ +\ a\ \cdotp\ \bar b </latex>
<latex> c_{out}\ =\ a\ \cdotp \ b </latex>
În multe cazuri aceste formule sunt prea complexe, conținând multe operații și necesitând multe porți logice pentru a fi implementate. Pentru a reduce complexitatea formulelor rezultate se poate aplica un procedeu de minimizare**. Minimizarea se poate realiza folosind teoremele algebrei boolene, prin reducerea dimensiunii termenilor sau chiar eliminarea lor, sau grafic, prin diagrame Karnaugh.
</hidden>
Rulați codul de mai jos (secțiunea hidden) în simulatorul Falstad: Copy la cod → În fereastra de Falstad File>Import apoi Paste și apăsați butonul Import. Rulați și observați funcționarea sumatorului fără carry.
<hidden (Click aici) Codul pentru simulatorul Falstad pentru sumatorul fără carry >
$ 1 5.0E-6 1.500424758475255 50 5.0 50 154 512 320 656 320 0 2 0.0 150 512 224 656 224 0 2 0.0 L 416 240 368 240 2 0 false 5.0 0.0 L 416 304 368 304 2 0 false 5.0 0.0 w 416 304 448 304 0 w 448 304 448 208 0 w 448 208 512 208 0 w 448 304 512 304 0 w 416 240 480 240 0 w 480 240 480 336 0 w 480 336 512 336 0 w 480 240 512 240 0 M 656 224 704 224 2 2.5 M 656 320 704 320 2 2.5 x 643 306 689 312 0 24 sum x 642 213 706 219 0 24 C_out x 375 229 388 235 0 24 a x 376 294 390 300 0 24 b
</hidden>
Sumatorul elementar complet
<tabcaption table3 center | Tabelul de adevăr pentru full adder>
| Inputs | Outputs | |||
|---|---|---|---|---|
| a | b | cin | sum | cout |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
</tabcaption>
Din tabelul de adevăr se pot deduce următoarele formule:

Conform acestor formule putem exprima circuitul prin porți logice sau putem folosi sumatoare elementare parțiale, ca în <imgref image5>:
<imgcaption image5 center | Schema logică pentru full adder>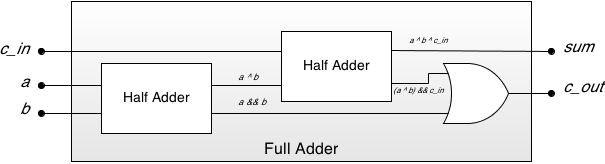 </imgcaption>
</imgcaption>
<hidden Codul C pentru full adder>
void full_adder(int a, int b, int c_in, // inputs int *sum, int *c_out) // outputs { *sum = a ^ b ^ c_in; *c_out = ((a ^ b) & c_in) | (a & b); }
</hidden>
Rulați codul de mai jos (secțiunea hidden) în simulatorul Falstad: Copy la cod → În fereastra de Falstad File>Import apoi Paste și apăsați butonul Import. Rulați și observați funcționarea sumatorului elementar complet.
<hidden (Click aici) Codul pentru simulatorul Falstad pentru sumatorul elementar complet >
$ 1 5.0E-6 1.500424758475255 50 5.0 50 154 352 336 480 336 0 2 0.0 154 544 320 672 320 0 2 0.0 w 480 336 512 336 0 w 512 336 544 336 0 w 544 224 480 224 0 w 544 304 480 304 0 w 480 304 480 288 0 w 480 288 352 288 0 w 480 224 480 288 0 w 496 192 672 192 0 M 800 224 832 224 2 2.5 w 320 352 352 352 0 w 352 176 288 176 0 w 288 176 288 320 0 w 288 320 352 320 0 L 288 320 256 320 2 0 false 5.0 0.0 L 320 352 256 352 2 0 false 5.0 0.0 L 352 288 256 288 2 0 false 5.0 0.0 w 352 208 320 208 0 w 320 208 320 352 0 w 672 192 672 208 0 w 544 256 512 256 0 w 512 256 512 336 0 w 672 320 784 320 0 w 784 320 784 272 0 M 784 272 832 272 2 2.5 150 352 192 496 192 0 2 0.0 150 544 240 672 240 0 2 0.0 152 672 224 800 224 0 2 0.0 x 791 207 855 213 0 24 C_out x 799 308 849 314 0 24 Sum x 185 294 234 300 0 24 C_in x 184 325 197 331 0 24 a x 184 357 198 363 0 24 b
</hidden>
Diagramele Karnaugh pentru so și cout sunt date în tabelele de mai jos:
<tabcaption sum1 center>
| so | ||||
|---|---|---|---|---|
| a0b0/cin | 00 | 01 | 10 | 11 |
| 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
</tabcaption>
<tabcaption sum2 center>
| cout | ||||
|---|---|---|---|---|
| a0b0/cin | 00 | 01 | 10 | 11 |
| 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 |
</tabcaption>
Suma este egală cu 1 atunci când numărul de biți egal cu 1 în procesul de sumare este impar. Transportul cout este egal cu 1 atunci când cel puțin două dintre cele trei intrări (a, b sau cin) au valoarea 1. Datorită distribuției de 1, pentru sumă nu există puncte adiacente, deci funcția este o funcție canonică. În cazul ieșirii de transport, biții se pot cupla și conduce la minimizare.
Din tabelul de mai sus, putem exprima suma prin următoarea formulă:

Această formă canonică necesită 3 nivele de procesare : negație, conjuncție, sumare, pentru a fi adusă într-o formă NAND:


