Prezentarea PowerPoint pentru acest laborator poate fi găsită aici.

utils.py

import base64
 
# CONVERSION FUNCTIONS
def _chunks(string, chunk_size):
    for i in range(0, len(string), chunk_size):
        yield string[i:i+chunk_size]
 
# THIS ONE IS NEW
def byte_2_bin(bval):
    """
      Transform a byte (8-bit) value into a bitstring
    """
    return bin(bval)[2:].zfill(8)
 
def _hex(x):
    return format(x, '02x')
 
def hex_2_bin(data):
    return ''.join(f'{int(x, 16):08b}' for x in _chunks(data, 2))
 
def str_2_bin(data):
    return ''.join(f'{ord(c):08b}' for c in data)
 
def bin_2_hex(data):
    return ''.join(f'{int(b, 2):02x}' for b in _chunks(data, 8))
 
def str_2_hex(data):
    return ''.join(f'{ord(c):02x}' for c in data)
 
def bin_2_str(data):
    return ''.join(chr(int(b, 2)) for b in _chunks(data, 8))
 
def hex_2_str(data):
    return ''.join(chr(int(x, 16)) for x in _chunks(data, 2))
 
# XOR FUNCTIONS
def strxor(a, b):  # xor two strings, trims the longer input
    return ''.join(chr(ord(x) ^ ord(y)) for (x, y) in zip(a, b))
 
def bitxor(a, b):  # xor two bit-strings, trims the longer input
    return ''.join(str(int(x) ^ int(y)) for (x, y) in zip(a, b))
 
def hexxor(a, b):  # xor two hex-strings, trims the longer input
    return ''.join(_hex(int(x, 16) ^ int(y, 16)) for (x, y) in zip(_chunks(a, 2), _chunks(b, 2)))
 
# BASE64 FUNCTIONS
def b64decode(data):
    return bytes_to_string(base64.b64decode(string_to_bytes(data)))
 
def b64encode(data):
    return bytes_to_string(base64.b64encode(string_to_bytes(data)))
 
# PYTHON3 'BYTES' FUNCTIONS
def bytes_to_string(bytes_data):
    return bytes_data.decode()  # default utf-8
 
def string_to_bytes(string_data):
    return string_data.encode()  # default utf-8

In acest laborator veti avea niste exercitii ce folosesc PRFs, PRPs si DES. Puteti sa va uitati in cursul de aici ca sa va aduceti aminte lucrurile de baza.

Fie $F : K × X \to Y$ un $PRF$ sigur cu $K = X = Y = \{0, 1\}^{n}$.

• a) Aratati ca $F_1(k,x) = F(k,x) \| 0$ nu e un $PRF$ sigur.
• b) Aratati ca $F_2(k, x) = F \left(k, x \oplus 1^{n}\right)$ este un $PRF$ sigur.

• c) Fie $K_3 = \{0, 1\}^{n+1}$. Construiti un nou $PRF$ $F_3 : K_3 \times X \to Y$ care sa aiba urmatoarea prorprietate: $PRF$-ul $F_3$ este sigur, dar daca adversarul afla ultimul bit din cheie atunci $PRF$-ul nu mai e sigur. Puteti astfel observa ca pana si aflarea unui singur bit din cheia secreta poate compromite siguranta unui $PRF$ .

• d) Construiti un nou $PRF$ $F_4 : K × X \to Y$ care ramane sigur chiar si atunci cand atacatorul cunoaste unul (oricare) dintre bitii cheiei. Functia voastra $F_4$ trebuie sa cheme o singura data functia $F$. Explicati de ce ramane un $PRF$ sigur chiar si dupa aceasta scurgere de informatie.

Vom analiza acum retele substitutie-permutare (SPN - substitution-permutation networks)

We have the SPN from this figure:

where S denotes the AES S-box (we'll discuss this in some detail during the next lecture), and 'Permutation' is a simple permutation block that simply shifts the input 4 bits to the right as in a queue. Both this S-box and the permutation are invertible and known by the attacker (you). Each input (x1, x2) is 8-bit (1 byte), as well as the keys k1, k2, and the outputs y1, y2.

1. How can you find the key ?
2. Given the message/ciphertext pair ('Hi' - as characters, 0xba52 - as hex number), find the key bytes k1 and k2. Print them in ascii.

spn1.py

from utils import *
 
# Rijndael S-box
sbox = [0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67,
        0x2b, 0xfe, 0xd7, 0xab, 0x76, 0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59,
        0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0, 0xb7,
        0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1,
        0x71, 0xd8, 0x31, 0x15, 0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05,
        0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75, 0x09, 0x83,
        0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29,
        0xe3, 0x2f, 0x84, 0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b,
        0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf, 0xd0, 0xef, 0xaa,
        0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c,
        0x9f, 0xa8, 0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc,
        0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2, 0xcd, 0x0c, 0x13, 0xec,
        0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19,
        0x73, 0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee,
        0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb, 0xe0, 0x32, 0x3a, 0x0a, 0x49,
        0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79,
        0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4,
        0xea, 0x65, 0x7a, 0xae, 0x08, 0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6,
        0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a, 0x70,
        0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9,
        0x86, 0xc1, 0x1d, 0x9e, 0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e,
        0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf, 0x8c, 0xa1,
        0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0,
        0x54, 0xbb, 0x16]
 
# Rijndael Inverted S-box
rsbox = [0x52, 0x09, 0x6a, 0xd5, 0x30, 0x36, 0xa5, 0x38, 0xbf, 0x40, 0xa3,
         0x9e, 0x81, 0xf3, 0xd7, 0xfb, 0x7c, 0xe3, 0x39, 0x82, 0x9b, 0x2f,
         0xff, 0x87, 0x34, 0x8e, 0x43, 0x44, 0xc4, 0xde, 0xe9, 0xcb, 0x54,
         0x7b, 0x94, 0x32, 0xa6, 0xc2, 0x23, 0x3d, 0xee, 0x4c, 0x95, 0x0b,
         0x42, 0xfa, 0xc3, 0x4e, 0x08, 0x2e, 0xa1, 0x66, 0x28, 0xd9, 0x24,
         0xb2, 0x76, 0x5b, 0xa2, 0x49, 0x6d, 0x8b, 0xd1, 0x25, 0x72, 0xf8,
         0xf6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xd4, 0xa4, 0x5c, 0xcc, 0x5d,
         0x65, 0xb6, 0x92, 0x6c, 0x70, 0x48, 0x50, 0xfd, 0xed, 0xb9, 0xda,
         0x5e, 0x15, 0x46, 0x57, 0xa7, 0x8d, 0x9d, 0x84, 0x90, 0xd8, 0xab,
         0x00, 0x8c, 0xbc, 0xd3, 0x0a, 0xf7, 0xe4, 0x58, 0x05, 0xb8, 0xb3,
         0x45, 0x06, 0xd0, 0x2c, 0x1e, 0x8f, 0xca, 0x3f, 0x0f, 0x02, 0xc1,
         0xaf, 0xbd, 0x03, 0x01, 0x13, 0x8a, 0x6b, 0x3a, 0x91, 0x11, 0x41,
         0x4f, 0x67, 0xdc, 0xea, 0x97, 0xf2, 0xcf, 0xce, 0xf0, 0xb4, 0xe6,
         0x73, 0x96, 0xac, 0x74, 0x22, 0xe7, 0xad, 0x35, 0x85, 0xe2, 0xf9,
         0x37, 0xe8, 0x1c, 0x75, 0xdf, 0x6e, 0x47, 0xf1, 0x1a, 0x71, 0x1d,
         0x29, 0xc5, 0x89, 0x6f, 0xb7, 0x62, 0x0e, 0xaa, 0x18, 0xbe, 0x1b,
         0xfc, 0x56, 0x3e, 0x4b, 0xc6, 0xd2, 0x79, 0x20, 0x9a, 0xdb, 0xc0,
         0xfe, 0x78, 0xcd, 0x5a, 0xf4, 0x1f, 0xdd, 0xa8, 0x33, 0x88, 0x07,
         0xc7, 0x31, 0xb1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xec, 0x5f, 0x60,
         0x51, 0x7f, 0xa9, 0x19, 0xb5, 0x4a, 0x0d, 0x2d, 0xe5, 0x7a, 0x9f,
         0x93, 0xc9, 0x9c, 0xef, 0xa0, 0xe0, 0x3b, 0x4d, 0xae, 0x2a, 0xf5,
         0xb0, 0xc8, 0xeb, 0xbb, 0x3c, 0x83, 0x53, 0x99, 0x61, 0x17, 0x2b,
         0x04, 0x7e, 0xba, 0x77, 0xd6, 0x26, 0xe1, 0x69, 0x14, 0x63, 0x55,
         0x21, 0x0c, 0x7d]
 
 
def permute4(s):
    """
      Perform a permutatation by shifting all bits 4 positions right.
      The input is assumed to be a 16-bit bitstring
    """
    ps = ''
    ps = ps + s[12:16]
    ps = ps + s[0:12]
    return ps
 
 
def permute_inv4(s):
    """
      Perform the inverse of permute4
      The input is assumed to be a 16-bit bitstring
    """
    ps = ''
    ps = ps + s[4:16]
    ps = ps + s[0:4]
    return ps
 
 
def spn_1r_reduced_2s(k, x):
    """
      Performs an encryption with a substitution-permutation network.
      Key k = {k1, k2}, total of 16 bits (2 x 8 bits)
      Input x = {x1, x2}, total of 16 bits (2 x 8 bits)
      Both k and x are assumed to be bitstrings.
 
      Return:
      a 16-bit bitstring containing the encryption y = {y1, y2}
    """
 
    # Split input and key
    x1 = x[0:8]
    x2 = x[8:16]
    k1 = k[0:8]
    k2 = k[8:16]
 
    # Apply S-box
    u1 = bitxor(x1, k1)
    v1 = sbox[int(u1, 2)]
    v1 = byte_2_bin(v1)
 
    u2 = bitxor(x2, k2)
    v2 = sbox[int(u2, 2)]
    v2 = byte_2_bin(v2)
 
    # Apply permutation
    pin = v1 + v2
    pout = permute4(pin)
 
    return pout
 
 
def spn_1r_full_2s(k, x):
    """
      Performs an encryption with a substitution-permutation network.
      Key k = {k1, k2, k3, k4}, total of 32 bits (4 x 8 bits)
      Input x = {x1, x2}, total of 16 bits (2 x 8 bits)
      Both k and x are assumed to be bitstrings.
 
      Return:
      a 16-bit bitstring containing the encryption y = {y1, y2}
    """
 
    # Split input and key
    x1 = x[0:8]
    x2 = x[8:16]
    k1 = k[0:8]
    k2 = k[8:16]
    k3 = k[16:24]
    k4 = k[24:32]
 
    # Apply S-box
    u1 = bitxor(x1, k1)
    v1 = sbox[int(u1, 2)]
    v1 = byte_2_bin(v1)
 
    u2 = bitxor(x2, k2)
    v2 = sbox[int(u2, 2)]
    v2 = byte_2_bin(v2)
 
    # Apply permutation
    pin = v1 + v2
    pout = permute4(pin)
 
    # Apply final XOR
    po1 = pout[0:8]
    po2 = pout[8:16]
    y1 = bitxor(po1, k3)
    y2 = bitxor(po2, k4)
 
    return y1+y2
 
 
def main():
 
    # Run reduced 2-byte SPN
    msg = 'Hi'
    key = '??'  # Find this
    xs = str_2_bin(msg)
    ks = str_2_bin(key)
    ys = spn_1r_reduced_2s(ks, xs)
    print('Two y halves of reduced SPN: ' + ys[0:8] + ' (hex: ' + bin_2_hex(
        ys[0:8]) + '), ' + ys[8:16] + ' (hex: ' + bin_2_hex(ys[8:16]) + ')')
 
    # Run full 2-byte SPN
    msg = 'Om'
    key = '????'  # Find this
    xs = str_2_bin(msg)
    ks = str_2_bin(key)
    ys = spn_1r_full_2s(ks, xs)
    print('Two y halves of full SPN (2 bytes): ' + ys[0:8] + ' (hex: ' + bin_2_hex(
        ys[0:8]) + '), ' + ys[8:16] + ' (hex: ' + bin_2_hex(ys[8:16]) + ')')
 
 
if __name__ == "__main__":
    main()  

Now we have a better SPN, where the output of the permutation is XOR-ed with another 2 key bytes, as in the following figure:

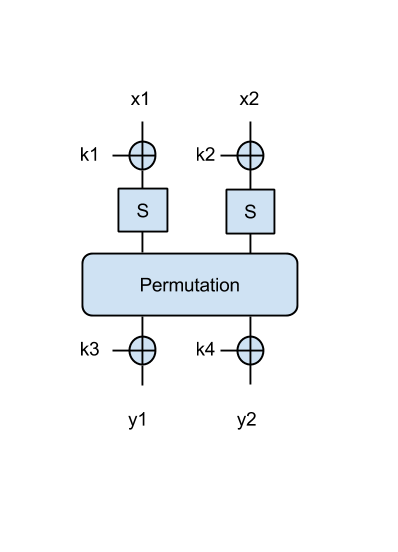
1. Try to find the key in this case, when given the following message/ciphertext pairs: ('Om', 0x0073), ('El', 0xd00e), ('an', 0x855b). Print the key in ascii.

As another example, which uses a larger block size, let's use an SPN that takes a 4-byte input x=[x1 || x2 || x3 || x4] and an 8-byte key k=[k1 || k2 || k3 || k4 || k5 || k6 || k7 || k8] as in this figure:

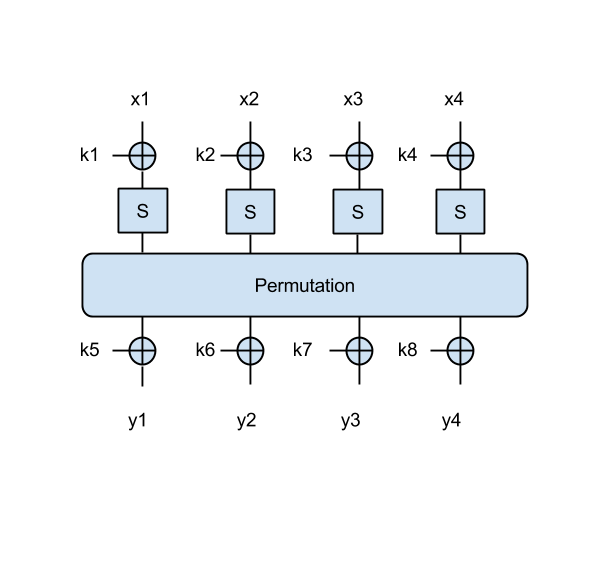
Note that in this 4-byte SPN, the permutation operates on all 4 bytes, similarly to the 2-byte SPN: that is, it shifts all bits four bits to the right.

1. Try to find the key in this case as well, using the following message/ciphertext pairs: ('Omul', 0xddcf7bc7), ('stea', 0x96d58b43), ('luna', 0x9c3f2303) . Again print the key in ascii.