Laborator 09: Drumuri minime în grafuri: surse / destinații multiple. (2/2)

Changing the world through digital experiences is what Adobe’s all about. We give everyone - from emerging artists to global brands - everything they need to design and deliver exceptional digital experiences! We’re passionate about empowering people to create beautiful and powerful images, videos, and apps, and transform how companies interact with customers across every screen.
Obiective laborator
În laboratorul anterior am introdus contextul pentru Shortest-paths problem și Single-source shortest-paths problem. În laboratorul 10 vom continua cu All-pairs shortest-paths problem.
- Înțelegerea conceptelor de cost asociat unei muchii, relaxare a unei muchii.
- Prezentarea problemei drumului de cost minim (diverse variante).
- Prezentarea algoritmilor pentru calculul drumurilor minime.
Shortest-paths problem: all-pairs
Vă rugăm să parcugeți Shortest-paths problem pentru a vă familiariza cu contextul, problema și notațiile folosite.
Concepte necesare:
- cost muchie / edge cost
- cost drum / path cost
- problema drumurilor minime: surse / destinații multiple / all-pairs shortest-paths problem
- relaxarea unei muchii / edge relaxation
- reconstruirea unui drum / RebuildPath
Algoritmi
În acest laborator vom studia all-pairs shortest-paths problem. Pentru această problemă, vom prezenta 2 algoritmi:
- Roy-Floyd: eficient pentru grafuri dense ($m >> n$ sau $|E| >> |V|$ - a.k.a. număr de muchii mult mai decât număr de noduri).
- Johnson: eficient pentru grafuri rare ($n >> m$ sau $|V| >> |E|$ - a.k.a. număr de noduri mult mai mare decât număr de muchii).
Vom prezenta fiecare algoritm, îl vom analiza, iar la final vom vedea când îl vom folosi pe fiecare.
Puteți consulta capitolul All-Pairs Shortest Paths din Introduction to Algorithms [0] pentru mai multe detalii despre acești algoritmi.
Roy-Floyd
Algoritmul Roy-Floyd (Roy-Floyd / Floyd–Warshall algorithm) rezolvă shortest-paths problem în grafuri G = (V, E) care sunt dense.
Roy-Floyd - Pseudocod
// apply Roy-Floyd's algorithm for all-pairs shortest-paths problem // // nodes = list of all nodes from G // adj[node] = the adjacency list of node // example: adj[node] = {..., neigh, ...} => edge (node, neigh) of cost w[node][neigh] // // // returns: d, p // d = distance matrix // p = parent matrix // Roy-Floyd(G=(nodes, adj)) { // STEP 1: initialize results // d[i][j] = minimum distance from i to j // p[i][j] = parent of node j, on shortest path from i to j for (i in nodes) { for (j in nodes) { d[i][j] = w[i][j]; // edge cost (or infinity if missing) p[i][j] = (w[i][j] != infinity ? i : null); // parent (or null if missing) } } // STEP 2: For each intermediar node k, // try to update shortest path from i to j. for (k in nodes) { for (i in nodes) { for (j in nodes) { // Is (i -> ... -> k) reunion with (k -> ... -> j) shorter than (i -> ... -> j)? if (d[i][k] + d[k][j] < d[i][j]) { d[i][j] = d[i][k] + d[k][j]; p[i][j] = p[k][j]; } } } } return d, p; } // Usage example: d, p = Roy-Floyd(G=(nodes, adj)); // 1. Use distances from d // 2. Rebuild path from node to source using parents (p) RebuildPath(source, destination, p);
Exemple
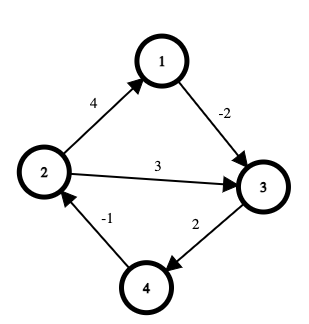
Exemplu Roy-Floyd
Complexitate
- complexitate temporală: $T = O(n^3)\ sau\ O(|E|^3)$
- complexitate spațială : $S = O(1)$
Johnson
Algoritmul lui Johnson (Johnson’s algorithm) rezolvă shortest-paths problem în grafuri G = (V, E) care sunt rare.
Ideea de la care pornește acest algoritm este de a rula cel mai rapid algorithm pentru shortest-paths single source, adică algoritmul lui Dijkstra, pentru fiecare sursă (nod) din graf. Dacă toate costurile sunt pozitive, putem face direct acest lucru. Dacă însă există costuri negative, nu putem aplica Dijkstra pe acest graf. Algoritmul lui Johnson face o preprocesare (în ComputeH) și calculează un graf echivalent, în care toate costurile sunt pozitive. Pe acest graf se poate aplica Dijkstra și să se afle toate distanțele. Ulterior se face translatarea inversă și se obțin distanțele în graful inițial.
Observație: Dacă se știe că toate costurile din graf sunt pozitive (nenegative), algoritmul lui Johnson se poate înlocui cu rularea directă a algoritmului Dijkstra pentru toate nodurile din graf.
Johnson - Pseudocod
// apply Johnson's algorithm for all-pairs shortest-paths problem // // nodes = list of all nodes from G // adj[node] = the adjacency list of node // example: adj[node] = {..., neigh, ...} => edge (node, neigh) of cost w[node][neigh] // // returns: has_cycle, d, p // has_cycle = negative cycle detection flag (true if found) // d = distance matrix (defined only if has_cycle == false) // p = parent matrix (defined only if has_cycle == false) // Johnson(G=(nodes, adj)) { // STEP 1: Compute adjustment distances h (using Bellmand-Ford). has_cycle, h = ComputerH(G); if (has_cycle) { return true, null, null; } // STEP 2: Update all costs in G to obtain all costs nonnegative. foreach ((u, v) in edges) { if (w[u][v] != infinity) { w[u][v] = w[u][v] + (h[u] - h[v]); } } // STEP 3: Now all costs are nonnegative, so we can apply Dijsktra. // Start Dijkstra for each source u, saving just distances. foreach (u in nodes) { d_dijkstra, p_dijkstra = Dijkstra(u, G); // STEP 4: Compute distance (u, v) on initial graph. foreach (v in nodes) { d[u][v] = d_dijkstra[v] + (h[v] - h[u]); p[u][v] = p_dijkstra[v]; } } return false, d, p; // no negative cycles detected } ComputeH(G=(nodes, adj)){ // STEP 0: Create a new **temporary** graph // * add a new node source = new node; new_nodes = nodes + { source }; new_adj = adj; // * add a new edge (source, node) with cost 0 for all existing nodes for (node in nodes) { new_adj[source].push_back(node); w[source][node] = 0; } // STEP 1: Run Bellman-Ford on the new graph. Save just flag and distances. has_cycle, h, _ = Bellmann-Ford(source, new_G=(new_nodes, new_adj))) if (has_cycle) { return true, null; // negative cycle detected } return false, d; } // Usage example: has_cycle, d, p = Johnson(source, G=(nodes, adj)); if (has_cycle) { print "Has Cycle!" STOP. } else { // 1. Use distances from d // (e.g. d[node] = distance from source to node) // // 3. Rebuild path from node to source using parents (p) RebuildPath(source, destination, p); }
Exemple
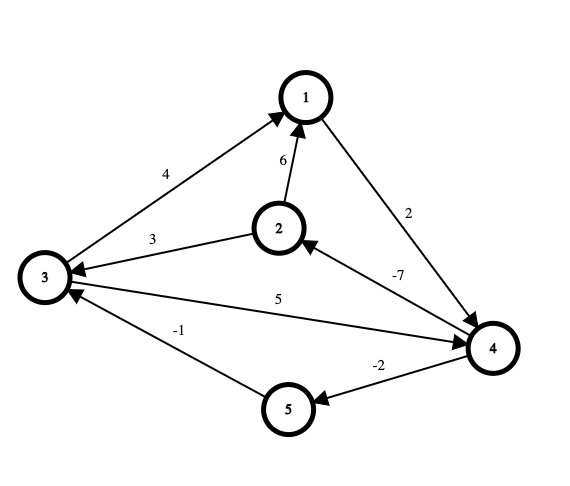
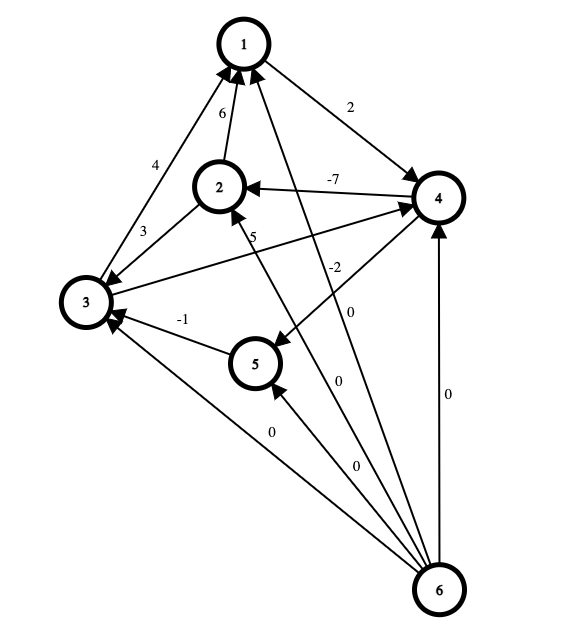
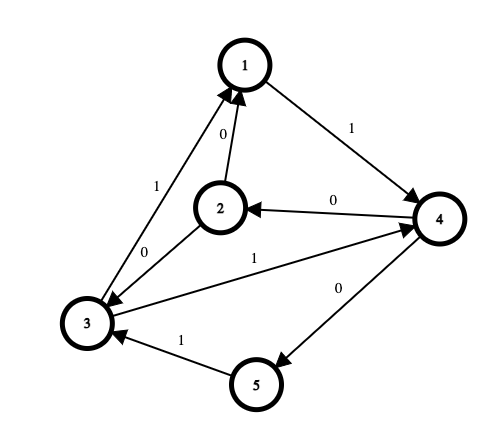
Exemplu Johnson
În această secțiune exemplificăm grafic cum rulează algoritmul lui Johnson pe un graf dat.
Complexitate
- complexitate temporală: $T = O(n * m * log (n))\ sau\ O(|V| * |E| * log (|V|))$
- complexitate spațială : $S = O(n + m)\ sau \ O(|V| + |E|)$
TLDR
- Pentru cazul shortest-path single source am studiat în laboratorul anterior algoritmul lui Dijkstra / algoritmul Bellman-Ford.
- Pentru cazul shortest-path all-pairs, discuția se facă după numărul de muchii din graf:
- graf dens: aplicăm Roy-Floyd și obținem $O(n ^ 3)$.
- graf rar: aplicăm Johnson și obținem $O(n * m * log (n))$.
Exerciții
Scheletul de laborator se găsește pe pagina pa-lab::skel/lab10.
Înainte de a rezolva exercițiile, asigurați-vă că ați citit și înțeles toate precizările din secțiunea Precizari laboratoare 07-12.
Prin citirea acestor precizări vă asigurați că:
- știți convențiile folosite
- evitați buguri
- evitați depunctări la lab/teme/test
Roy-Floyd
Se dă un graf orientat cu n noduri. Graful are costuri strict pozitive.
Se dă matricea ponderilor - w, se cere matricea drumurilor minime - d, aplicând algoritmul Roy-Floyd.
Restricții și precizări:
- $ n <= 100 $
- $ 0 <= c <= 1.000$, unde c este costul unui arc.
- Dacă nu există arc între o pereche de noduri x și y, distanța de la nodul x la nodul y din matricea ponderilor va fi 0.
- Dacă după aplicarea algoritmului nu se găsește drum pentru o pereche de noduri x și y, se va considera distanța dintre ele egală cu 0 (se stochează în matricea distantelor valoarea 0).
- Drumul de la nodul i la nodul i are lungime 0 (prin convenție).
- timp de execuție
- C++: 1s
- Java: 8s
Johnson
Se dă un graf orientat cu n noduri. Graful are costuri oarecare (pot fi și negative).
Se dă lista de adiacență cu costurile aferente, se cere matricea drumurilor minime - d, aplicând algoritmul Johnson.
Restricții și precizări:
- $ n <= 1000 $
- $ m <= 25000 $
- $ -1000 <= c <= 1.000$, unde c este costul unui arc.
- Dacă nu există arc între o pereche de noduri x și y, distanța de la nodul x la nodul y din matricea ponderilor va fi 0.
- Dacă după aplicarea algoritmului nu se găsește drum pentru o pereche de noduri x și y, se va considera distanța dintre ele egală cu 0 (se stochează în matricea distantelor valoarea 0).
- Drumul de la nodul i la nodul i are lungime 0 (prin convenție).
- Dacă graful conține un ciclu de cost negativ, se va afișa mesajul: Ciclu negativ!
- timp de execuție
- C++: 1s
- Java: 8s
BONUS
La acest laborator, asistentul va alege 1-2 probleme din secțiunea extra.
Extra
Referințe
[0] Chapters Single-Source Shortest Paths / All-Pairs Shortest Paths, “Introduction to Algorithms”, Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest and Clifford Stein.