Responsabili:

• Darius Neațu (2019-2020)
• Dorinel Filip (2019-2020)
• Andrei Pârvu

În urma parcurgerii acestui laborator, studentul va fi capabil:

• să declare şi să iniţializeze vectori/matrici (din declaraţie şi prin structuri iterative)
• să implementeze algoritmi simpli de sortare şi căutare pe vectori
• să folosească practici recunoscute şi recomandate pentru scrierea de cod sursă care implică lucrul cu tablouri
• să recunoască şi să evite erorile comune de programare legate de aceste structuri
• sa cunoască regulile de reprezentare ale tablourilor în memorie și să înteleagă modul în care compilatorul interpretează operatorii de indexare;

Printr-un vector se înţelege o colecţie liniară şi omogenă de date. Un vector este liniar pentru că datele(elementele) pot fi accesate în mod unic printr-un index. Un vector este, de asemenea, omogen, pentru că toate elementele sunt de acelaşi tip. În limbajul C, indexul este un număr întreg pozitiv şi indexarea se face începând cu 0.

Declaraţia unei variabile de tip vector se face în felul următor:

<tip_elemente> <nume_vector>[<dimensiune>];

De exemplu, avem următoarele declaraţii de vectori:

int a[100];
float vect[50];
 
#define MAX 100
...
unsigned long numbers[MAX];

Este de remarcat că vectorul este o structură statică: dimensiunea acestuia trebuie să fie o constantă la compilare şi nu poate fi modificată în cursul execuţiei programului. Astfel, programatorul trebuie să estimeze o dimensiune maximă pentru vector, şi aceasta va fi o limitare a programului. De obicei, se folosesc constante simbolice (ca în ultimul exemplu) pentru aceste dimensiuni maxime, pentru ca ele să poată fi ajustate uşor la nevoie. De asemenea, în cadrul unei declaraţii, se pot iniţializa cu valori constante componente ale vectorului, iar în acest caz, dimensiunea vectorului poate rămâne neprecizată (compilatorul o va determina din numărul elementelor din listă). De exemplu:

int a[3] = {1, 5, 6};                     // Toate cele 3 elemente sunt initializate 
float num[] = {1.5, 2.3, 0.2, -1.3};      // Compilatorul determina dimensiunea - 4 - a vectorului
unsigned short vect[1000] = {0, 2, 4, 6}; // Sunt initializate doar primele 4 elemente, iar toate celelalte sunt initializate cu valoarea 0

În cazul special în care specificăm dimensiunea şi doar un singur element la initializare, primul element va fi cel specificat, iar toate celelalte elemente ale vectorului vor fi iniţializate la 0:

char string[100] = {97}; // Sirul va fi initializat cu: 97 (caracterul 'a') pe prima poziţie şi 99 de 0
int v[100] = {0};        // Vectorul va fi umplut cu 0.

Este important de remarcat faptul că elementele neiniţializate pot avea valori oarecare. La alocarea unui vector, compilatorul nu efectuează nici un fel de iniţializare şi nu furnizează nici un mesaj de eroare dacă un element este folosit înainte de a fi iniţializat. Un program corect va iniţializa, în orice caz, fiecare element înainte de a-l folosi. Elementele se accesează prin expresii de forma <nume_vector>[<indice>]. De exemplu, putem avea:

char vect[100];
vect[0] = 1;
vect[5] = 10;
 
int i = 90;
vect[i] = 15;
vect[i + 1] = 20;

Citirea unui vector de intregi de la tastatura:

int main() 
{
  int a[100], n, i; /* vectorul a are maxim 100 de intregi */
 
  scanf("%d", &n); /* citeste nr de elemente vector */
 
  for (i = 0; i < n; i++) {
    scanf("%d", &a[i]); /* citire elemente vector */
  }
 
  for (i = 0; i < n; i++) {
    printf("%d ", a[i]); /* scrie elemente vector */
  }
 
  return 0;
}

Generarea unui vector cu primele n numere Fibonacci:

#include <stdio.h>
int main() 
{
  long fib[100] = {1, 1};
  int n, i;
 
  printf("n = "); 
  scanf("%d", &n);
 
  for (i = 2; i < n; i++) {
    fib[i] = fib[i - 1] + fib[i - 2];
  }
  for (i = 0; i < n; i++) {
    printf("%ld ", fib[i]);
  }
 
  return 0;
}

• Depăşirea limitelor indicilor (index out of bounds) este o eroare frecventă, ce poate duce la blocarea programului sau a sistemului şi poate fi evitată prin verificarea încadrării în intervalul valid.
• Indici folosiţi greşit în bucle imbricate (index cross-talk). Sunt multe cazuri în care pe un nivel al buclei se foloseşte, de exemplu vect[i], şi pe nivelul imbricat vect[j], când de fapt se dorea folosirea lui i. Mare atenţie şi în astfel de cazuri!

#define MAX   100
 
int vect[MAX];

va fi de preferat în locul lui

int vect[100];

Exemplu:

// program care citeşte un index şi o valoare, şi atribuie valoarea elementului din vector care se găseşte la poziţia respectivă
#include <stdio.h>
#define N 10
 
int main() 
{
  int i, val;
  int v[N];
 
  scanf("%d%d", &i, &val);
 
  /* !!! Verific daca indexul este valid */
  if (i >= 0 && i < N) {
   v[i] = val;
  } else {
    printf("Introduceti un index >= 0 si < %d\n", N);
  }
 
  return 0;
}

Exemplu:

#include <stdio.h>
#define N 100
 
int main() 
{
  int v[N];
  int i, j; /* indecsii elementelor ce vor fi interschimbate */
  int aux;  /* variabila ajutatoare pentru interschimbare */
 
  /*... initializari */
 
  /* Interschimb */
  aux = v[i];
  v[i] = v[j];
  v[j] = aux;
 
  return 0;
}

Când avem de a face cu un vector nesortat (şi nu numai în acest caz), cea mai simplă abordare pentru a găsi o valoare, este căutarea secvenţială. Cu alte cuvinte, se compară, la rând, fiecare valoare din vector cu valoarea căutată. Dacă valoarea a fost găsită, căutarea se poate opri (nu mai are sens să parcugem vectorul până la capăt, dacă nu se cere acest lucru explicit).

Exemplu:

#define MAX 100
 
...
 
int v[MAX], x, i;
 
/* initializari */
...
 
int found = 0;
for (i = 0; i < MAX; i++) {
  if (x == v[i]) {
    found = 1;
    break;
  }
}
 
if (found) {
   printf("Valoarea %d a fost gasita in vector\n", x);
} else { 
   printf("Valoarea %d nu a fost gasita in vector\n", x);
}
...

Dacă vectorul pe care se face căutarea este sortat, algoritmul mai eficient de folosit în acest caz este căutarea binară. Presupunem că vectorul este sortat crescător (pentru vectori sortaţi descrescător, raţionamentul este similar).

Valoarea căutată, x, se compară cu valoarea cu indexul N/2 din vector, unde N este numărul de elemente. Dacă x este mai mic decât valoarea din vector, se caută în prima jumătate a vectorului, iar dacă este mai mare, în cea de-a doua jumătate. Căutarea în una dintre cele două jumătăţi se face după acelaşi algoritm.

Conceptual, căutarea binară este un algoritm recursiv, dar poate fi implementat la fel de bine într-un mod iterativ, folosind indecşii corespunzători bucăţii din vector în care se face căutarea. Aceşti indecşi se modifică pe parcursul algoritmului, într-o buclă, în funcţie de comparaţiile făcute. Evoluţia algoritmului este ilustrată în imaginea de mai jos.

Pseudocodul pentru căutarea binară:

// cauta elementul x in vectorul sortat v, intre pozitiile 0 si n-1  si returneaza pozitia gasita sau -1
int binary_search(int n, int v[NMAX], int x) {
  int low = 0, high = n - 1;
 
  while (low <= high) {
    // De ce preferăm această formă față de (low + high) / 2 ?
    int middle = low + (high - low) / 2;
 
    if (v[middle] == x) {
      // Am gasit elementul, returnam pozitia sa
      return middle;
    }
 
    if (v[middle] < x) {
      // Elementul cautat este mai mare decat cel curent, ne mutam in jumatatea
      // cu elemente mai mari
      low = middle + 1;
    } else {
      // Elementul cautat este mai mic decat cel curent, ne mutam in jumatatea
      // cu elemente mai mici
      high = middle - 1;
    }
  }
 
  // Elementul nu a fost gasit
  return -1;
}

Metoda bulelor este cea mai simplă modalitate de sortare a unui vector, dar şi cea mai ineficientă. Ea funcţionează pe principiul parcurgerii vectorului şi comparării elementului curent cu elementul următor. Dacă cele două nu respectă ordinea, sunt interschimbate. Această parcurgere este repetată de suficiente ori până când nu mai există nici o interschimbare în vector.

Sortarea prin selecţie oferă unele îmbunătăţiri în ceea ce priveşte complexitatea, însă este departe de a fi considerat un algoritm eficient. Presupunând că se doreşte sortarea crescătoare a vectorului, se caută minimul din vector, şi se interschimbă cu primul element - cel cu indexul 0. Apoi se reia acelaşi procedeu pentru restul vectorului. Motivul pentru care algoritmul de sortare prin selecţie este mai eficient este acela că vectorul în care se caută minimul devine din ce în ce mai mic, şi, evident, căutarea se face mai repede la fiecare pas.

Studiul unor algoritmi mai avansaţi de sortare, precum şi studiul complexităţii lor nu constituie obiectul acestui laborator. Acestea se vor relua mai detaliat în cadrul altor cursuri (AA/PA).

Responsabili:

• Darius Neațu (CA 2019-2020)
• Dorinel Filip (CA 2019-2020)
• Andrei Pârvu

Probleme

Teste

Matricea este o colecţie omogenă şi bidimensională de elemente. Acestea pot fi accesate prin intermediul a doi indici, numerotaţi, ca şi în cazul vectorilor, începand de la 0. Declaraţia unei matrice este de forma:

<tip_elemente> <nume_matrice>[<dim_1>][<dim_2>];

De exemplu, avem:

int mat[5][10];

#define MAX_ELEM 100
float a[MAX_ELEM][MAX_ELEM];

Numărul de elemente ale unei matrice va fi dim_1*dim_2, şi semnificaţia fiecărei dimensiuni este o chestiune ce ţine de logica programului. În matematică, prima dimensiune poate să însemne linia şi a doua coloana pentru fiecare element, însa acest lucru nu este obligatoriu. Este necesar totuşi, pentru funcţionarea corectă a programului, să se respecte semnificaţiile alese pe întreg parcursul codului sursă.

Vectorii şi matricele se pot extrapola la noţiunea generală de tablou cu mai multe dimensiuni, care se declară în modul următor:

<tip_elemente> <nume_tablou>[<dim_1>][<dim_2>]...[<dim_n>];

De exemplu:

int cube[3][3][3];

Deşi, în cazul a mai mult de 3 dimensiuni, tablourile pot să nu mai aibă sens concret sau fizic, acestea pot fi deosebit de utile în multe situaţii. În acest laborator ne vom rezuma totuşi la tablouri bidimensionale.

Fie $A \in {\mathbb R}^{m \times n}$, $B \in {\mathbb R}^{m \times n}$, atunci $(A+B) \in {\mathbb R}^{m \times n}$, unde: $(A+B)_{i,j} = A_{i,j} + B_{i,j}$

Exemplu:

$$ \Large \begin{bmatrix} 1 & 3 \\ 0 & 4 \\ 5 & 8 \end{bmatrix} + \begin{bmatrix} 2 & 5 \\ 1 & 2 \\ 6 & 1 \end{bmatrix} = \begin{bmatrix} 3 & 8 \\ 1 & 6 \\ 11 & 9 \end{bmatrix} $$

Fie $A \in {\mathbb R}^{m \times n}$, $B \in {\mathbb R}^{n \times p}$, atunci $(AB) \in {\mathbb R}^{m \times p}$, unde elementele $A.B$ sunt date de formula: $(AB)_{i,j} = \sum_{r=1}^n A_{i,r}B_{r,j}$

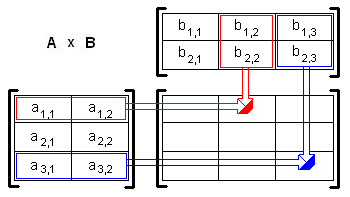Exemplul din stânga prezintă cum se calculează valorile (1,2) si (3,3) ale 'AB' daca 'A' este o matrice 3×2, si 'B' o matrice 2×3. Pentru calculul unui element din matrice se consideră o linie respectiv o coloană din fiecare matrice conform săgeţilor. Elementele din acestea sunt înmulţite câte 2 conform înmulţirii pe vectori, apoi suma produselor constituie elementul din matricea finală

$$ (\mathbf{AB})_{1,2} = \sum_{r=1}^2 a_{1,r}b_{r,2} = a_{1,1}b_{1,2}+a_{1,2}b_{2,2} \\ (\mathbf{AB})_{3,3} = \sum_{r=1}^2 a_{3,r}b_{r,3} = a_{3,1}b_{1,3}+a_{3,2}b_{2,3} $$

Exemplu:

$$ \Large \begin{bmatrix} 1 & 0 & 2 \\ -1 & 3 & 1 \end{bmatrix} \cdot \begin{bmatrix} 3 & 1 \\ 2 & 1 \\ 1 & 0 \end{bmatrix} = \begin{bmatrix} 1 \times 3 + 0 \times 2 + 2 \times 1 & 1 \times 1 + 0 \times 1 + 2 \times 0 \\ -1 \times 3 + 3 \times 2 + 1 \times 1 & -1 \times 1 + 3 \times 1 + 1 \times 0 \end{bmatrix} = \begin{bmatrix} 5 & 1 \\ 4 & 2 \end{bmatrix} $$

Cunoaşterea reprezentării în memorie a tablourilor vă ajută să înţelegeţi mai bine cum se lucrează cu aceste tipuri de date şi să evitaţi atât erorile comune, cât şi pe cele mai subtile. Aşa cum se ştie, fiecare variabilă are asociata o anumită adresă în memorie şi ocupă o anumită lungime, măsurată în octeţi. Standardul C impune ca un tablou să fie memorat într-o zonă continuă de memorie, astfel ca pentru un tabloul de forma: T tab[dim1][dim2]…[dimn]; dimensiunea ocupată în memorie va fi sizeof(T)*dim1*dim2*…*dimn. Vom considera în continuare cazul particular al unui vector vect de lungime n, şi al unui element oarecare al acestuia, de pe pozitia i. Atunci când întalneşte numele vect, compilatorul va intelege “adresa în memorie de la care începe vectorul vect”. Operatorul de indexare [] aplicat numelui vect instruieşte compilatorul să “evalueze acel element de tipul T, care se află pe pozitia i în vectorul care începe de la adresa vect”. Acest lucru se poate exprima direct: “evaluarea variabilei de tip T de la adresa vect + i * sizeof(T)”.

În ultima formulare observaţi ca nu mai intervine sub nici o formă dimensiunea vectorului dată la declarare. Aceea a fost necesară doar compilatorului, ca sa ştie câtă memorie să aloce pentru reprezentarea acestuia. De asemenea, observaţi că sunt permise indexari în afara spaţiului de memorie alocat, şi astfel programul va putea, din greşeala, accesa alte zone de memorie, lucru care poate avea repercursiuni grave. În cel mai bun caz programul nostru se va comporta foarte ciudat (erori în locuri total imprevizibile), şi în cel mai rău caz întreg sistemul va fi blocat (în cazul sistemelor care nu au implementate spaţii virtuale de memorie proprii fiecărei aplicaţii - platformele Windows NT si Linux).

Faptul că graniţa dintre vectori şi adrese de memorie este atât de fină în limbajul C, sintaxa acestuia permite expresii ciudate, de forma:

char a[100];
a[0] = 1;
3[a] = 5;

Instrucţiunea din urmă înseamna pur şi simplu “asignează 5 variabilei de tip char de la adresa 3 + a * sizeof(char) = 3 + a”. Observaţi că aceasta este echivalentă cu a[3] = 5;

De asemenea, un alt avantaj apare la definirea unui parametru al unei funcţii, de tip vector, caz în care nu este necesară precizarea dimensiunii acestuia: void sort(int[] vect, n);

• Declararea unei matrici unitate:

#define M 20 /* nr maxim de linii si de coloane */
 
int main() {
  float unit[M][M];
  int i,j,n;
 
  printf("nr.linii/coloane: ");
  scanf("%d", &n);
  if (n > M) {
    return;
  }
 
  for (i = 0; i < n; i++) {
    for (j = 0; j < n; j++) {
      if (i != j) {
        unit[i][j]=0;
      } else {
        unit[i][j]=1;
      }
    }
  }
 
  return 0;
}

• Citire/scriere de matrice de reali:

int main() {
  int nl, nc, i, j;
  float a[20][20];
 
  /* Citire de matrice */
  printf("nr.linii: ");
  scanf("%d", &nl);
  printf("nr.coloane: ");
  scanf("%d", &nc);
 
  if (nl > 20 || nc > 20) {
    printf("Eroare: dimensiuni > 20 \n");
    return ;
  }
 
  for (i = 0; i < nl; i++) {
    for (j = 0; j < nc; j++) {
      scanf("%f", &a[i][j]);
    }
  }
 
  /* Afisare matrice */
  for (i = 0; i < nl; i++) {
    for (j = 0; j < nc; j++) {
      printf("%f ",a[i][j]);
    }
    printf ("\n");
  }
 
  return 0;
}

• Inversarea indicilor pentru elementele unei matrice sau tablou. E usor sa-l inversezi pe i cu j in expresia A[i][j] astfel ca trebuie sa fiti atenti cand scrieti astfel de cod. Luati in considerare si folosirea de nume mai sugestive pentru variabile.

• Cheatsheet vectori
• Wikipedia - Căutare binară
• Wikipedia - Algoritmi de sortare
• Wikipedia - Matrix Multiplication
• GDB - Tutorial