This is an old revision of the document!

Laborator 06: Minimax

Responsabili:

Obiective laborator

Insusirea unor cunostinte de baza despre teoria jocurilor precum si despre jocurile de tip joc de suma zero (suma nula, zero-sum games)
Insusirea abilitatii de rezolvare a problemelor ce presupun cunoasterea si exploatarea conceptului de joc de suma zero (zero-sum game);
Insusirea unor cunostinte elementare despre algoritmii necesari rezolvarii unor probleme de joc de suma zero (zero-sum game).

Precizari initiale

Un curs foarte bine explicat este pe canalul de YouTube de la MIT. Va sfatuim sa vizionati integral Search: Games, Minimax, and Alpha-Beta inainte sa parcurgeti materialul de pe ocw.

Importanţă – aplicaţii practice

Algoritmul Minimax si variantele sale imbunatatite (Negamax, Alpha-Beta etc.) sunt folosite in diverse domenii precum teoria jocurilor (Game Theory), teoria jocurilor combinatorice (Combinatorial Game Theory – CGT), teoria deciziei (Decision Theory) si statistica.

Astfel, diferite variante ale algoritmului sunt necesare in proiectarea si implementarea de aplicatii legate de inteligenta artificiala, economie, dar si in domenii precum stiinte politice sau biologie.

Descrierea problemei și a rezolvărilor

Algoritmii Minimax permit abordarea unor probleme ce tin de teoria jocurilor combinatorice. CGT este o ramura a matematicii ce se ocupa cu studierea jocurilor in doi (two-player games), in care participantii isi modifica rand pe rand pozitiile in diferite moduri, prestabilite de regulile jocului, pentru a indeplini una sau mai multe conditii de castig.

Exemple de astfel de jocuri sunt: sah, go, dame (checkers), X si O (tic-tac-toe) etc.

CGT nu studiaza jocuri ce presupun implicarea unui element aleator (sansa) in derularea jocului precum poker, blackjack, zaruri etc. Astfel decizia abordarii unor probleme rezolvabile prin metode de tip Minimax se datoreaza in principal simplitatii atat conceptuale, cat si raportat la implementarea propriu-zisa.

Minimax

Strategia pe care se bazeaza ideea algoritmului este ca jucatorii implicati adopta urmatoarele strategii:

Jucatorul 1 (maxi) va incerca mereu sa-si maximizeze propriul castig prin mutarea pe care o are de facut;
Jucatorul 2 (mini) va incerca mereu sa minimizeze castigul jucatorului 1 la fiecare mutare.

De ce merge o astfel de abordare? Dupa cum se preciza la inceput, discutia se axeaza pe jocuri de suma zero (zero-sum game). Acest lucru garanteaza, printre altele, ca orice castig al Jucatorului 1 este egal cu modulul sumei pierdute de Jucatorul 2. Cu alte cuvinte cat pierde Jucator 2, atat castiga Jucator 1. Invers, cat pierde Jucator 1, atat castiga Jucator 2. Sau

$$Win_{Player_1} = | Loss_{Player_2} |$$ $$| Loss_{Player_1} | = Win_{Player_2}$$

Reprezentarea spatiului solutiilor

In general spatiul solutiilor pentru un joc in doi de tip zero-sum se reprezinta ca un arbore, fiecarui nod fiindu-i asociata o stare a jocului in desfasurare (game state). Pentru exemplul nostru de X si O putem considera urmatorul arbore ( partial ) de solutii, ce corespunde primelor mutari ale lui X, respectiv O:

Metodele de reprezentare a arborelui variaza in functie de paradigma de programare aleasa, de limbaj, precum si de gradul de optimizare avut in vedere.

Avand notiunile de baza asupra strategiei celor doi jucatori, precum si a reprezentarii spatiului solutiilor problemei, putem formula o prima varianta a algoritmului Minimax:

Pseudocod Minimax

int evaluate(stare);   // functia returneaza un scor asociat cu starea
                       // functia returneaza mereu scorul din perspectiva lui maxi
 
 
void apply_move(move); // functia modifica starea curenta: executa miscarea move
void undo_move(move);  // functia restaureaza starea anterioara (de dinainte de executa lui move)
 
// alege cea mai buna mutare pentru jucatorul maxi
// functia returneaza best_score pentru maxi
int maxi(int depth) {
    // daca jocul s-a terminat sau am atins nivelul maxim de recursivitate ales
    if (gameOver() || depth == 0 ) {
        return evaluate();            // ne oprim si evaluam starea curenta
    }
 
    int max = -oo;                    // jucatorul maxi doreste sa-si maximizeze 
 
    // incercam pe rand fiecare care miscare posibila move   
    for (move : all_moves) {
        apply_move(move);         // executa move
 
        // incercam sa simulam jocul mai departe: 
        // daca maxi face move, ce ar face mini?
        int score = mini(depth - 1);
 
        // dintre toate variantele pe care mini le permite (!!!),
        // maxi o va alege pe cea cu scor maxim
        if (score > max) {
            max = score;
        }
 
        undo_move(move);         // restaureaza starea de dinainte de move
    }
 
    // cel mai bun scor pe care il poate obtine maxi este max
    // (s-a tinut cont si de ce i-ar permite mini, avand in vedere ca si el joaca optim)
    return max;
}
 
// alege cea mai buna mutare pentru jucatorul mini
// functia returneaza best_score pentru mini
int mini(int depth) {
    // daca jocul s-a terminat sau am atins nivelul maxim de recursivitate ales
    if (gameOver() || depth == 0 ) {
        return -evaluate();            // ne oprim si evaluam starea curenta
    }
 
    int min = +oo;                    // jucatorul mini doreste sa minimizeze scorul lui maxi 
 
    // incercam pe rand fiecare care miscare posibila move   
    for (move : all_moves) {
        apply_move(move);         // executa move
 
        // incercam sa simulam jocul mai departe: 
        // daca mini face move, ce ar face maxi?
        int score = maxi(depth - 1);
 
        // dintre toate variantele pe care maxi le permite (!!!),
        // mini o va alege pe cea cu scor minim
        if (score < min) {
            min = score;
        }
 
        undo_move(move);         // este o functie care incearca sa refaca
                                 // starea de dinainte de aplicarea lui move
    }
 
    // cel mai bun scor pe care il poate obtine mini este min
    // (s-a tinut cont si de ce i-ar permite maxi, avand in vedere ca si el joaca optim)
    return min;
}

Argumentarea utilizarii unei adancimi maxime

Datorita spatiului de solutii mare, de multe ori coplesitor ca volum, o inspectare completa a acestuia nu este fezabila si devine impracticabila din punctul de vedere al timpului consumat sau chiar a memoriei alocate (se vor discuta aceste aspecte in paragraful legat de complexitate).

Astfel, de cele mai multe ori este preferata o abordare care parcurge arborele numai pana la o anumita adancime maxima („depth”). Aceasta abordare permite examinarea arborelui destul de mult pentru a putea lua decizii minimalist coerente in desfasurarea jocului.

Totusi, dezavantajul major este ca pe termen lung se poate dovedi ca decizia luata la adancimea depth nu este global favorabila jucatorului in cauza.

De asemenea, se observa recursivitatea indirecta. Prin conventie acceptam ca inceputul algoritmului sa fie cu functia maxi. Astfel, se analizeaza succesiv diferite stari ale jocului din punctul de vedere al celor doi jucatori pana la adancimea depth. Rezultatul intors este scorul final al miscarii celei mai bune.

Negamax

Negamax este o varianta a minimax, ce se bazeaza pe urmatoarea observatie: intr-un joc cu suma zero castigul unui jucator este egal cu modulul sumei pierdute de celalalt jucator si invers.

Intr-adevar putem spune ca jucatorul mini incearca de fapt sa maximizeze in modul suma pierduta de maxi. Astfel putem formula urmatoarea implementare ce profita de observatia de mai sus.

Nota: putem exprima aceasta observatie si pe baza formulei max(a, b) = -min(-a, -b).

Pseudocod Negamax

int evaluate(stare);   // functia returneaza un scor asociat cu starea
                       // functia returneaza mereu scorul din perspectiva jucatorului CURENT!
 
 
void apply_move(move); // functia modifica starea curenta: executa miscarea move
void undo_move(move);  // functia restaureaza starea anterioara (de dinainte de executa lui move)
 
// alege cea mai buna mutare pentru jucatorul CURENT (EU)
// functia returneaza best_score
int negamax(int depth) {
    // daca jocul s-a terminat sau am atins nivelul maxim de recursivitate ales
    if (gameOver() || depth == 0 ) {
       return evaluate();            // ne oprim si evaluam starea curenta
    }
 
    int max = -oo;                    // jucatorul CURENT doreste sa-si  maximizeze scorul 
 
    // incercam pe rand fiecare care miscare posibila move   
    for (move : all_moves) {
        apply_move(move);         // executa move
 
        // incercam sa simulam jocul mai departe: 
        // daca jucatorul CURENT face face move, ce ar face ADVERSARUL?
        int score = -negamax(depth - 1);  // cel mai bine pentru el, 
                                          // este cel mai rau pentru mine si invers
 
        // dintre toate variantele pe care ADVERSARUL le permite (!!!),
        // EU (jucatorul CURENT) o voi alege pe cea cu scor maxim
        if (score > max) {
            max = score;
        }
 
        undo_move(move);         // restaureaza starea de dinainte de move
    }
 
    // cel mai bun scor pe care il pot obtine EU este max
    // (s-a tinut cont si de ce mi-ar permite ADVERSARUL, avand in vedere ca si el joaca optim)
    return max;
}

Se observa direct avantajele acestei formulari fata de Minimax-ul standard prezentat anterior:

claritatea si eleganta sporita a codului
usurinta in intretinerea si extinderea functionalitatii

Din punctul de vedere al complexitatii temporale, Negamax nu difera absolut deloc de Minimax (ambele examineaza acelasi numar de stari in arborele de solutii).

Putem concluziona ca este de preferat o implementare ce foloseste negamax fata de una bazata pe minimax in rezolvarea unor probleme ce tin de aceasta tehnica.

Alpha-beta pruning

Pana acum s-a discutat despre algoritmii Minimax / Negamax. Acestia sunt algoritmi exhaustivi (exhausting search algorithms). Cu alte cuvinte, ei gasesc solutia optima examinand intreg spatiul de solutii al problemei. Acest mod de abordare este extrem de ineficient in ceea ce priveste efortul de calcul necesar, mai ales considerand ca extrem de multe stari de joc inutile sunt explorate (este vorba de acele stari care nu pot fi atinse datorita incalcarii principiului de maximizare a castigului la fiecare runda).

O imbunatatire substantiala a minimax/negamax este Alpha-beta pruning (taiere alfa-beta). Acest algoritm incearca sa optimizeze mini/negamax profitand de o observatie importanta: pe parcursul examinarii arborelui de solutii se pot elimina intregi subarbori, corespunzatori unei miscari m, daca pe parcursul analizei gasim ca miscarea m este mai slaba calitativ decat cea mai buna miscare curenta.

Astfel, consideram ca pornim cu o prima miscare M1. Dupa ce analizam aceasta miscare in totalitate si ii atribuim un scor, continuam sa analizam miscarea M2. Daca in analiza ulterioara gasim ca adversarul are cel putin o miscare care transforma M2 intr-o miscare mai slaba decat M1 atunci orice alte variante ce corespund miscarii M2 (subarbori) nu mai trebuie analizate.

De ce?

De ce? Pentru ca stim ca exista cel putin o varianta in care adversarul obtine un castig mai bun decat daca am fi jucat miscarea M1.

Nu conteaza exact cat de slaba poate fi miscarea M2 fata de M1. O analiza amanuntita ar putea releva ca poate fi si mai slaba decat am constatat initial, insa acest lucru este irelevant.

De ce insa ignoram intregi subarbori si miscari potential bune numai pentru o miscare slaba gasita? Pentru ca, in conformitate cu principiul de maximizare al castigului folosit de fiecare jucator, adversarul va alege exact acea miscare ce ii va da un castig maximal. Daca exista o varianta si mai buna pentru el este irelevant, deoarece noi suntem interesati daca cea mai slaba miscare buna a lui este mai buna decat miscarea noastra curent analizata.

O observatie foarte importanta se poate face analizand modul de functionare al acestui algoritm: este extrem de importanta ordonarea miscarilor dupa valoarea castigului.

In cazul ideal in care cea mai buna miscare a jucatorului curent este analizata prima, toate celelalte miscari, fiind mai slabe, vor fi eliminate din cautare timpuriu.

In cazul cel mai defavorabil insa, in care miscarile sunt ordonate crescator dupa castigul furnizat, Alpha-beta are aceeasi compelxitate cu Mini/Nega-max, neobtinandu-se nicio imbunatatire.

In medie se constata o imbunatatire vizibila a algoritmului Alpha-beta fata de Mini/Nega-max.

Exemplu Grafic

Rolul miscarilor analizate la inceput presupune stabilirea unor plafoane de minim si maxim legate de cat de bune/slabe pot fi miscarile.

Astfel, plafonul de minim (Lower Bound), numit alpha stabileste ca o miscare nu poate fi mai slaba decat valoarea acestui plafon. Plafonul de maxim (Upper Bound), numit beta, este important doarece el foloseste la a stabili daca o miscare este prea buna pentru a fi luata in considerare. Depasirea plafonului de maxim inseamna ca o miscare este atat de buna incat adversarul nu ar fi permis-o, adica mai sus in arbore exista o miscare pe care ar fi putut s-o joace pentru a nu ajunge in situatia curent analizata.

Astfel alpha si beta furnizeaza o fereastra folosita pentru a filtra miscarile posibile pentru cei doi jucatori. Evident aceasta fereastra se poate actualiza pe masura ce se analizeaza mai multe miscari. De exemplul plafonul minim alpha se mareste pe masura ce gasim anumite tipuri de miscari mai bune (better worst best moves). Asadar, in implementare tinem seama si de aceste doua plafoane. In conformitate cu principiul Minimax, plafonul de minim al unui jocator (alpha-ul) este plafonul de maxim al celuilalt (beta-ul) si invers. Prezentam in continuare o descriere grafica a algoritmului Alpha-beta:

Un video cu un exemplu detaliat si foarte bine explicat se gaseste in tutorialul recomandat de pe YouTube (de la minutul 21:30 la 30:30).

Implementare

In continuare prezentam o implementare conceptuala a Alpha-beta, atat pentru Minimax, cat si pentru Negamax:

Pseudocod Minimax with Alpha-beta

int evaluate(stare);   // functia returneaza un scor asociat cu starea
                       // functia returneaza mereu scorul din perspectiva lui maxi
 
 
void apply_move(move); // functia modifica starea curenta: executa miscarea move
void undo_move(move);  // functia restaureaza starea anterioara (de dinainte de executa lui move)
 
// alege cea mai buna mutare pentru jucatorul maxi
// functia returneaza best_score pentru maxi, dar tine cont si de ce ii perminte mini
int aplhabeta_maxi(int aplha, int beta, int depth) {
    // daca jocul s-a terminat sau am atins nivelul maxim de recursivitate ales
    if (gameOver() || depth == 0 ) {
        return evaluate();            // ne oprim si evaluam starea curenta
    }
 
    // incercam pe rand fiecare miscare posibila move   
    for (move : all_moves) {
	apply_move(move);         // executa move
 
        // incercam sa simulam jocul mai departe: 
        // daca maxi face move, ce ar face mini?
        int score = alphabeta_mini(alpha, beta, depth - 1);
 
        if (score >= beta) {
            return beta;    // beta cut-off
        }
 
        // dintre toate variantele pe care mini le permite (!!!),
        // maxi o va alege pe cea cu scor maxim
        if (score > alpha) {
            alpha = score;
        }
 
        undo_move(move);         // restaureaza starea de dinainte de move
   }
 
    // cel mai bun scor pe care il poate obtine maxi este alpha
    // (s-a tinut cont si de ce i-ar permite mini, avand in vedere ca si el joaca optim)
    return alpha;
}
 
 
// alege cea mai buna mutare pentru jucatorul mini
// functia returneaza best_score pentru mini, dar tine cont si de ce ii perminte maxi
int aplhabeta_mini(int aplha, int beta, int depth) {
    // daca jocul s-a terminat sau am atins nivelul maxim de recursivitate ales
    if (gameOver() || depth == 0 ) {
        return -evaluate();            // ne oprim si evaluam starea curenta
    }
 
    // incercam pe rand fiecare miscare posibila move   
    for (move : all_moves) {
        apply_move(move);         // executa move
 
        // incercam sa simulam jocul mai departe: 
        // daca mini face move, ce ar face maxi?
        int score = alphabeta_maxi(alpha, beta, depth - 1);
 
        if (score <= alpha) {
            return alpha;    // alpha cut-off
        }
 
        // dintre toate variantele pe care maxi le permite (!!!),
        // mini o va alege pe cea cu scor minim
        if (score < beta) {
            beta = score;
        }
 
        undo_move(move);         // restaureaza starea de dinainte de move
    }
 
    // cel mai bun scor pe care il poate obtine mini este beta
    // (s-a tinut cont si de ce i-ar permite maxi, avand in vedere ca si el joaca optim)
    return beta;
}

Pseudocod Negamax with Alpha-beta

int evaluate(stare);   // functia returneaza un scor asociat cu starea
                       // functia returneaza mereu scorul din perspectiva jucatorului CURENT!
 
 
void apply_move(move); // functia modifica starea curenta: executa miscarea move
void undo_move(move);  // functia restaureaza starea anterioara (de dinainte de executa lui move)
 
// alege cea mai buna mutare pentru jucatorul CURENT (EU)
// functia returneaza best_score
int alphabeta_negamax(int aplha, int beta, int depth) {
    // daca jocul s-a terminat sau am atins nivelul maxim de recursivitate ales
    if (gameOver() || depth == 0 ) {
       return evaluate();            // ne oprim si evaluam starea curenta
    }
 
    // incercam pe rand fiecare care miscare posibila move   
    for (move : all_moves) {
        apply_move(move);         // executa move
 
        // incercam sa simulam jocul mai departe: 
        // daca jucatorul CURENT face face move, ce ar face ADVERSARUL?
        int score = -alphabeta_negamax(-beta, -aplha depth - 1);  // cel mai bine pentru el, 
                                                                  // este cel mai rau pentru mine
                                                                  // si invers
 
        // dintre toate variantele pe care ADVERSARUL le permite (!!!),
        // EU (jucatorul CURENT) o voi alege pe cea cu scor maxim
        if (score >= alpha) {
            alpha = score;
        }
 
        if (alpha >= beta) {
            break;               // cut-off
        }
 
        undo_move(move);         // restaureaza starea de dinainte de move
    }
 
    // cel mai bun scor pe care il pot obtine EU este alpha
    // (s-a tinut cont si de ce mi-ar permite ADVERSARUL, avand in vedere ca si el joaca optim)
    return alpha;
}

Din nou remarcam claritatea si coerenta sporita a variantei negamax!

Complexitate

In continuare prezentam complexitatile asociate algoritmilor prezentati anterior. Pentru aceasta vom introduce cateva notiuni:

branch factor : b = numarul mediu de ramificari pe care le are un nod neterminal (care nu e frunza) din arborele de solutii
depth : d = adancimea maxima pana la care se face cautarea in arborele de solutii
- orice nod de adancime d va fi considerat terminal

Un arbore cu un branching factor b, care va fi examinat pana la un nivel d va furniza $b^d$ noduri frunze ce vor trebui procesate (ex. calculam scorul pentru acele noduri).

Explicatie

Nivelurile sunt notate cu $0, 1, 2, ..., d$

nivel 0: $1$ nod (radacina)
nivel 1: $b$ noduri
nivel 2: $b^2$ noduri
nivel 3: $b^3$ noduri
…
nivel d: $b^d$ noduri

minimax/negamax
- Un algoritm mini/negamax clasic, care analizeaza toate starile posibile, va avea complexitatea $O(b ^ d)$ - deci exponentiala.

alpha-beta
- Cat de bun este insa alpha-beta fata de un mini/nega-max naiv? Dupa cum s-a mentionat anterior, in functie de ordonarea miscarilor ce vor fi evaluate putem avea un caz cel mai favorabil si un caz cel mai defavorabil.
- best case : miscarile sunt ordonate descrescator dupa castig (deci ordonate optim), rezulta o complexitate
  - $O(b*1*b*1*b*1...de\ d \ ori...b*1)$ pentru d par
  - $O(b*1*b*1*b*1...de \ d \ ori...b)$ pentru d impar
  - restrangand ambele expresii rezulta o complexitate $O(b ^ {\frac{d}{2}}) = O(\sqrt{b^d})$
  - prin urmare, intr-un caz ideal, algoritmul alpha-beta poate explora de 2 ori mai putine nivele in arborele de solutii fata de un algoritm mini/nega-max naiv.
- worst case: miscarile sunt ordonate crescator dupa castigul furnizat unui jucator, astfel fiind necesara o examinare a tuturor nodurilor pentru gasirea celei mai bune miscari.
  - in consecinta complexitatea devine egala cu cea a unui algoritm mini/negamax naiv.

Concluzii si observatii

Alpha-beta NU ofera o alta solutie fata de Minimax! Este doar o optimizare pusa deasupra algoritmului Minimax care ne permite sa exploram mai multe stari in acelasi timp sau pentru acelasi numar de stari sa optinem un timp de doua ori mai mic.

Exemple

Dintre cele mai importante jocuri in care putem aplica direct strategia minimax, mentionam:

X și 0
- joc foarte simplu/usor (spatiul starilor este mic).
- Prin urmare tot arborele de solutii poate fi generat si explorat intr-un timp foarte scurt.
sah
- joc foarte greu (spatiul starilor este foarte mare)
- minimax/negamax simplu poate merge pana la $ d = 7$ (nu reusea da bata campionul mondial la sah - campion uman)
- alpha-beta poate merge pana la $d = 14$
- Deep Blue a fost implementarea unui bot cu minimax si alpha-beta care a batut in 1997 campionul mondial la sah (Gary Kasparov).
Ultimate tic-tac-toe
- varianta mult mai grea de X si 0 (spatiul starilor foarte mare)
- s-a dat la proiect PA 2016 :D
- implemantarile se pot testa aici
Nim
Reversi

Alte exempe de jocuri interesante:

Go
- solutiile se bazeaza pe Monte Carlo Tree Search (nu pe minimax)
- AlphaGo este botul cel mai bun pe tabla de 19×19

Nim

Fiind date 3 multimi de bile, fiecare jucator trebuie sa extraga la fiecare mutare 1, 2 sau 3 bile din oricare multime.

Cel care este fortat sa aleaga ultima bila, pierde.

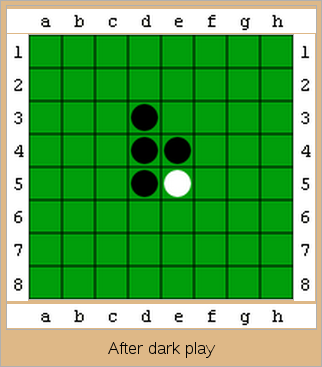
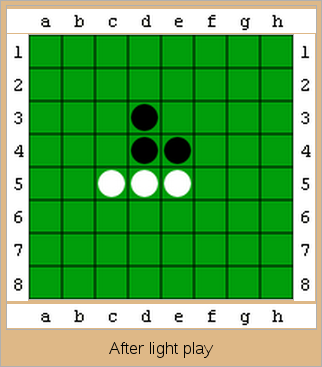
Reversi game

Tabla de joc consista dintr-un grid 6×6. Piesele pot fi reprezentate de monede, fiecarui jucator fiindu-i asociata o fata diferita a monezii. Jucatorii muta alternativ, dupa regula urmatoare:

Pozitia (x, y) in care este plasata piesa trebuie sa fie libera
Trebuie sa existe o alta pozitie (x', y'), pe aceeasi linie, coloana sau diagonala a jucatorului aflat la mutare si toate pozitiile dintre (x, y) si (x', y') trebuie sa fie ocupate de piese ale adversarului
Piesele adversarului dintre (x, y) si (x', y') vor fi capturate, intorcandu-se monedele pe cealalta fata.

Mai jos, de la stanga spre dreapta: pozitia initiala, posibilitatile de mutare ale primului jucator, tabla dupa prima mutare, posibilitatile de mutare ale celuilalt jucator, tabla dupa a doua mutare.

Observatii:

Jucatorul poate acapara piese ale adversarului in mai multe directii simultan
Daca un jucator nu are unde muta, acesta cedeaza randul, adversarul efectuand a doua mutare la rand
Jocul se incheie cand nimeni nu mai poate muta, invingatorul fiind acela care detine cele mai multe piese proprii

Exercitii

In acest laborator vom folosi scheletul de laborator din arhiva skel-lab06.zip.

Vom implementa algoritmi pentru jocurile Nim si Reversi.

Minimax Nim

Se doreste implementarea algoritmulului minimax sau negamax pentru Nim.

Recomandam implementarea variantei Negamax.

Minimax Reversi

Se doreste implementarea algoritmulului minimax sau negamax pentru Reversi.

Recomandam implementarea variantei Negamax.

Bonus

Extindeti algoritmul implementat anterior pentru jocul Reversi intr-un algoritm de tip alpha-beta pruning. Cum puteti sa comparati cei doi algoritmi implementati pentru Reversi?