This is an old revision of the document!

Lab 03

Exercise 1

Advantage. The purpose of this problem is to clarify the concept of advantage. Con- sider the following two experiments EXP(0) and EXP(1):

In EXP(0) the challenger flips a fair coin (probability 1/2 for HEADS and 1/2 for TAILS) and sends the result to the adversary A.
In EXP(1) the challenger always sends TAILS to the adversary.

The adversary’s goal is to distinguish these two experiments: at the end of each experiment the adversary outputs a bit 0 or 1 for its guess for which experiment it is in. For b = 0,1 let Wb be the event that in experiment b the adversary output 1. The adversary tries to maximize its distinguishing advantage, namely the quantity Adv = | Pr[W0] − Pr[W1] | ∈ [0, 1] .

The advantage Adv captures the adversary’s ability to distinguish the two experiments. If the advantage is 0 then the adversary behaves exactly the same in both experiments and therefore does not distinguish between them. If the advantage is 1 then the adversary can tell perfectly what experiment it is in. If the advantage is negligible for all efficient adversaries (as defined in class) then we say that the two experiments are indistinguishable.

a. Calculate the advantage of each of the following adversaries:

A1: Always output 1.
A2: Ignore the result reported by the challenger, and randomly output 0 or 1 with even probability.
A3: Output 1 if HEADS was received from the challenger, else output 0.
A4: Output 0 if HEADS was received from the challenger, else output 1.
A5: If HEADS was received, output 1. If TAILS was received, randomly output 0 or 1 with even probability.

b. What is the maximum advantage possible in distinguishing these two experiments? Explain why.

Exercise 2

Let's use the experiment defined earlier as a pseudorandom generator (PRG) as follows:

Set a desired output length n
Obtain a random sequence R of bits of length n (say flipping a coin, using a Linear-congruential generator, or any other method)
For each bit r in the random sequence R generated in the previous step, output a bit b as follows:

if the bit r is 0, then output a random bit b (e.g. flip a coin and output either 0 or 1 depending on its result)
if the bit r is 1, then output 1

a. Implement the frequency (monobit) test from NIST (see section 2.1): http://csrc.nist.gov/publications/nistpubs/800-22-rev1a/SP800-22rev1a.pdf

and check if a sequence generated by the above PRG (say n=100) seems random or not.

b. Run the test on a random bitstring (e.g. a string such as R used by the above PRG), and compare the result of the test.

If the two results are different across many iterations, this test already gives you an attacker that breaks the PRG.

You may use a function like this to generate a random bitstring

import random

def get_random_string(n): #generate random bit string
  bstr = bin(random.getrandbits(n)).lstrip('0b').zfill(n)
  return bstr

Also, in Python you may find the functions sqrt, fabs and erfc from the module math useful

…………

In this lab we shall do some exercises related to PRFs, PRPs and DES. Please check the course, available here: http://cs.curs.pub.ro/2014/pluginfile.php/13095/mod_resource/content/1/sasc_curs4.pdf

Exercise 1

Let F : K × X → Y be a secure PRF with K = X = Y = {0, 1}ⁿ.

a) Show that F1(k,x) = F(k,x) || 0 is not a secure PRF. (for strings y and z we use y || z to denote the concatenation of y and z)
b) Prove that F2(k, x) = F (k, x ⊕ 1ⁿ) is a secure PRF. Here x ⊕ 1ⁿ is the bit-wise complement of x. To prove security argue the contra-positive: a distinguisher A that breaks F2 implies a distinguisher B that breaks F and whose running time is about the same as A’s.
c) Let K3 = {0, 1}ⁿ⁺¹. Construct a new PRF F3 : K3 ×X → Y with the following property: the PRF F3 is secure, however if the adversary learns the last bit of the key then the PRF is no longer secure. This shows that leaking even a single bit of the secret key can completely destroy the PRF security property.

Hint: Let k3 = k || b where k ∈ {0,1}ⁿ and b ∈ {0,1}. Set F3(k3,x) to be the same as F (k, x) for all x != 0ⁿ. Define F3(k3, 0ⁿ) so that F3 is a secure PRF, but becomes easily distinguishable from a random function if the last bit of the secret key k3 is known to the adversary. Prove that your F3 is a secure PRF by arguing the contra-positive, as in part (b).

d) Construct a new PRF F4 : K2 × X → Y that remains secure if the attacker learns any single bit of the key. Your function F2 may only call F once. Briefly explain why your PRF remains secure if any single bit of the key is leaked.

Exercise 2

Let's analyse some substitution-permutation networks (SPN).

SPN 1

We have the SPN from this figure:

where S denotes the AES S-box (we'll discuss this in some detail during the next lecture), and 'Permutation' is a simple permutation block that simply shifts the input 4 bits to the right as in a queue. Both this S-box and the permutation are invertible and known by the attacker (you). Each input (x1, x2) is 8-bit (1 byte), as well as the keys k1, k2, and the outputs y1, y2.

How can you find the key ?
Given the message/ciphertext pair ('Hi' - as characters, 0xba52 - as hex number), find the key bytes k1 and k2. Print them in ascii.

For these exercises you can use the following helper/starter code:

import sys
import random
import string
import operator

# Rijndael S-box
sbox =  [0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67,
        0x2b, 0xfe, 0xd7, 0xab, 0x76, 0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59,
        0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0, 0xb7,
        0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1,
        0x71, 0xd8, 0x31, 0x15, 0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05,
        0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75, 0x09, 0x83,
        0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29,
        0xe3, 0x2f, 0x84, 0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b,
        0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf, 0xd0, 0xef, 0xaa,
        0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c,
        0x9f, 0xa8, 0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc,
        0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2, 0xcd, 0x0c, 0x13, 0xec,
        0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19,
        0x73, 0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee,
        0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb, 0xe0, 0x32, 0x3a, 0x0a, 0x49,
        0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79,
        0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4,
        0xea, 0x65, 0x7a, 0xae, 0x08, 0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6,
        0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a, 0x70,
        0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9,
        0x86, 0xc1, 0x1d, 0x9e, 0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e,
        0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf, 0x8c, 0xa1,
        0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0,
        0x54, 0xbb, 0x16]


# Rijndael Inverted S-box
rsbox = [0x52, 0x09, 0x6a, 0xd5, 0x30, 0x36, 0xa5, 0x38, 0xbf, 0x40, 0xa3,
        0x9e, 0x81, 0xf3, 0xd7, 0xfb , 0x7c, 0xe3, 0x39, 0x82, 0x9b, 0x2f,
        0xff, 0x87, 0x34, 0x8e, 0x43, 0x44, 0xc4, 0xde, 0xe9, 0xcb , 0x54,
        0x7b, 0x94, 0x32, 0xa6, 0xc2, 0x23, 0x3d, 0xee, 0x4c, 0x95, 0x0b,
        0x42, 0xfa, 0xc3, 0x4e , 0x08, 0x2e, 0xa1, 0x66, 0x28, 0xd9, 0x24,
        0xb2, 0x76, 0x5b, 0xa2, 0x49, 0x6d, 0x8b, 0xd1, 0x25 , 0x72, 0xf8,
        0xf6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xd4, 0xa4, 0x5c, 0xcc, 0x5d,
        0x65, 0xb6, 0x92 , 0x6c, 0x70, 0x48, 0x50, 0xfd, 0xed, 0xb9, 0xda,
        0x5e, 0x15, 0x46, 0x57, 0xa7, 0x8d, 0x9d, 0x84 , 0x90, 0xd8, 0xab,
        0x00, 0x8c, 0xbc, 0xd3, 0x0a, 0xf7, 0xe4, 0x58, 0x05, 0xb8, 0xb3,
        0x45, 0x06 , 0xd0, 0x2c, 0x1e, 0x8f, 0xca, 0x3f, 0x0f, 0x02, 0xc1,
        0xaf, 0xbd, 0x03, 0x01, 0x13, 0x8a, 0x6b , 0x3a, 0x91, 0x11, 0x41,
        0x4f, 0x67, 0xdc, 0xea, 0x97, 0xf2, 0xcf, 0xce, 0xf0, 0xb4, 0xe6,
        0x73 , 0x96, 0xac, 0x74, 0x22, 0xe7, 0xad, 0x35, 0x85, 0xe2, 0xf9,
        0x37, 0xe8, 0x1c, 0x75, 0xdf, 0x6e , 0x47, 0xf1, 0x1a, 0x71, 0x1d,
        0x29, 0xc5, 0x89, 0x6f, 0xb7, 0x62, 0x0e, 0xaa, 0x18, 0xbe, 0x1b ,
        0xfc, 0x56, 0x3e, 0x4b, 0xc6, 0xd2, 0x79, 0x20, 0x9a, 0xdb, 0xc0,
        0xfe, 0x78, 0xcd, 0x5a, 0xf4 , 0x1f, 0xdd, 0xa8, 0x33, 0x88, 0x07,
        0xc7, 0x31, 0xb1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xec, 0x5f , 0x60,
        0x51, 0x7f, 0xa9, 0x19, 0xb5, 0x4a, 0x0d, 0x2d, 0xe5, 0x7a, 0x9f,
        0x93, 0xc9, 0x9c, 0xef , 0xa0, 0xe0, 0x3b, 0x4d, 0xae, 0x2a, 0xf5,
        0xb0, 0xc8, 0xeb, 0xbb, 0x3c, 0x83, 0x53, 0x99, 0x61 , 0x17, 0x2b,
        0x04, 0x7e, 0xba, 0x77, 0xd6, 0x26, 0xe1, 0x69, 0x14, 0x63, 0x55,
        0x21, 0x0c, 0x7d]

def strxor(a, b): # xor two strings (trims the longer input)
  return "".join([chr(ord(x) ^ ord(y)) for (x, y) in zip(a, b)])

def hexxor(a, b): # xor two hex strings (trims the longer input)
  ha = a.decode('hex')
  hb = b.decode('hex')
  return "".join([chr(ord(x) ^ ord(y)).encode('hex') for (x, y) in zip(ha, hb)])

def bitxor(a, b): # xor two bit strings (trims the longer input)
  return "".join([str(int(x)^int(y)) for (x, y) in zip(a, b)])
  
def str2bin(ss):
  """
    Transform a string (e.g. 'Hello') into a string of bits
  """
  bs = ''
  for c in ss:
    bs = bs + bin(ord(c))[2:].zfill(8)
  return bs

def hex2bin(hs):
  """
    Transform a hex string (e.g. 'a2') into a string of bits (e.g.10100010)
  """
  bs = ''
  for c in hs:
    bs = bs + bin(int(c,16))[2:].zfill(4)
  return bs

def bin2hex(bs):
  """
    Transform a bit string into a hex string
  """
  return hex(int(bs,2))[2:]

def byte2bin(bval):
  """
    Transform a byte (8-bit) value into a bitstring
  """
  return bin(bval)[2:].zfill(8)


def permute4(s):
  """
    Perform a permutatation by shifting all bits 4 positions right.
    The input is assumed to be a 16-bit bitstring
  """
  ps = ''
  ps = ps + s[12:16]
  ps = ps + s[0:12]
  return ps

def permute_inv4(s):
  """
    Perform the inverse of permute4
    The input is assumed to be a 16-bit bitstring
  """
  ps = ''
  ps = ps + s[4:16]
  ps = ps + s[0:4]
  return ps

def spn_1r_reduced_2s(k, x):
  """
    Performs an encryption with a substitution-permutation network.
    Key k = {k1, k2}, total of 16 bits (2 x 8 bits)
    Input x = {x1, x2}, total of 16 bits (2 x 8 bits)
    Both k and x are assumed to be bitstrings.

    Return:
    a 16-bit bitstring containing the encryption y = {y1, y2}
  """

  # Split input and key
  x1 = x[0:8]
  x2 = x[8:16]
  k1 = k[0:8]
  k2 = k[8:16]

  #Apply S-box
  u1 = bitxor(x1, k1)
  v1 = sbox[int(u1,2)]
  v1 = byte2bin(v1)

  u2 = bitxor(x2, k2)
  v2 = sbox[int(u2,2)]
  v2 = byte2bin(v2)

  #Apply permutation
  pin = v1 + v2
  pout = permute4(pin)

  return pout
  
def spn_1r_full_2s(k, x):
  """
    Performs an encryption with a substitution-permutation network.
    Key k = {k1, k2, k3, k4}, total of 32 bits (4 x 8 bits)
    Input x = {x1, x2}, total of 16 bits (2 x 8 bits)
    Both k and x are assumed to be bitstrings.

    Return:
    a 16-bit bitstring containing the encryption y = {y1, y2}
  """

  # Split input and key
  x1 = x[0:8]
  x2 = x[8:16]
  k1 = k[0:8]
  k2 = k[8:16]
  k3 = k[16:24]
  k4 = k[24:32]

  #Apply S-box
  u1 = bitxor(x1, k1)
  v1 = sbox[int(u1,2)]
  v1 = byte2bin(v1)

  u2 = bitxor(x2, k2)
  v2 = sbox[int(u2,2)]
  v2 = byte2bin(v2)

  #Apply permutation
  pin = v1 + v2
  pout = permute4(pin)

  #Apply final XOR
  po1 = pout[0:8]
  po2 = pout[8:16]
  y1 = bitxor(po1, k3)
  y2 = bitxor(po2, k4)

  return y1+y2
  
def main():

  #Run reduced 2-byte SPN
  msg = 'Hi'
  key = '??' # Find this
  xs = str2bin(msg)
  ks = str2bin(key)
  ys = spn_1r_reduced_2s(ks, xs)
  print 'Two y halves of reduced SPN: ' + ys[0:8] + ' (hex: ' + bin2hex(ys[0:8]) + '), ' + ys[8:16] + ' (hex: ' + bin2hex(ys[8:16]) + ')'

  #Run full 2-byte SPN
  msg = 'Om'
  key = '????' # Find this
  xs = str2bin(msg)
  ks = str2bin(key)
  ys = spn_1r_full_2s(ks, xs)
  print 'Two y halves of full SPN (2 bytes): ' + ys[0:8] + ' (hex: ' + bin2hex(ys[0:8]) + '), ' + ys[8:16] + ' (hex: ' + bin2hex(ys[8:16]) + ')'



if __name__ == "__main__":
  main()

SPN 2

Now we have a better SPN, where the output of the permutation is XOR-ed with another 2 key bytes, as in the following figure:

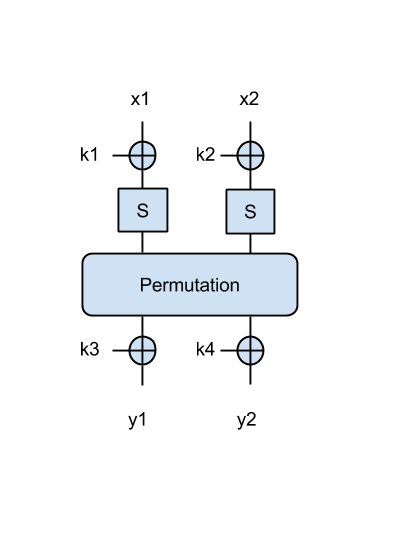
Try to find the key in this case, when given the following message/ciphertext pairs: ('Om', 0x0073), ('El', 0xd00e), ('an', 0x855b). Print the key in ascii.

You may try some kind of brute-force search

SPN 3

As another example, which uses a larger block size, let's use an SPN that takes a 4-byte input x=[x1 || x2 || x3 || x4] and an 8-byte key k=[k1 || k2 || k3 || k4 || k5 || k6 || k7 || k8] as in this figure:

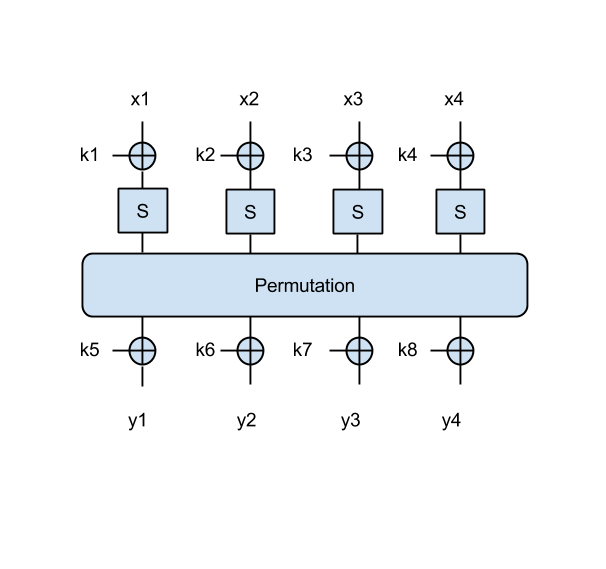
Note that in this 4-byte SPN, the permutation operates on all 4 bytes, similarly to the 2-byte SPN: that is, it shifts all bits four bits to the right.

Try to find the key in this case as well, using the following message/ciphertext pairs: ('Omul', 0xddcf7bc7), ('stea', 0x96d58b43), ('luna', 0x9c3f2303) . Again print the key in ascii.

This time you cannot (easily) do a brute-force on all the bytes of the last XOR. However, you may try to attack one S-box at a time. Think of the bits that affect one such S-box and find an efficient attack.