This is an old revision of the document!
Laboratorul 09
- Descărcați framwork-ul de laborator și copiați, din arhiva descărcată, directorul Lab9, în interiorul directorului gfx-framework-ppbg\src\lab din versiunea voastră de proiect.
- Adăugați în fișierul
lab_list.h, linia#include “lab/lab9/lab9.h”. - Folosiți din nou utilitarul CMake pentru a regenera proiectul. Pentru a vă reaminti procesul de realizare a setup-ului, puteți să reconsultați pagina dedicată acestui lucru.
Curbe de forma libera
Introducem conceptul de curba de forma libera pentru acele curbe ce nu pot fi definite analitic, printr-o formula inchisa. Exemple de curbe analitice sunt:
- Cercul - (x-a)^2 + (y-a)^2 = r
- Elipsa -
- …
Curbe Bézier
Prima curba de forma libera ce a fost definita, cronologic, este curba de baza descrisa mai jos ce a fost popularizata de catre Pierre Bézier in anii 60'. Aceasta este descrisa initial de catre Paul de Casteljau in obtinerea unui patent in 1959, dar este publicata abia in anii 80'. Cei doi autori au dezvoltat parametrizarea acestei forme independent.
Curba Bézier este o curba de aproximare ce contine un set de puncte ce controleaza forma curbei. Acest set poate contine orice numar de puncte. Formula pentru 2, 3 si 4 puncte de control arata in felul urmator:
Definitie recursiva
Formula curbei Bézier se poate defini recursiv dupa cum urmeaza:
$$ B_{n}(P_0, P_1,..., P_n, t) = (1-t) \cdot B_{n-1}(P_0, P_1,..., P_{n-1}, t) + t \cdot B_{n-1}(P_1, P_2,..., P_{n}, t) $$
Forma polinomiala
Forma polinomiala a curbei Bézier este dupa cum urmeaza:
$$ B(t) = \sum_{i=0}^{n}{\binom{n}{i} \cdot (1-t)^{n-i} \cdot t^i \cdot P_i}, \quad 0 \leq t \leq 1 $$
Pentru 4 puncte de control, forma curbei Bézier, pe baza definitiei de mai sus, arata in felul urmator:
$$ B(t) = (1-t)^3 \cdot P_0 + 3(1-t)^2 \cdot t \cdot P_1 + 3(1-t)^2 \cdot P_2 + t^3 \cdot P_3, \quad 0 \leq t \leq 1 $$
Polinomul urmator, utilizat in definitia formulei pentru curbele Bézier este cunoscut sub numele de polinom Bernstein, dupa numele lui Sergei Bernstein, ce a propus acest polinom in 1912:
$$ b_{i,n}(t) = \binom{n}{i} \cdot t^i \cdot (1-t)^{n-i}, \quad i=0,...,n $$
Suprafete generate
Definim o suprafata generata ca este acea suprafata creata printr-o metoda de multiplicare a unei geometrii suport. Crearea unei astfel de suprafete contine:
- Un generator, adică o geometrie definită explicit pe baza căreia are loc procesul de generare
- Un algoritm de generare. Acesta poate fi bazat pe rotație, translație sau pe orice fel de curbă definită prin puncte de control
Procesul de generare decurge astfel: întâi se desenează geometria generator, pe baza căreia este construită suprafața generată. După aceasta, se desenează un număr de instanțe ale geometriei generator, fiecare transformată de funcția de generare într-un mod progresiv. Rezultatul final este obținut prin combinarea topologică a acestor instanțe.
Suprafețe de translație
O suprafață de translație este o suprafață generată prin instanțierea unui obiect generator. Fiecare instanță a generatorului suferă o transformare de translație. O suprafață de translație poate fi definită prin instanțierea unui generator cu fiecare instanță translatată progresiv dupa o funcție.
Un exemplu de suprafață translatată este:

Suprafețe de rotație
O suprafață de rotație este o suprafață generată prin instanțierea unui obiect generator. Fiecare instanță a generatorului suferă o transformare de rotație. Aceasta poate fi definită prin instanțierea unui generator cu fiecare instanță rotită progresiv dupa o funcție.

Laborator
Instanțierea reprezintă un mecanism prin care se amplifică numărul de primitive trimise la banda grafică. Această amplificare este fie explicită (programată de utilizator în shader), fie implicită (generată prin comenzi OpenGL).
Pentru a instanția implict geometrie, există comanda:
glDrawElementsInstanced(topologie, nr_indecsi, tip_data, offset, instante).
De exemplu, dacă aș dori să desenez de 1540 de ori (instanțe) un obiect cu 99 de indecși, format din triunghiuri din buffer-ul de indecși, legat curent la banda grafică, atunci comanda ar fi:
glDrawElementsInstanced(GL_TRIANGLES, 99, GL_UNSIGNED_INT, 0, 1540);
Instanțierea explicită se face în shader, generând geometrie nouă prin comenzi glsl, în acest caz prin comenzi de geometry shader:
gl_Position = P*V*M*vec4(p1, 1); EmitVertex(); gl_Position = P*V*M*vec4(p2, 1); EmitVertex(); gl_Position = P*V*M*vec4(p3, 1); EmitVertex(); EndPrimitive();
Instanțirea oferă posibilitatea ușoară de a crește rapid numărul de obiecte din scenă, dacă obiectele sunt identice. Ex: copaci, tile-uri de teren, unități într-un rts, etc.
Pentru a lucra cu suprafețe de translație, rotație și/sau interpolare, vom folosi instanțiere. Totuși, chiar dacă avem N instanțe de geometrie generator, nu avem topologia necesară pentru a lega instanțele, deoarece generatorul este o curbă (topologie 2D), iar suprafața generată necesită topologie 3D.
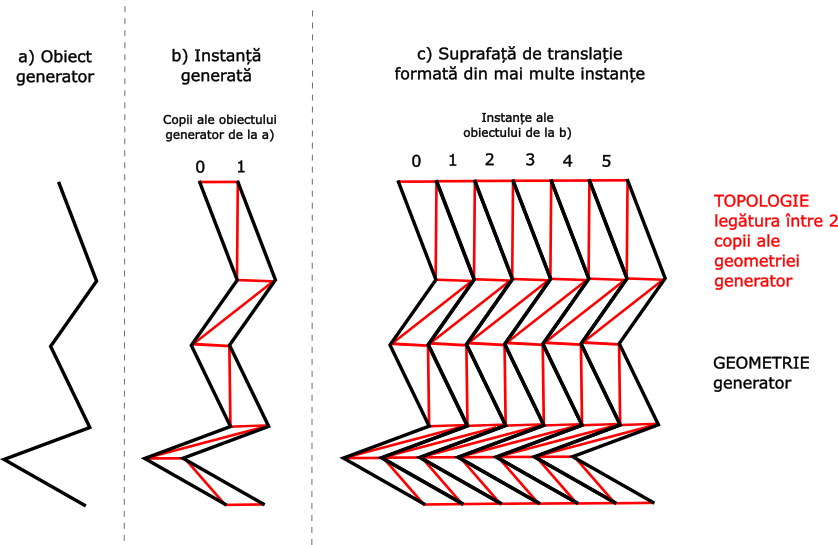
Din figură se observă clar cum avem mai multe tipuri de obiecte:
- Obiectul generator (prima linie neagră din stânga)
- Obiectul nou generat (2 instanțe ale generatorului și topologie de legatură între linii)
- Suprafața finală generată
Dacă nu am fi folosit acest proces, atunci prin instanțiere am fi obținut liniile instanțiate, dar nu și topologia de legatură între linii, adică exact ca în următoarea imagine:
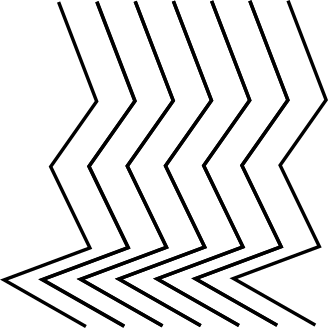
Cerinte laborator
- 0.1p - Modificati fisierul
GeometryShader.glslpentru a desena- Pe baza celor 4 puncte de control transmise, esantionati de mai multe ori curba bezier







