Table of Contents
a. Sumatoare multi-bit
În viața reală noi lucrăm cu numere reprezentabile pe mai mulți biți. Totuși, sumatoarele de tip Half-Adder și Full-Adder pot aduna cel mult un bit. Pentru depășirea acestei limitări, laboratorul trecut am implementat un circuit capabil să facă suma numerelor reprezentate pe mai mulți biți.
Sumatorul Ripple-Carry
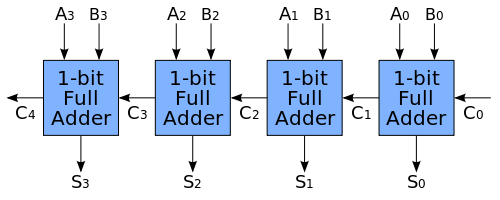
Cel mai simplu circuit este sumatorul ripple-carry care folosind N sumatoare full-adder poate însuma numere pe N biți.
Conectarea lor, prezentată în figura de mai sus, este una foarte simplă: ieșirea Cout a modulului de rang i va fi conectată la intrarea Cin a modulului de rang i+1.
Limitări
Implementarea acestuia este facilă, însă performanța este scăzută. De ce? Deoarece transportul de intrare pentru fiecare sumator complet este dependent de semnalul carry-out din full-adder-ul anterior. Prin structura sa internă: modulul de rang i trebuie să aştepte modulul de rang i-1 sa îşi termine execuția pentru a afla cât este Cin_i.
Îmbunătățiri
Cum putem implementa un circuit mai rapid? Eliminând dependența între rang-uri în ceea ce privește bitul de carry. Pentru început aflăm expresia în logică booleană pornind de la tabelul de adevăr al bitului de carry C1.
| A0 | B0 | C0 | C1 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Scriem expresia logică corespunzătoare liniilor din tabel pentru care C1 are valoarea 1:
- C1 = A0 * B0 * C0 + A0 * B0 * ~C0 + ~A0 * B0 * C0 + A0 * ~B0 * C0
- C1 = A0 * B0 * (C0 + ~C0) + C0 * (~A0 * B0 + A0 * ~B0)
- C1 = A0 * B0 + C0 * (A0 ⊕ B0)
Dacă generalizăm formula:
- Ci+1 = Ai * Bi + Ci * (Ai ⊕ Bi)
Prin urmare, pentru fiecare modul de full-adder, am putea calcula bitul carry de intrare cu cost constant egal cu 1, fără să mai așteptăm propagarea acestuia prin toate celelalte full-adder-e de rang mai mic.
- Cout = Generează_biții_carry? SAU Propagă_bitul_de_carry_de_la_rangul_inferior_dacă_nu_e_generat?