In the previous lecture we have investigated the semantics of regular expressions and saw that how we can determine the language accepted by, e.g. $ (A\cup B)(a\cup b)*(0 \cup 1)*$ . However, it is not straightforward to compute whether a given word $ w$ is a member of $ L(e)$ and this is precisely the task of the lexical stage.

In more formal terms, we have a generator - a means to construct a language from a regular expression, but we lack a means for accepting (words of) languages.

We shall informally illustrate an algorithm for verifying the membership $ w \in L((A\cup B)(a\cup b)*(0 \cup 1)*)$ , in Haskell:

check ('A':xs) = check1 xs
check ('B':xs) = check1 xs
check _ = False
 
check1 ('a':xs) = check1 xs
check1 ('b':xs) = check1 xs
check1 ('0':xs) = check2 xs
check1 ('1':xs) = check2 xs
check1 [] = True
check1 _ = False
 
check2 ('0':xs) = check2 xs
check2 ('1':xs) = check2 xs
check2 [] = True
check2 _ = False

The algorithm proceeds in three stages:

• in the first stage, we check if A or B are encountered, otherwise we move on to the second stage;
• in the second stage, we check if a, b, 0 or 1 are encountered; if a or b are found, we continue inspection in the second stage; if 0 or 1 are found, we continue inspection in the third stage; finally, if the string terminates, we report true;
• in the third stage we search for binary digits in a similar way;

The same strategy can be written in a more elegant way as:

check w = chk w++"!" [0]
   where chk (x:xs) set =
	| (x 'elem' ['A', 'B']) && (0 'elem' set) = chk xs [1,2,3]
	| (x 'elem' ['a', 'b']) && (1 'elem' set) = chk xs [1,2,3]
	| (x 'elem' ['0', '1']) && (2 'elem' set) = chk xs [2,3]
	| (x == '!') && (3 'elem' set) = True
	| otherwise = False

Here, we have introduced the symbol ! to mark the string termination, and thus make the whole code nicer to write. We have also made the stage idea explicit. The procedure chk maintains a set of stages or states:

• $ 0\in set$ indicates that we are in the initial stage, where we are looking for A or B
• $ 1\in set$ indicates that we have read a sequence of alphabetic symbols: as, bs may follow
• $ 2\in set$ indicates that the sequence of alphabetic symbols has ended; only 0s or 1s may follow;
• $ 3\in set$ indicates that the string may also terminate at any time - 3 is an end-stage.

We start in the initial stage. Whenever a symbol is read, the stage, i.e. the set of possible lookups is updated: for instance, when 0 or 1 are read, only the second and third situations are possible.

The idea behind our code could be expressed as the following diagram: where

• each node is a state, which indicates what is the current stage in the recognition of the input word;
• each arrow is a transition which takes the recognition process from one stage to another;
• here, $ Q_0$ is the initial state, $ Q'$ is the state from which any lower-case alphanumeric symbol in the alphabet may follow, and $ Q''$ is the state from which only numerics are accepted.

The string can terminate successfully in both $ Q$ and $ Q'$ , which is shown via double circles.

The key idea behind the previous algorithm can be generalised to any regular expression, and its associated code, written in the same style, yields a similar diagram.

In practice, it is the diagram, i.e. the nondeterministic finite automaton (NFA), which helps us generate the code.

Definition (NFA):

A non-deterministic finite automaton is a tuple $ M=(K,\Sigma,\Delta,q_0,F)$ where:

• $ K$ is a finite set of states
• $ \Sigma$ is an alphabet
• $ \Delta$ is a subset of $ K \times \Sigma^* \times K$ and is called a transition relation
• $ q_0\in K$ is the initial state
• $ F\subseteq K$ is the set of final states

As an example, consider:

• $ K=\{q_0,q_1,q_2\}$
• $ \Sigma=\{0,1\}$
• $ \Delta=\{(q_0,0,q_0),(q_0,1,q_0),(q_0,0,q_1),(q_1,1,q_2)\}$
• $ F = \{q_2\}$

Notice that the NFA gets stuck for certain inputs, i.e. it does not accept.

Graphical notation

Definition (Configuration):

A configuration of an NFA, is a member of $ K\times \Sigma^*$ .

Informally, configurations capture a snapshot of the execution of an NFA. The snapshot consists of the:

• current state of the automaton and
• the rest of the word from the input.

For instance, $ (q_0,0001)$ is the initial configuration of the automaton from our example, on input $ 0001$ .

Definition (Transition):

We call $ \vdash_M \subseteq (K\times \Sigma^*) \times (K\times\Sigma^*)$ a one-step move relation of automaton $ M$ . The relation describes how the automaton must behave to reach one configuration from another. Formally:

• $ (q,w) \vdash_M (q',w')$ if and only if there exists $ u\in\Sigma^*$ , such that $ w=uw'$ ($ u$ is a prefix of $ w$ ) and $ (q,u,q')\in\Delta$ : from state $ q$ on input $ u$ we reach state $ q'$ .

We call $ \vdash_M^*$ , the reflexive and transitive closure of $ \vdash_M$ , i.e. the zero-or-more step(s) move of automaton $ M$ .

For instance, in our previous example, $ (q_0,0001)\vdash_M(q_0,001)$ and also $ (q_0,0001)\vdash_M(q_1,001)$ . At the same time, $ (q_0,0001)\vdash_M^*(q_2,\epsilon)$ . Can you figure out the sequence of steps?

Proposition (Acceptance):

A word $ w$ is accepted by an NFA $ M$ iff $ (q_0,w)\vdash_M^*(q,\epsilon)$ and $ q\in F$ . In other words, after the word $ w$ was processed by the automaton, we reach a final state.

Notice that the word $ 0001$ is indeed accepted by the automaton $ M$ from our example.

Definition (Language accepted by an NFA):

Given an NFA $ M$ , we define $ L(M) = \{w\mid w\text{ is accepted by} M\}$ as the language accepted by $ M$ . We say $ M$ accepts the language $ L(M)$ .

Illustration of an AFN for $ (A\cup B)(a\cup b)*(0 \cup 1)*$ .

There are two ways of writing this automaton:

• one that follows exactly our previous algorithm sketch.
• one that employs epsilon transitions.

Epsilon transitions are a means for jumping from a state to another without consuming the input. It is a useful way of defining automata, because it empowers us to combine multiple automata procedures.

Notice that nondeterminism actually refers to our imperfect information regarding the current state of the automaton. Nondeterminism means that, after consuming some part (prefix) of a word, several concrete states may be possible current states.

While Regular Expressions are a natural instrument for declaring (or generating) tokens, NFAs are a natural instrument for accepting tokens (i.e. their respective language).

The following theorem shows how this can be achieved.

For every language $ L(E)$ defined by the regular expression $ E$ , there exists an NFA $ M$ , such that $ L(M)=L(E)$ . </blockquote>

This theorem is particularly important, because it also provides an algorithm for constructing NFAs from regular expressions.

Proof:

Let $ E$ be a regular expression. We construct an NFA, with:

• exactly one initial state.
• exactly one final state.
• no transitions from the final state.

The proof is by induction over the expression structure.

Basis case $ E=\emptyset$

We construct the following automaton:

It is clear that this automaton accepts no word, and obeys the three aforementioned conditions.

Basis case $ E=\epsilon$

We construct the following automaton:

hich only accepts the empty word.

Basis case $ E=c$ where $ c$ is a symbol of the alphabet.

We construct the following automaton:

Since regular expressions have three inductive rules for constructing regular expressions (union, concatenation and Kleene-star), we have to treat three induction steps:

Induction step $ E=E_1E_2$ (concatenation)

Suppose $ E_1$ and $ E_2$ are regular expressions for which NFAs can be built (induction hypothesis). We build the following NFA which accepts all words generated by the regular expression $ E_1E_2$ .

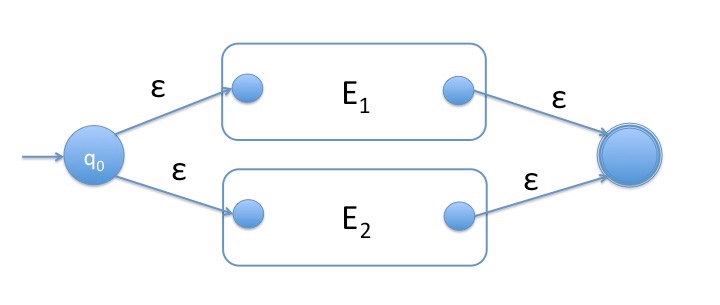
Induction step $ E=E_1\cup E_2$ (union)

Suppose $ E_1$ and $ E_2$ are regular expressions for which NFAs can be built (induction hypothesis). We build the following NFA which accepts all words generated by the regular expression $ E_1\cup E_2$ .

Induction step $ E^*$ (union)

Suppose $ E$ is regular expression for which an NFA can be built (induction hypothesis). We build the following NFA which accepts all words generated by the regular expression $ E*$ .

We illustrate the algorithmic procedure on our regular expression $ (A\cup B)(a\cup b)*(0 \cup 1)*$ . The result is shown below:

From the proof, a naive algorithm can be easily implemented. We illustrate it in Haskell:

data RegExp = EmptyString | 
              Atom Char | 
              RegExp :| RegExp | 
              RegExp :. RegExp | 
              Kleene RegExp deriving Show
 
data NFA = NFA {delta :: [(Int,Char,Int)], fin :: [Int]} deriving Show

We begin with a list-based representation of the transition function $ \delta$ . We assume the symbol e is reserved for the empty string;

-- the strategy is to increment by i, each state
relabel :: Int -> NFA -> NFA
relabel i (NFA delta fin) = NFA (map (\(s,c,s')->(s+i,c,s'+i)) delta) (map (+i) fin)

Since we have chosen to represent states as integers, we use a re-labelling function to ensure uniqueness. Re-labelling relies on state increment. For instance, by calling relabel (f1+1) n, we ensure that the NFA n will have the initial state equal to f1+1. Note that f1 is a final state in our code, which guarantees uniqueness.

toNFA EmptyString = NFA [(0,'e',1)] [1]
toNFA (Atom c) = NFA [(0,c,1)] [1]
toNFA (e :. e') = let NFA delta1 [f1] = toNFA e
                      NFA delta2 [f2] = relabel (f1+1) (toNFA e')
                  in NFA (delta1++delta2++[(f1,'e',f1+1)]) [f2]
toNFA (e :| e') = let NFA delta1 [f1] = relabel 1 (toNFA e)
                      NFA delta2 [f2] = relabel (f1+1) (toNFA e')
                  in NFA (delta1 ++ delta2 ++[(0,'e',1),
                                              (0,'e',f1+1),
                                              (f1,'e',f2+1),
                                              (f2,'e',f2+1)]) [f2+1]
toNFA (Kleene e) = let NFA delta [f] = toNFA e in NFA (delta++[(0,'e',f),(f,'e',0)]) [f]

Apart from relabelling, the code follows exactly the steps from the proof.