Maximum flow problem
Importanţă – aplicaţii practice
Algoritmii pentru determinarea unui flux maxim în rețele de trasnsport au multiple aplicații practice. Câteva exemple de aplicații sunt:
- Modelarea unei rețele de transport (canalizare, curent, petrol etc).
- Planificarea zborurilor pentru avioane.
- Segmentarea imaginilor.
- Calcul clasamente (de exemplu, la baseball).
Maximum flow problem
Puteți consulta capitolul Maximum Flow [0] pentru mai multe definiții formale. Această secțiune sumarizează principalele notații folosite în laboratoarele de PA.
Cele mai uzuale notații din laboratoarele de grafuri sunt descrise în Precizări laboratoare 07-12 (ex. $n$, $m$, $adj$, $adj\_trans$, $(x, y)$, etc).
Vom adăuga alte notații în continuarea celor introduse anterior.
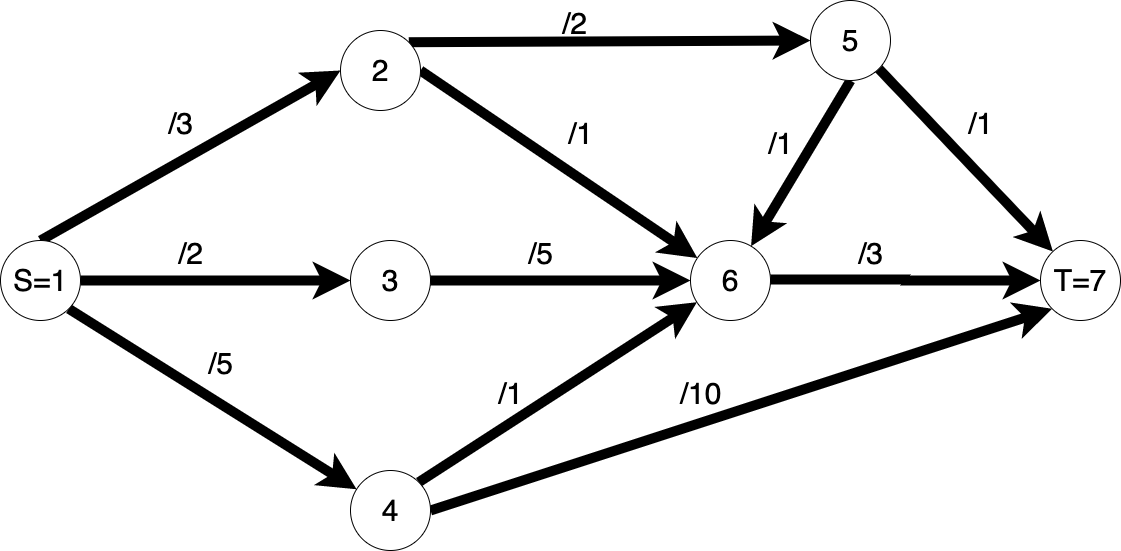
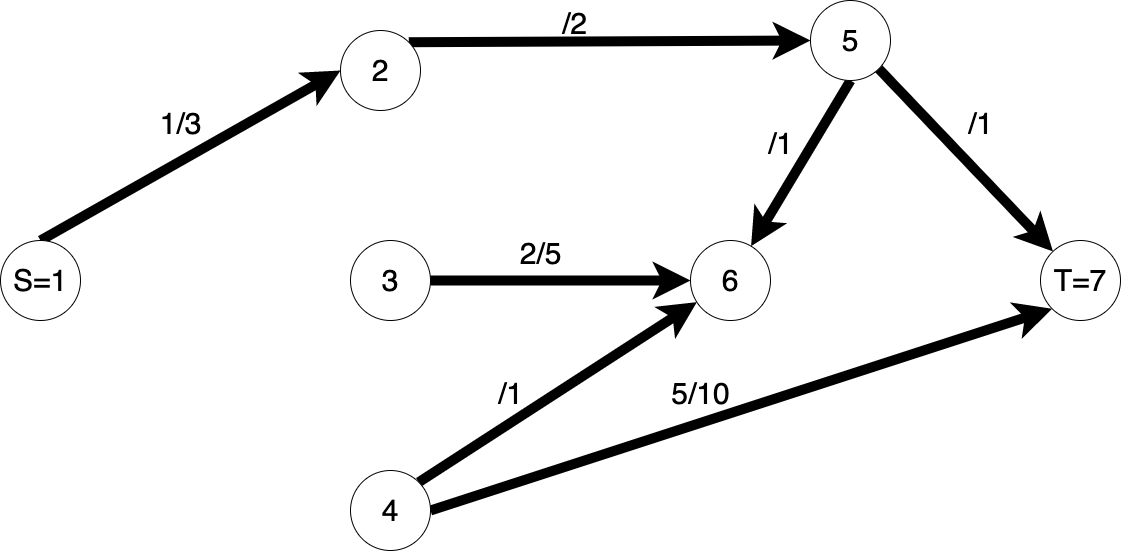
Rețea de transport / flow network: Este un graf orientat $G = (V, E)$ care respectă următoarele 3 proprietăți: 1) există două noduri speciale S (numit sursă / source) și T (numit terminal / destinație / sink); 2) există o funcție de capacitate $c: V x V -> R_{+}$ astfel încât $c(u, v) >= 0$ dacă arcul $(u, v)$ există, altfel $c(u, v) = 0$; 3) pentru orice nod $v \in V \setminus \{S, T\}$ există cel puțin o cale $S -> ... -> v -> ... T$.
Într-o rețea avem 2 noduri speciale. Vom vedea că S joacă rol de producător, iar T de consumator.
În plus, pentru simplitate, vom dori ca în graf să nu avem self-loops.
Tot pentru simplitate, în continuare vom discuta despre rețele în care capacitățile sunt numere naturale.
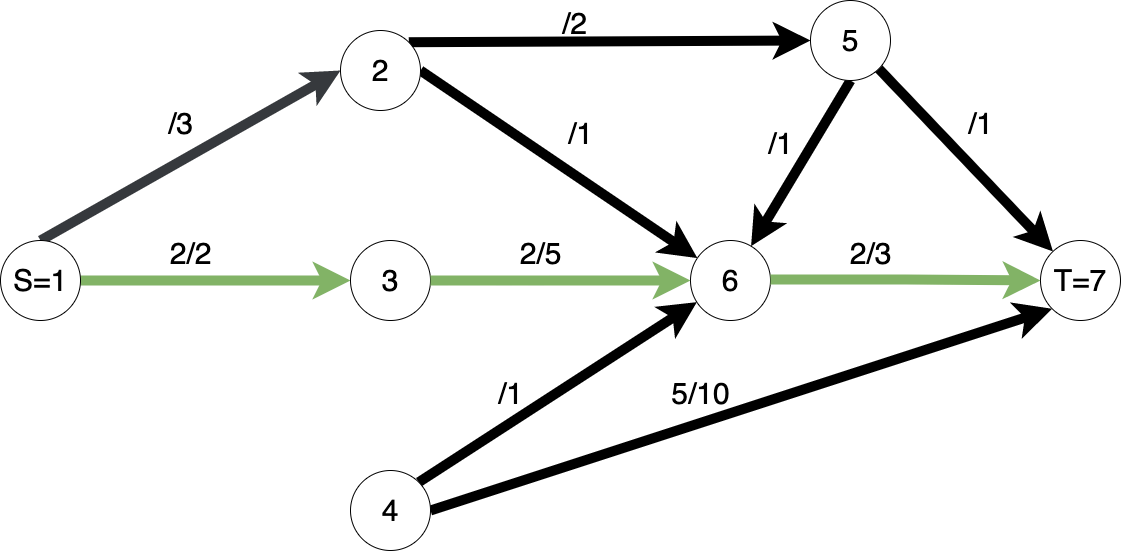
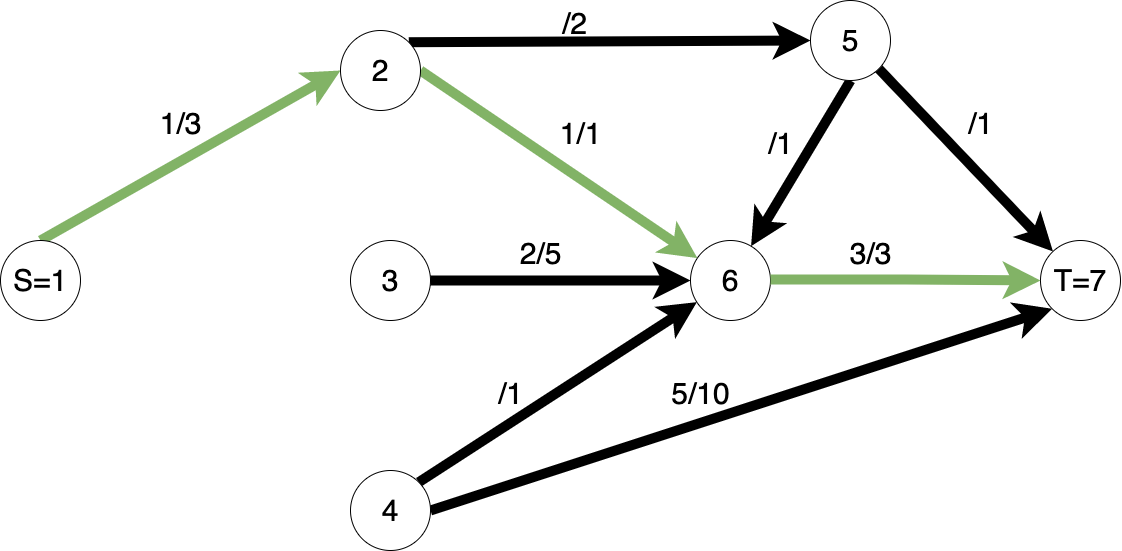
Flux / flow: O funcție $f: V x V -> R$ se numește funcție de flux într-o rețea de transport $G = (V, E)$ dacă respectă următoarele 3 proprietăți: 1) restricție de capacitate - $f(u, v) \leq c(u, v), \forall u,v \in V$; 2) antisimetrie - $f(u, v) = - f(v, u), \forall u,v \in V$; 3) conservare - $\sum f(u, v) = 0, \forall u \in V \ {S, T}, \forall v \in V$.
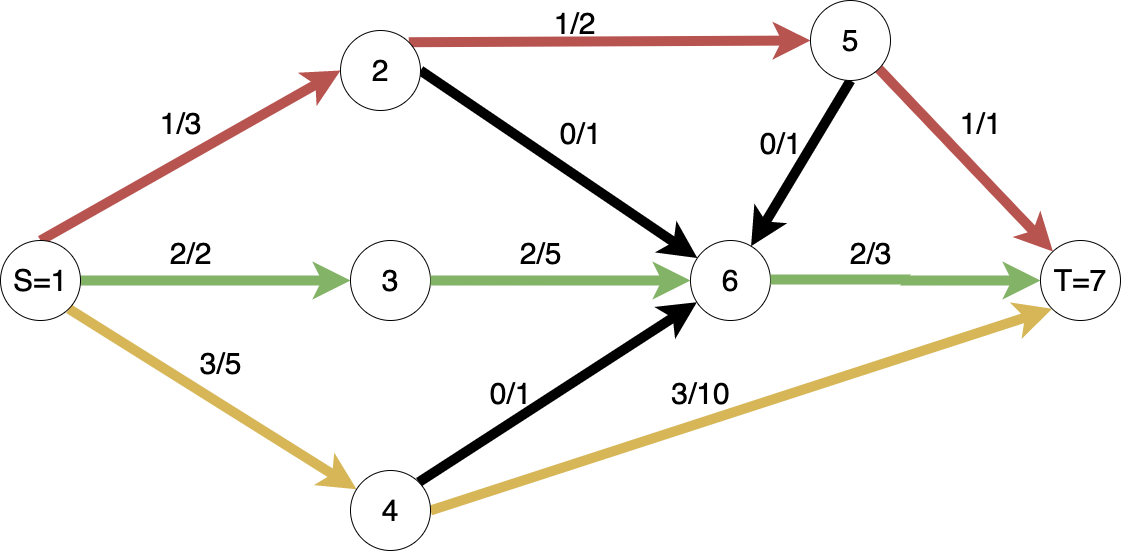
Operațiunea prin care vom aplica o anumită funcție de flux pe o rețea de transport se numește pompare: pompăm flux prin rețea / pe arcele acesteia, dinspre sursa S spre terminalul T.
Observăm că fluxul (valorile funcției) nu este unic!
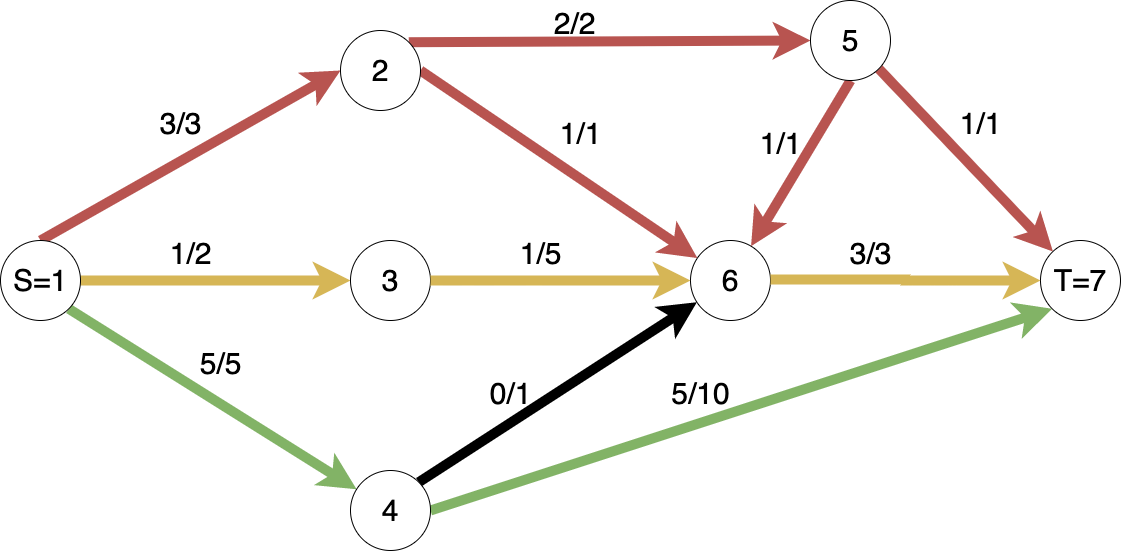
Flux maxim / maximum flow: Este o funcție de flux $f_{max}$ pentru care cantitatea de flux pompată în rețea este maximă posibil.
Capacitate reziduală / residual capacity: Diferența între capacitatea arcului și valoarea fluxului curent care este pompat prin acesta - $c_R(u, v) = c(u, v) - f(u, v)$.
Rețea reziduală / residual network: O rețea reziduală pentru $G = (V, E)$ după ce s-a pompat fluxul $f$, este rețeaua $G_R = (V, E_R)$, în care păstrăm doar muchiile pe care încă se mai poate crește cantitatea de flux - $E_R = \{(u, v) \in E | c_R(u)(v) > 0\}$.
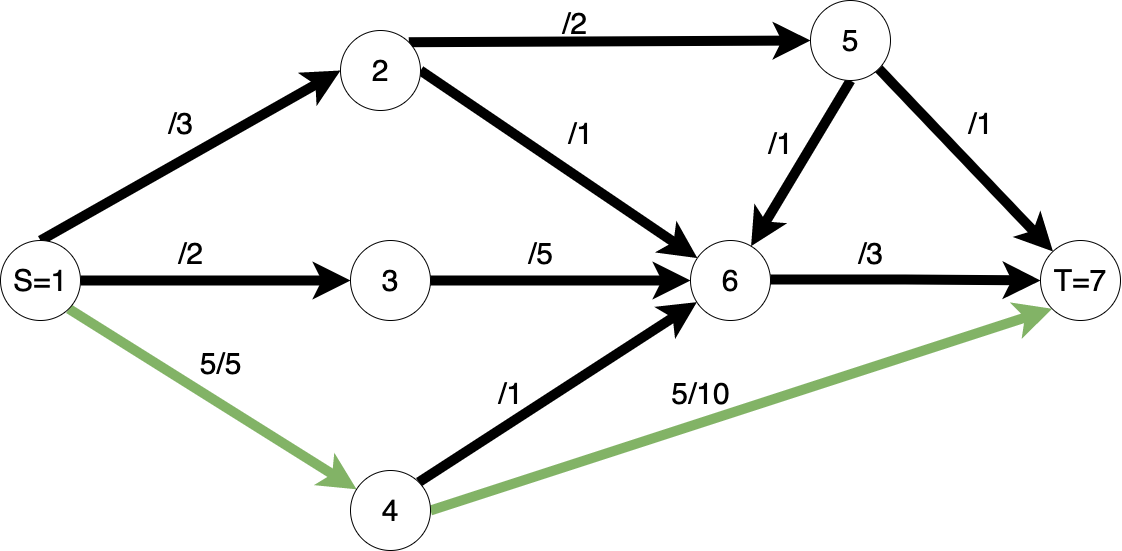
Drum de ameliorare / augmenting path: Este un drum $S -> ... -> T$ în rețeaua reziduală $G_R$ (practic este un drum pe care încă se mai poate pompa flux în plus).
Capacitate reziduală a unui drum de ameliorare / residual capacity of augmenting path: Este capacitatea minimă reziduală a unui arc de pe drum p - $c_R(p) = min(\{c_R(u, v) | (u, v) \ \in \ p\})$.
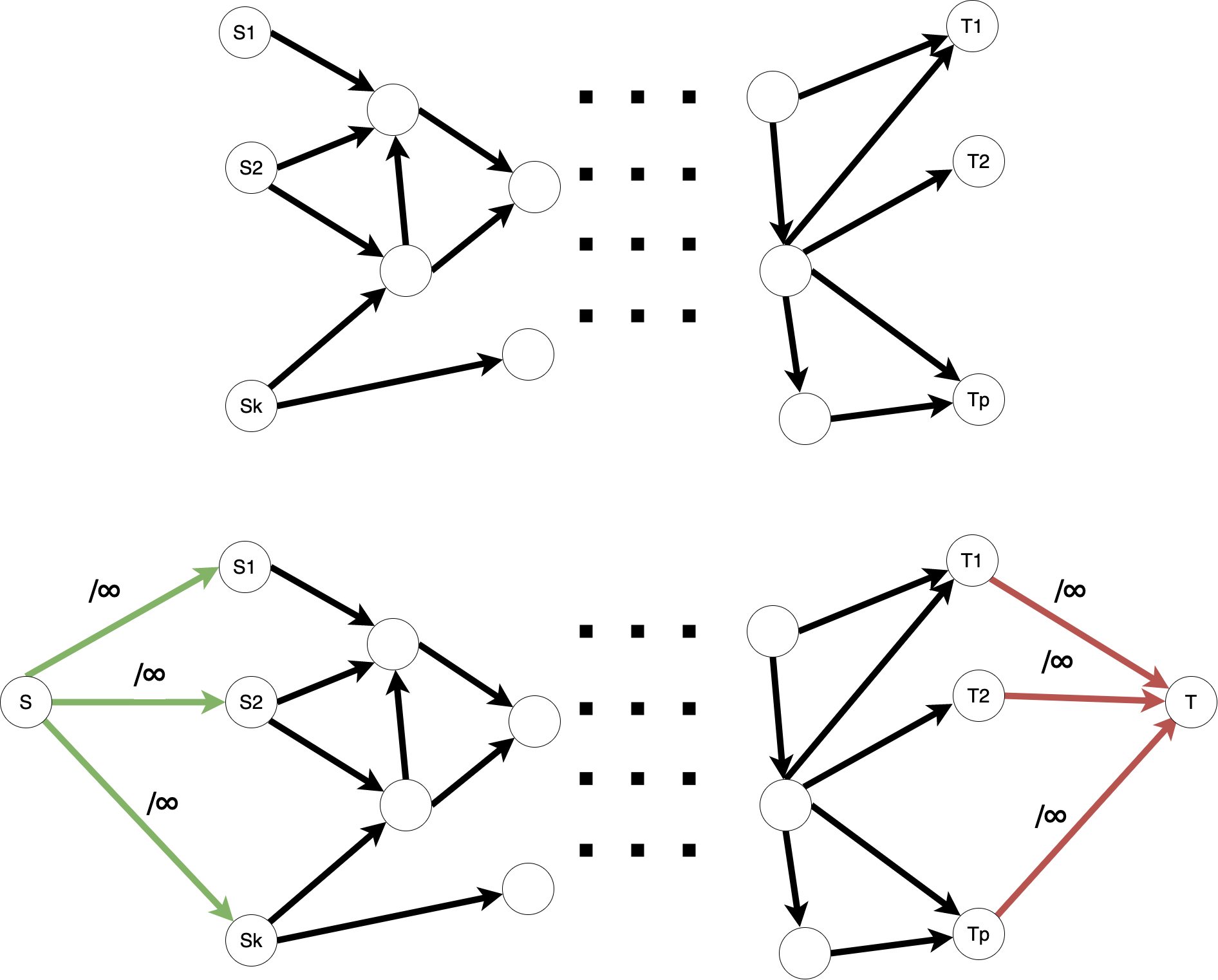
[Studiu de caz] k surse / p destinații
Maximum flow problem se poate existe considerând k surse și p destinații în aceeași rețea G. Scopul este ca să se transporte o cantitate maximă de flux total de la sursele $S_1, S_2, ... S_k$ la terminalele $T_1, T_2, ..., T_p$.
Soluția este asemănătoare ca în cazul shortest paths-problem multiple sources/destinations, adică se adaugă o sursă și o destinație fictive, care se vor lega de graful curent prin arce speciale .
Maximum flow: variants
Există o variantă puțin modificată a problemei curente - dacă pe muchii avem pe lângă capacitate și un cost asociat?
În acest caz, ne interesează să găsim un flux maxim de cost minim (maximum flow minimum cost). Problema se rezolvă în mod similar - de exemplu, algoritmul Edmonds-Karp rămăne aproximativ același, dar în locul algoritmului BFS, folosește Dijkstra pentru a determina drumurile de ameliorare.
Referințe
[0] Chapters Maximum Flow, “Introduction to Algorithms”, Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest and Clifford Stein.