• Înțelegerea noțiunilor de bază legate de programarea dinamică
• Însușirea abilităților de implementare a algoritmilor bazați pe programarea dinamică
• Înțelegerea aplicabilității practice a programării dinamice în:
  • Genetică (sequence alignment)
  • Teoria grafurilor (algoritmul Floyd-Warshall)
  • Limbaje formale și automate (algoritmul Cocke-Younger-Kasami,care analizează dacă și în ce fel un șir poate fi generat de o gramatică independentă de context)
  • Implementarea bazelor de date (algoritmul Selinger pentru optimizarea interogării relaționale)

Programarea dinamică presupune rezolvarea unei probleme prin descompunea ei în subprobleme și rezolvarea acestora. Spre deosebire de divide et impera, subprogramele nu sunt disjuncte, ci se suprapun.

Pentru a evita recalcularea porțiunilor care se suprapun, rezolvarea se face pornind de la cele mai mici subprograme și folosindu-ne de rezultatul acestora calculăm subproblema imediat mai mare. Cele mai mici subprobleme sunt numite subprobleme unitare, acestea putând fi rezolvate într-o complexitate constantă, ex:cea mai mare secvență dintr-o mulțime de un singur element.

Soluția se construiește prin programare dinamică, D[i][j]=cel mai bun cost obținut pentru primele i obiecte, având greutatea maxim j.
Relația de recurență este următoarea: D[i][j]=maxim(D[i-1][j],D[i-1][j-G[i]]+C[i]),unde G[i]=greutatea obiectului i, iar C[i]=costul obiectului.
Ideea este următoarea: La soluția curentă ori nu adăugăm deloc obiectul i, și rămânem la costul pentru i-1 obiecte, ori adăugăm obiectul i, caz în care adăugăm costul lui la costul obținut pentru primele i-1 obiecte și greutate j-G[i].

Exemplu: pentru șirul 24,12,15,8,19 răspunsul este șirul 12,15,19.
Începem prin a stabili pentru fiecare element lungimea celui mai lung subșir strict crescător care începe cu primul element și se termină în elementul respectiv. Numim această valoare best și aplicăm formula recursivă best i=1 + max(best j),cu j < i și elem j < elem i.
Aplicând acest algoritm obținem: elem 24,12,15,15,8,19 best 1,1,2,2,1,3

Pentru 24 sau 12 nu există nici un alt element în stânga lor strict mai mici decât ele, de aceea au best egal cu 1.
Pentru elementele 15 se poate găsi în stânga lor 12 strict mai mic decât ele. Pentru 19 se găsește elementul 15 strict mai mic decât el. Cum 15 deja este capăt pentru un subșir soluție de 2 elemente, putem spune că 19 este capătul pentru un subșir soluție de 3 elemente.

Pentru a găsi care sunt elementele ce alcătuiesc subșirul strict crescător putem să reținem și o 'cale de întoarcere'.
Reconstrucția astfel obținută are complexitatea O(N).
Exemplu: Subproblema care se termină în elementul 19 are subșirul de lungime maximă 3 și a fost calculată folosind subproblema care se termină cu elementul 15 (oricare din ele). Subșirul de lungime maximă care se termină în 15 a fost calculat folosindu-ne de elementul 12. 12 marchează sfârșitul reconstrucției,fiind cel mai mic element din subșir.

Fie C_n,k notat şi C(n, k) = combinări de n luate câte k.
Atunci C(n, k) = n! / ( k! (n-k)! ).

Totodată, dacă definim polinoamele P(n) := (X + 1)ⁿ , atunci se pot rescrie P(n) = ∏ (C_n,k X^k), unde k = 0,1,2,…,n.

Fie coef(P, k) = coeficientul lui X^k din polinomul P. Atunci putem scrie următoarele 2 proprietăţi:

• P1. Adunarea polinoamelor se face prin adunarea coeficienţilor de pe aceleaşi poziţii:

coef(P1 + P2, k) = coef(P1, k) + coef(P2, k), pentru orice polinoame (P1, P2) şi pentru orice număr natural k.

• P2. Înmulţirea cu un X mută coeficienţii lui X^k la X^k+1:

coef(P, k) = coef(X P, k+1), pentru orice polinom P şi pentru orice număr natural k.

Putem deduce o legătură între coeficienţii polinoamelor de tipul P(n) dacă scriem P(n + 1) = (X + 1) P(n) = X P(n) + P(n).

1. Construiți o funcție care calculează f(n), unde f = șirul lui Fibonacci;
2. Construiți o funcție care calculează f(n, k), unde f = combinări de n luate câte k;
3. implementați problema rucsacului;
4. Construiți o funcție care indică ordinea operațiilor la înmulțirea a N matrici pentru a minimiza numărul de înmulțiri între 2 numere;
5. construiți o funcție care calculează f(n) = 5ⁿ % k, unde k este o valoare fixată de la începutul programului;
6. Se dă un vector cu N elemente (v = [v1 v2 … vn]) ce poate fi secționat în piese după următoarele reguli:
   1. inițial, tot vectorul reprezintă o piesă;
   2. o piesă poate reprezenta doar o bucată continuă (nu sare peste vreun element) din vectorul inițial;
   3. secționarea unei piese duce la înlocuirea piesei respective cu 2 piese mai mici, fără a se pierde niciun element din vector;
   4. valoarea unei piese este val = (lungimea piesei) x (suma elementelor din piesă). Găsiți secțiunile ce maximizează suma valorilor pieselor.

Această metodă se poate aplica problemelor care permit descompunerea lor în subprograme independente (numele procedurii traducându-se prin împarte și stăpânește.) Așadar obținem 3 faze principale:

• Divide - împarte problema în una/mai multe probleme similare de dimensiuni mai mici.
• Stăpânește - rezolvă subproblemele recursiv (dacă dimensiunea subproblemelor este mică,se rezolvă iterativ).
• Combină - combină soluțiile sub-problemelor pentru a obține soluția problemei inițiale.

void divide_et_impera(int P[],int n,int S[]{
     if(n <= n0 )
          Determină S prin metode elementare;
     else {
          Împarte P in:P1,P2,...,Pa
          divide_et_impera(P1,S1);
          ................................................
          divide_et_impera(Pa,Sa);
          Asamblează (S1,...,Sa,S);\
     }
}

O(n) = D(n) + S(n) + C(n)
Unde D(n),S(n) și C(n) reprezintă complexitățile celor 3 pași.

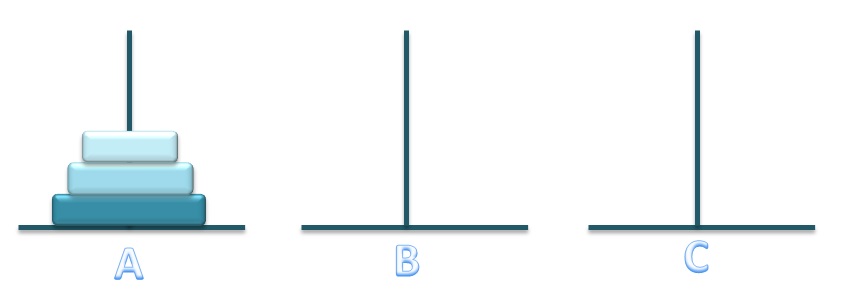
Se consideră 3 tije A,B,C si n discuri de dimensiuni distincte (1,2,….n ordinea crestătoare a dimensiunilor) situate inițial toate pe tija A în ordinea 1,2..n (de la vârf către baza).
Singura operație case se poate efectua este de selecta un disc ce se află în vârful unei tije si plasarea lui în vârful altei tije,astfel încât să nu fie așezat deasupra unui disc de dimensiune mai mică decât a sa.
Să se găsească un algoritm prin ca\re se mută toate discurile pe tija B.

Se dă un vector sortat crescător ce conține valori reale distincte și o valoare x.
Să se găsească pe ce poziție apare x (introdus de la tastatură) în vectorul dat.

int binary_search(int v[],int start,int end,int x){
     if(start > end) return;
     mid = (start+end)/2;
     if( v[mid]==x )return mid;
     if( v[mid]>x )return binary_search(v,start,mid-1,x);
     if( v[mid]<x )return binary_search(v,mid+1,end,x);
}

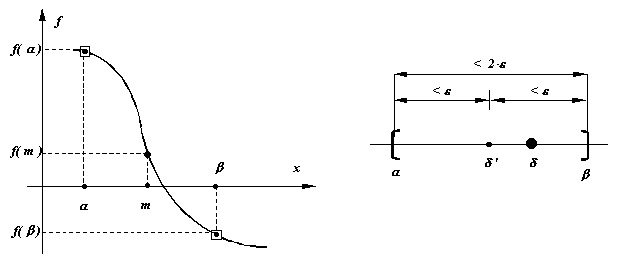
Se dă o funcție care are semne contrare în cele doua capete ale intervalului [a,b],f(α) * f(β) < 0.
Determinați o rădăcină a lui f din intervalul [a,b] cu o eroare ε.
Pentru rezolvarea problemei folosim următoarea strategie:împărțirea repetată a intervalului inițial [α,β] în jumătăți ale acestuia și selectarea intervalului jumătății în care se află soluția (Metoda bisecției)

• Fie funcția f:[α,β] → R,continuă.Determinarea aproximației Δ',a rădăcinii exacte Δ, cu eroarea ε.
• Notăm cu m mijlocul intervalului ( m=(α+β)/2 )
• Verificăm dacă f(m) * f(b) < 0,ceea ce înseamnă că soluția se află în a doua jumătate a intervalului și îi atribuim lui α valoarea lui m.
• Altfel daca f(m) * f(b) > 0,soluția se află în prima jumătate a intervalului și ii atribuim lui β valoarea lui m.
• Acest procedeu se aplică în mod repetat până când lungimea intervalului scade cu 2*ε(β - α < 2*ε)
  

Fractalii de tip Divide-et-Impera sunt construiți, după cum sugerează numele, prin spargerea componentei principale în mai multe părți și aplicarea spargerii asupra componentelor mai mici rezultate, până când se ajunge la cazul (componenta) de bază. La aceasta se ajunge efectuând un număr de apeluri ale funcției recursive egal cu numărul introdus.
Fractalii generați prin metode Divide-et-Impera au la bază un model simplu, pe baza căruia se adaugă (în cazul arborilor și al triunghiului lui Sierpinski) sau se înlocuiesc (în cazul fractalilor Koch) segmente, după o regulă bine definită, așa cum se poate observa:

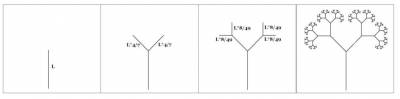
Se calculează coordonatele punctului de sfârșit al liniei ce trebuie reprezentată, în funcție de lungimea acesteia și de unghiul sub care va fi desenată.
Apoi este apelată de doua ori funcția de desenare, cu parametrii modificați: punctele de început ale următoarei linii vor avea coordonatele punctului de sfârșit al ultimelei linii desenate, lungimea va fi micșorată printr-un raport stabilit (ex: 4/7), numărul nivelului va fi cu o unitate mai mic, iar unghiul va fi modificat cu 45° (o dată în plus,a doua oară în minus)
Condiția de efectuare a instrucțiunilor din funcție este ca numărul de niveluri ale fractalului să fie mai mare decât 0.

În cazul fractalilor de tip Koch, liniile nu se adaugă, ci se înlocuiesc. Pentru calcularea lungimii, poziției și unghiului fiecărui segment al liniei, funcția este apelată de n ori,segmentul fiind desenat atunci când nivelul devine 0.
La fractalul de tip Koch triunghiular, coordonatele care ne interesează se află la prima treime, a doua treime și jumatatea segmentului. La fiecare dintre acestea, unghiul de desenare se modifică cu 60°,-120°, respectiv 60°.

Ca și în cazul arborelui,fractalul Sierpinski este construit prin adăugarea de linii la imaginea generată până în acel moment, până când nivelul devine mai mic decât n.
Se pornește de la un triunghi în care au fost desenate liniile mijlocii și se desenează liniile mijlocii ale triunghiurilor mai mici marginale formate.

Aplicații practice!

• Teoria fractalilor a crescut interesul în domeniul compresiei de date și imagine, cu scopul reducerii cantității de date necesare pentru reprezentarea unei imegini.
  
• Compresia este folosită în special pentru stocarea sau transmiterea imaginilor.
  
• Compresia cu fractali se bazează pe faptul că în anumite imagini, părți ale imaginii seamănă cu părți ale aceeași imagini.
  
• Tehnica copiază imaginea originală în 2 seturi: ranguri și domenii, apoi computer-ul face legătura fiecărui rang cu un domeniu și produce o trasformare de la domeniu la rang:
  

Ca să putem introduce noțiunea de parser top-down este necesar să definim etapele compilării unui program C:

• Analiza lexicală - Descompune programul sursă în identificatori, cuvinte rezervate, constante ,operatori și îi introduce în tabela de simboluri sub formă codificată.
• Analiza sintactică - Se caută structuri sintactice, cum ar fi expresii, liste, proceduri, plasându-le într-un arbore de derivare
• Analiza semantica - Generează un grup de instrucțiuni simple cu format fix (cod intern)
• Optimizarea codului
• Generarea codului - Alocă zone de memorie pentru păstrarea datelor în timpul execuției și produce codul obiect (în limbaj de asamblare)
• Gestiunea structurilor de date
• Tratarea erorilor
  

Vom trata problema analizei sintactice care are două obiective principale:

• Stabilește dacă un cuvânt dat aparține sau nu limbajului
• Determină arborele de derivare corespunzător cuvântului conform principiului Divide et Impera, problema fiind descompusă în alte doua subprobleme de același tip

1. Simulați un proces de back-up a unor date fără a partiționa mediul de stocare.

2. Folosiţi un algoritm de tip Greedy pentru a găsi numărul minim de bancnote necesare pentru a da o anumită sumă de bani ca rest. Presupunem numai valori întregi pentru suma de bani şi următoarele bancnote: {1, 5, 10, 50, 100} (RON).

3*. Găsiţi un exemplu pentru care un algoritm de tip Greedy nu ar funcţiona pentru o problemă similară, dar care foloseşte următoarele bancnote: {1, 3, 5, 15, 30, 50, 150}. Încercaţi să explicaţi de ce, în acest caz, tehnica Greedy nu mai e optimă.

4*. Găsiţi un exemplu pentru care varianta Greedy (pură) de rezolvare a problemei TSP (comis-voiajor) găseşte o soluţie, dar aceasta nu este optimă.

5. Aproximaţi, printr-o abordare de tip Divide et Impera, cu o eroare (relativă) de maxim 1e-6, funcţia sqrt(n) (extragerea rădăcinii pătrate a unui număr). Nu aveţi voie să folosiţi nicio funcţie din “math.h”. Încercaţi să extindeţi exerciţiul pentru extragerea radicalului de ordin 3.

6. Aproximaţi, printr-o abordare de tip Divide et Impera, cu o eroare (relativă) de maxim 1e-3, funcţia lg(n) (extragerea logaritmului în baza 10). Aveţi voie să vă folosiţi de funcţia pow(bază, exp) din “math.h”.

7*. Problema 5 (extras logaritm) fără a vă folosi de funcţia pow, ci doar de funcţia construită la 4 (extragerea radicalului).

8**. Se dă un vector cu N numere întregi, apoi se fac un număr de C cereri de tipul “Calculează suma numerelor de la poziţia i până la poziţia j”. Reduceţi sub O(N * C) timpul necesar pentru a răspunde la toate cererile dacă N este prea mare pentru a reţine în memorie toate perechile de sume(de la orice i la orice j) şi, în acelaşi timp, C > N. (Variantă alternativă - minim în loc de sumă)