Laborator 7 - ABC și Heap

Responsabili

• Alexandra Lache
• Traian Dobrescu

În urma parcurgerii laboratorului, studentul va fi capabil să:

• înțeleagă structura și proprietățile unui arbore binar de căutare;
• construiască, în limbajul C, un arbore binar de căutare;
• realizeze o parcurgere a structurii de date prin mai multe moduri;
• realizeze diferite operații folosind arborii binari de căutare;

• definească proprietățile structurii de heap;
• implementeze operații de inserare, ștergere și căutare care să păstreze proprietatea de heap;
• folosească heap-ul pentru a implementa o metodă de sortare eficientă.

Un arbore binar de căutare este un arbore binar care are în plus următoarele proprietăți:

• cheile stocate în noduri (informația utilă) aparțin unei mulțimi peste care există o relație de ordine totală
• cheia dintr-un nod oarecare este mai mare decât cheile tuturor nodurilor din subarborele stâng și este mai mică decât cheile tuturor nodurilor ce compun subarborele drept

Arborii binari de căutare permit menținerea datelor în ordine și o căutare rapidă a unei chei, ceea ce îi recomandă pentru implementarea de mulțimi și dicționare ordonate.

O importantă caracteristică a arborilor de căutare, este aceea că parcurgerea inordine produce o secvență ordonată crescător a cheilor din nodurile arborelui.

Valoarea maximă dintr-un arbore binar de căutare se află în nodul din extremitatea dreaptă și se determină prin coborârea pe subarborele drept, iar valoarea minimă se află în nodul din extremitatea stângă, determinarea fiind simetrică.

Căutarea unei chei într-un arbore binar de căutare este asemănătoare căutării binare: cheia căutată este comparată cu cheia din nodul curent (inițial nodul rădăcină). În funcție de rezultatul comparației apar trei cazuri:

• acestea coincid –> elementul a fost găsit
• elementul căutat este mai mic decât cheia din nodul curent –> căutarea continuă în subarborele stâng
• elementul căutat este mai mare decât cheia din nodul curent → căutarea continuă în subarborele drept

Pseudocod:

bool căutare(nod, cheie) {
  if nod == NULL
    return false;
  if nod.cheie == cheie
    return true;
 
  if cheie < nod.cheie
    return căutare(nod.stanga, cheie);
  else
    return căutare(nod.dreapta, cheie);
}

Inserarea unui nod se face în funcție de rezultatul comparației cheilor, în subarborele stâng sau drept. Dacă arborele este vid, se creează un nod care devine nodul rădăcină al arborelui. În caz contrar, cheia se inserează ca fiu stâng sau fiu drept al unui nod din arbore.

Ștergerea unui nod este o operație puțin mai complicată, întrucât presupune o rearanjare a nodurilor. Pentru eliminarea unui nod dintr-un arbore binar de căutare sunt posibile următoare cazuri:

• nodul de șters nu există → operația se consideră încheiată
• nodul de șters nu are succesori → este o frunză
• nodul de șters are un singur succesor
• nodul de șters are doi succesori

Complexitatea operațiilor (căutare, inserare, ștergere) într-un arbore binar de căutare este - pe cazul mediu - O(log n).

Mai sus am considerat arborii binari ca fiind o înlănțuire de structuri, legate între ele prin pointeri la descendenții stâng, respectiv drept. Această reprezentare are avantajul flexibilității și a posibilității de a crește sau micșora dimensiunea arborelui oricât de mult, cu un efort minim. Cu toate acestea, metoda precedentă nu poate fi folosită atunci când este nevoie de o reprezentare compactă a arborelui în memorie (de exemplu pentru stocarea într-un fișier), pentru că acei pointeri nu sunt valizi decât în cadrul programului curent.

Din acest motiv, există câteva moduri de a stoca arborii într-o structura liniară de date (vectori), dintre care:

• Înlocuirea pointer-ilor din structurile asociate nodurilor cu întregi ce reprezintă indici într-un vector de astfel de structuri. Primul element din vector va fi rădăcina arborelui, și va exista un contor curent (la nivelul întregului vector) care indică următoarea poziție liberă. Atunci când un nod trebuie adăugat în arbore, i se va asocia valoarea curentă a contorului, iar acesta va fi incrementat. În nodul părinte se va reține indicele în vector al noului nod, în locul adresei lui în memorie (practic acesta este un mic mecanism de alocare de memorie, pe care îl gestionăm noi).
• Eliminarea totală a informației legate de predecesori, și folosirea unei formule de calcul a părintelui și a descendenților unui nod pe baza indicelui acestuia în vector.

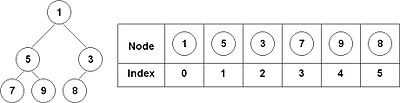
Pentru un arbore binar, cea de-a doua modalitate se implementează conform figurii de mai jos:

Reprezentarea liniara (sub formă de vector) pentru un arbore binar complet devine:

Se constată că poziția nodului rădăcină în vector este 0, iar pentru fiecare nod în parte, părintele și descendenții se pot calcula după formulele:

• Părinte(i) = (i - 1) / 2, unde i este indicele nodului curent
• IndexStânga(i) = 2 * i + 1, unde i este indicele nodului curent
• IndexDreapta(i) = 2 * i + 2, unde i este indicele nodului curent

În cele ce urmează vom considera un heap ca fiind de fapt un min-heap. Noțiunile sunt perfect similare și pentru max-heap-uri.

Un min-heap binar este un arbore binar în care fiecare nod are proprietatea că valoarea sa este mai mare sau egală cu cea a părintelui său.

Într-o enunțare echivalentă:

Un min-heap binar este un arbore binar în care fiecare nod are proprietatea că valoarea sa este mai mică sau egală decât cea a tuturor descendenților săi.

h[parinte(x)] <= h[x]

h[x] reprezintă valoarea nodului x, din vectorul h asociat arborelui.

În mod similar, un max-heap are semnul inegalității inversat. Astfel, putem defini și recursiv proprietatea de heap pentru orice (sub)arbore:

• nodul rădăcină trebuie să respecte proprietatea de heap (inegalitatea);
• cei doi subarbori descendenți sa fie heap-uri.

Având implementate cele două operații de bază, putem defini operațiile uzuale de manipulare a heap-urilor:

Operația întoarce valoarea minimă din min-heap. Valoarea se va afla la indexul 0 al vectorului de implementare a heap-ului.

Adaugă o nouă valoare la heap, crescându-i astfel dimensiunea cu 1.

Algoritmul pentru această funcție este următorul:

1. introducem elementul de inserat pe prima poziție liberă din vectorul de implementare a heap-ului (în principiu dimVect);
2. “împingem” elementul adăugat în vector până la poziția în care se respectă proprietatea de heap; veți folosi funcția pushUp.

push(heap, X)
{
    heap[dimVec] = X;
    dimVec++;
    pushUp(heap, dimVec - 1);
}

Funcția aceasta scoate valoarea minimă din heap (și reactualizează heap-ul). Poate întoarce valoarea scoasă din heap.

Pentru a face operația de pop veți urma pașii:

1. elementul minim din heap (de pe prima poziție) va fi interschimbat cu elementul de pe ultima poziție a vectorului;
2. dimensiunea vectorului va fi redusă cu 1 (pentru a ignora ultimul element, acum cel pe care doream să-l înlăturăm)
3. vom “împinge” nodul care se afla acum în rădăcina heap-ului către poziția în care trebuie sa fie pentru a fi respectată proprietatea de heap; acest lucru se va face cu funcția pushDown.

extractMin(heap)
{
    interschimba(heap[0], heap[dimVec - 1]);
    dimVect--;
    pushDown(heap, 0);
}

Întrucât operațiile de extragere a minimului și de adăugare/reconstituire sunt efectuate foarte eficient (complexități de O(1), respectiv O(log n)), heap-ul poate fi folosit într-o multitudine de aplicații care necesită rapiditatea unor astfel de operații. O aplicație importantă o reprezintă sortarea, care poate fi implementată foarte eficient folosind heap-uri. Complexitatea acesteia este O(n*log n), aceeași cu cea de la quick sort și merge sort.

Se poate implementa inserând, pe rând, în heap, toate elementele din vectorul nesortat. Apoi într-un alt șir se extrag minimele. Noul șir va conține vechiul vector sortat.

HeapSort(heap) 
{
    heap = ConstruiesteMaxHeap();
    for (i = dimHeap - 1; i >= 1; i--) 
    {
        // Punem maximul la sfarsitul vectorului
        interschimba(heap[0], heap[i]);
        // 'Desprindem' maximul de heap (valoarea ramanand astfel in pozitia finala)
        dimHeap--;
        // Reconstituim heap-ul ramas
        pushDown(heap, 0);
    }
}

Deși la prima vedere nu există mari diferențe între cele două structuri de date, ele sunt complet diferite. Se poate observa că ele diferă atât la nivelul implementării (abc:pointeri către fii vs heap:vector), cât și al complexităților operațiilor specifice. Totuși, deși ambele se pot folosi în rare cazuri pentru același scop (fără a fi la fel de eficiente), ele au întrebuințări diferite.

ABC

• Se folosește pentru a implementa arbori echilibrați, precum AVL, Red-Black.
• Prezintă toate avantajele unui vector sortat, venind în plus cu inserare în timp logaritmic.
• Nu este mereu echilibrat.

HEAP

• Heap-ul stă la baza implementării cozii de priorități și a algoritmului heapsort.
• Se poate folosi pentru găsirea eficientă a celui de-al k-lea cel mai mic/mare (minheap/maxheap) element.
• Este mereu un arbore echilibrat (complet).

1) [3.5p] BST

Task1 va testa operațiile de insert, remove și afișarea (în ordine) a elementelor introduse în BST.

2) [3.5p] Heap

Task2 va abstractiza următoarea problemă:

Avem un clasament în care pot fi introduse echipe - nume + scor.

Trebuie să efectuăm N operații de tipul:

• 1 - introducem o nouă echipă în clasament
• 2 - afișăm prima echipă din clasament
• 3 - eliminăm prima echipă din clasament
• 4 - se incheie programul

La final, vom afișa topul echipelor rămase în joc.

3) [BONUS 2p] BST K-Smallest

Se dă un arbore binar de căutare cu valori de tip întreg. Să se întoarcă a k-a cea mai mică valoare din arbore.

1. Vizualizare Binary Search Tree
2. Binary Search Tree
3. Binary Heap
4. Heap Sort