Table of Contents
Haskell: Structuri de date funcționale
- Data publicării: 11.04.2023
- Data ultimei modificări: 04.05.2023
- Deadline hard: ziua laboratorului 10 (11 pentru seria CB)
Obiective
- Aplicarea mecanismelor funcționale, de tipuri (inclusiv polimorfism) și de evaluare leneșă din limbajul Haskell.
- Exploatarea evaluării leneșe pentru decuplarea conceptuală a prelucrărilor realizate.
Descriere generală și organizare
Tema urmărește familiarizarea cu specificul implementării structurilor de date în limbajele funcționale, problema eficienței fiind centrală. În limbajele imperative, eficiența este parțial alimentată de posibilitatea modificărilor distructive; de exemplu, actualizând în timp constant un element dintr-un vector. Prin contrast, în limbajele funcționale, modificările distructive sunt de obicei evitate, cu consecința persistenței structurilor de date. Cu alte cuvinte, dacă în abordarea imperativă dispunem de obicei doar de ultima variantă a unei structuri, care încorporează întregul istoric de modificări ale acesteia, în abordarea funcțională putem dispune simultan de toate versiunile intermediare ale acelei structuri. Ultima constrângere pare să impună costuri semnificative asupra implementării funcționale a structurilor de date, cu pierderi importante de eficiență. Vestea bună este că o reproiectare perspicace a acestor structuri poate recupera eficiența operațiilor; astfel, se combină complexitatatea comparabilă cu cea a structurilor imperative cu beneficiile purității funcționale.
Tema propune drept studiu de caz implementarea în Haskell a unei cozi de priorități, utilizând heap-uri binomiale. Implementarea imperativă standard a unui heap utilizează vectori și mizează pe accesul aleator în timp constant. După cum știm, listele înlănțuite din limbajele funcționale nu se pretează unei abordări fundamentate pe accesul aleator, care se realizează în timp liniar. Prin urmare, vom utiliza o reprezentare alternativă, în forma listelor de arbori binomiali, care oferă o complexitate logaritmică pentru toate operațiile, inclusiv pentru cea de combinare a două heap-uri, care în abordarea imperativă standard se realizează în timp liniar.
Tema este împărțită în 3 etape:
- una pe care o veți rezolva după laboratorul 7, cu deadline în ziua laboratorului 8 (9 pentru seria CB)
- una pe care o veți rezolva după laboratorul 8, cu deadline în ziua laboratorului 9 (10 pentru seria CB)
- una pe care o veți rezolva după laboratorul 9, cu deadline în ziua laboratorului 10 (11 pentru seria CB).
Deadline-ul depinde de semigrupa în care sunteți repartizați. Restanțierii care refac tema și nu refac laboratorul beneficiază de ultimul deadline, și anume în zilele de 02.05, 09.05, respectiv 16.05.
Rezolvările tuturor etapelor pot fi trimise până în ziua laboratorului 10 (deadline hard pentru toate etapele). Orice exercițiu trimis după un deadline soft se punctează la jumătate. Cu alte cuvinte, nota finală pe etapă se calculează conform formulei: n = (n1 + n2) / 2 (n1 = nota obținută înainte de deadline; n2 = nota obținută după deadline). Când toate submisiile preced deadline-ul, nota pe ultima submisie constituie nota finală (întrucât n1 = n2).
În fiecare etapă, veți valorifica ce ați învățat în săptămâna anterioară și veți avea la dispoziție un schelet de cod, cu toate că rezolvarea se bazează în mare măsură pe etapele anterioare. Enunțul caută să ofere o imagine de ansamblu atât la nivel conceptual, cât și în privința aspectelor care se doresc implementate, în timp ce detaliile se găsesc direct în schelet.
Etapa 1
Operațiile pe heap-uri binomiale (cum este adăugarea unui nou element) sunt foarte similare conceptual celor pe numere binare (de exemplu, incrementare). Prin urmare, această etapă are un rol pregătitor, propunând o reprezentare a numerelor binare și definirea unor operații standard cu acestea. Heap-urile binomiale vor fi introduse propriu-zis în etapa 2.
Construcțiile și mecanismele de limbaj pe care le veți exploata în rezolvare sunt:
- liste, pentru reprezentarea numerelor binare ca secvențe potențial infinite de biți
- funcționale pe liste, ocazie cu care veți intra în contact atât cu cele standard, care se găsesc și în Racket, cât și cu altele specifice în Haskell
- list comprehensions, pentru descrierea concisă a unor transformări
- evaluare leneșă, implicită în Haskell, pentru decuplarea conceptuală a transformărilor din cadrul unei secvențe.
Modulul de interes din schelet este BinaryNumber, care conține reprezentarea numerelor binare și operațiile pe care trebuie să le implementați:
- tipul
BinaryNumberdefinește reprezentarea numerelor binare - funcția
toDecimalconvertește din reprezentarea binară în cea zecimală - funcția
toBinaryrealizează conversia inversă - funcțiile
incșidecincrementează, respectiv decrementează cu 1 un număr binar, ținând cont bineînțeles de transport, respectiv împrumut - funcția
addadună două numere binare - funcția
stackpregătește terenul pentru înmulțirea a două numere binare, simulând maniera în care am dispune numerele pe hârtie, unul sub celălalt - funcția
multiplyrealizează înmulțiri propriu-zise.
Găsiți detaliile despre funcționalitate și despre constrângerile de implementare, precum și exemple, direct în schelet. Aveți de completat definițiile care încep cu *** TODO ***.
Pentru rularea testelor, încărcați în interpretor modulul TestBinaryNumber și evaluați main.
Este suficient ca arhiva pentru vmchecker să conțină modulul BinaryNumber.
Etapa 2
În această etapă, veți începe implementarea unei cozi de priorități, utilizând heap-uri binomiale, prezentate mai jos. Coada va expune operații precum adăugarea unei chei, alături de prioritatea asociată, combinarea a două cozi, determinarea cheii cu prioritate minimă, precum și eliminarea acesteia. Toate operațiile vor avea complexitate logaritmică în dimensiunea cozii. Din moment ce ne concentrăm pe prioritățile minime, vorbim implicit despre un min priority queue sau min-heap.
Construcțiile și mecanismele noi de limbaj pe care le veți exploata în rezolvare, pe lângă cele din etapa 1, sunt:
- tipurile de date utilizator.
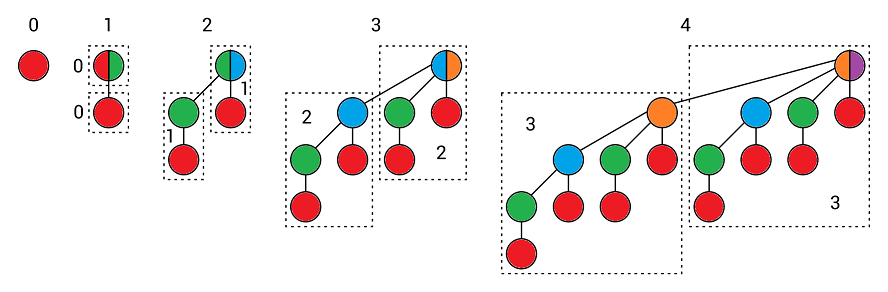
Înainte de prezentarea heap-urilor binomiale, introducem mai întâi conceptul de arbore binomial, care stă la baza primelor. Aceștia se construiesc recursiv, ca în fig. 1 de mai jos:
- cel mai simplu arbore binomial nevid este cel cu un singur nod
- atașându-i unui arbore existent o copie a sa (din perspectivă structurală, nu neapărat a conținutului) ca cel mai din stânga copil, se obține tot un arbore binomial.
Fig. 1. Arbori binomiali. Adaptare după oreilly.com.
Introducem de asemenea următoarele atribute ale unui arbore binomial:
- rangul reprezintă numărul de copii ai rădăcinii
- dimensiunea este numărul total de noduri, egal cu 2 ridicat la puterea rangului.
Astfel, în fig. 1:
- primul arbore are rangul 0 și dimensiunea 1
- atașând la un arbore de rang
r-1și dimensiune2^(r-1)o copie de-a sa, obținem un arbore de rangrși dimensiune2^r; nodurile bicolore surprind creșterea rangului unui nod de lar-1larîn urma atașării copiei.
În fig. 1, se observă mai mulți arbori binomiali, cu ranguri între 0 și 4, și că înălțimea unui arbore este egală cu rangul său. De asemenea, transpare o proprietate care derivă din modalitatea de construcție: copiii unui nod de rang r au rangurile r-1, r-2, …, 1, 0, exact în această ordine descrescătoare. De exemplu, copiii rădăcinii de rang 4 au rangurile 3, 2, 1, 0. Numele de arbore binomial vine de la faptul că, pe nivelul i din arborele de rang r, numărul de noduri este dat de coeficientul binomial „combinări de r luate câte i”.
Continuăm cu prezentarea heap-urilor binomiale. Acestea nu sunt decât liste de arbori binomiali, cu constrângerea suplimentară că arborii trebuie să respecte și proprietatea de heap, i.e. rădăcina are prioritate mai mică decât copiii și analog pentru subarbori. Având în vedere faptul că toți arborii binomiali au dimensiuni puteri ale lui 2, principala întrebare este cum distribuim elementele heap-ului în cadrul acestor arbori, presupunând că numărul total de elemente nu este putere a lui 2. Aici intervine reprezentarea binară a numerelor din etapa 1. Dacă dimensiunea heap-ului este n, având reprezentarea binară [b_0, b_1, ..., b_m], unde m = [lg n] (parte întreagă), atunci, pentru fiecare bit 0, vom avea un arbore vid, și pentru fiecare bit b_r egal cu 1 vom avea un arbore de rang r, și implicit dimensiune 2^r.
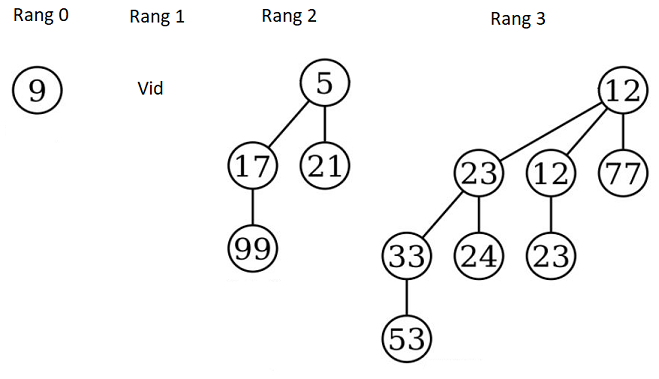
Exemplificăm ideea de mai sus cu un heap cu 13 elemente, reprezentarea binară a dimensiunii fiind [1, 0, 1, 1]. Aceasta înseamnă că avem un arbore de rang 0 (dimensiune 1), niciun arbore de rang 1, un arbore de rang 2 (dimensiune 4) și un arbore de rang 3 (dimensiune 8), ca în fig. 2. Observați de asemenea respectarea proprietății de heap de către fiecare dintre cei trei arbori.
Fig. 2. Heap binomial. Adaptare după bartleby.com.
Vom vedea în continuare cum unele operațiile asupra heap-urilor binomiale le oglindesc pe cele asupra numerelor binare. De exemplu, operația de inserare a unui element corespunde incrementării unui număr binar. La fel cum, în cazul numerelor binare, operația de incrementare presupune poziționarea unui bit 1 în dreptul primului bit al reprezentării numărului de incrementat și modificarea succesivă a biților curent și următori, în caz de transport, operația de inserare a unui element într-un heap binomial presupune poziționarea unui arbore de rang 0 (dimensiune 1) în dreptul primului arbore existent în heap și modificarea succesivă a arborelui curent și eventual a următorilor. Dacă este destul de clar ce înseamnă a aduna doi biți, rămâne de clarificat ce înseamnă a „aduna” doi arbori binomiali:
- adunarea oricărui arbore cu un arbore vid produce primul arbore
- adunarea a doi arbori nevizi cu același rang conduce la atașarea unui arbore ca cel mai din stânga copil al celuilalt, adică tocmai principiul recursiv de construcție a arborilor binomiali; arborele rezultant, cu rang mai mare cu 1 decât al arborilor constituenți, devine transport.
De remarcat că niciodată nu vom fi puși în situația de a aduna doi arbori nevizi cu ranguri diferite. Rămâne de ales arborele care joacă rolul de copil al celuilalt; din moment ce trebuie conservată proprietatea de heap, copil va deveni arborele cu prioritatea mai mare.
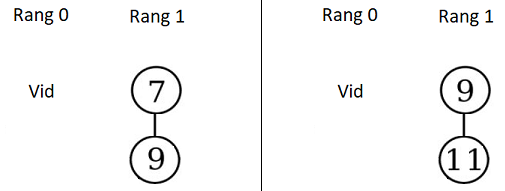
Exemplificăm inserarea unui nou element în heap-ul din fig. 2. Ne vom concentra pe pozițiile de rang 0 și 1, întrucât cele de rang 2 și 3 nu vor fi afectate. Rezultatul se observă în fig. 3:
- dacă prioritatea noului element este mai mică (7), arborele existent (9) devine copilul acestuia (fig. 3, stânga)
- dacă prioritatea noului element este mai mare (11), noul arbore devine copil al celui existent (9) (fig. 3, dreapta).
În ambele cazuri, rezultă un transport în forma unui arbore de rang 1, care îl înlocuiește pe cel vid din heap-ul original; de asemenea, dispare arborele de rang 0. Dacă în heap-ul original ar fi existat deja un arbore de rang 1, procesul de atașare și propagare a transportului ar fi continuat recursiv, către poziția de rang 2 ș.a.m.d.
Fig. 3. Inserarea în heap-ul binomial din fig. 2.
Cum reprezentarea binară a dimensiunii heap-ului conține un număr logaritmic de biți, deci un număr logaritmic de arbori (vizi sau nevizi), iar atașarea unui arbore la altul se face în timp constant, inserarea are complexitate logaritmică.
Având în vedere că toți arborii respectă proprietatea de heap, i.e. rădăcina este elementul cu prioritate minimă din fiecare arbore, operația de determinare a elementului cu prioritate minimă din întregul heap presupune identificarea rădăcinii cu prioritate minimă. În exemplul din fig. 2, prioritatea minimă este 5, aferentă rădăcinii arborelui de rang 2. Dacă există mai multe rădăcini cu prioritate minimă, se alege cea care apare prima în lista de arbori. Urmând un raționament similar celui din paragraful anterior, rezultă că și această operație are complexitate logaritmică.
Ultima operație implementată în această etapă este cea de combinare (engl. merge) a două heap-uri. Aceasta o oglindește pe cea de adunare a două numere binare din etapa 1. La fel cum, în cazul numerelor binare, se adună mai întâi biții de pe poziția 0, apoi 1 etc., în cazul heap-urilor binomiale, se începe cu adunarea arborilor de pe poziția de rang 0, apoi rang 1 ș.a.m.d., ținând cont bineînțeles de eventualul transport. Din motive similare celor de mai sus, și această operație are complexitate logaritmică.
Modulul de interes din schelet este BinomialHeap, care conține reprezentarea arborilor binomiali și a heap-urilor binomiale, precum și operațiile descrise mai sus:
- tipul
BinomialTree p k, deja definit, desemnează arbori binomiali având noduri cu priorități de tippși chei de tipk; în mod evident, prioritățile trebuie să fie ordonabile - tipul
BinomialHeap p k, deja definit, denotă heap-uri binomiale având elemente cu priorități de tippși chei de tipk - funcția
attachpermite atașarea unui arbore ca cel mai din stânga copil al altuia, în vederea conservării proprietății de heap - heap-ul vid,
emptyHeap - funcțiile
insertTreeșiinsertpermit inserarea unui nou element într-un heap - funcția
findMindetermină elementul cu prioritate minimă - funcțiile
mergeTreesșimergepermit combinarea a două heap-uri.
Găsiți detaliile despre funcționalitate și despre constrângerile de implementare, precum și exemple, direct în schelet. Aveți de completat definițiile care încep cu *** TODO ***.
Pentru rularea testelor, încărcați în interpretor modulul TestBinomialHeap și evaluați main.
Este suficient ca arhiva pentru vmchecker să conțină modulul BinomialHeap.
Etapa 3
În această etapă, veți continua să implementați anumite operații asupra heap-urilor binomiale, în continuarea celor din etapa 2.
Construcțiile și mecanismele noi de limbaj pe care le veți exploata în rezolvare, pe lângă cele din etapa 2, sunt:
- polimorfismul ad-hoc
- clasele.
Ultima operație fundamentală este de eliminare a cheii de prioritate minimă din heap. Am lăsat-o la final, deoarece utilizează operația de combinare (mergeTrees) implementată în etapa 2. Eliminarea presupune înlăturarea primului arbore cu rădăcină de prioritate minimă din lista de arbori ai heap-ului (prin înlocuirea lui cu EmptyTree) și apoi combinarea (mergeTrees) noii liste de arbori cu lista de subarbori (orfani) ai rădăcinii tocmai înlăturate. Având în vedere că lista de arbori ai heap-ului este ordonată crescător în raport cu rangul, iar lista de subarbori orfani este ordonată descrescător (conform structurii arborilor binomiali), este necesară inversarea ultimeia înainte de combinarea celor două liste! Având la bază operația de combinare, rezultă că și cea de eliminare are complexitate logaritmică.
Scheletul etapei 3 se găsește tot în modulul BinomialHeap, în continuarea operațiilor din etapa 2, începând cu linia 243:
- funcția
isolateeste ajutătoare, pregătind terenul pentru următoarea operație - funcția
removeMinînlătură prima cheie de prioritate minimă din heap - instanțele clasei
Showpentru tipurileBinomialTree p kșiBinomialHeap p koferă reprezentări mai lizibile, sub formă de șir de caractere ale celor două categorii de structuri; observați că a fost necesară eliminareaderiving Showdin definiția tipurilor, pentru evitarea conflictului de instanțe - instanțele clasei
Functorpentru constructorii de tipBinomialTree pșiBinomialHeap pgeneralizează funcționalamappe aceste categorii de structuri - pentru bonus, instanța clasei
Foldablepentru constructorul de tipBinomialTree pgenerealizează funcționalafoldrpe aceste structuri.
Găsiți detaliile despre funcționalitate și despre constrângerile de implementare, precum și exemple, direct în schelet. Aveți de completat definițiile care încep cu *** TODO ***.
Pentru rularea testelor, încărcați în interpretor modulul TestBinomialHeap și evaluați main.
Este suficient ca arhiva pentru vmchecker să conțină modulul BinomialHeap. Veți avea nevoie de implementarea funcției mergeTrees din etapa 2.
Precizări
- Încercați să folosiți pe cât posibil funcții predefinite din modulul Data.List. Este foarte posibil ca o funcție de prelucrare de care aveți nevoie să fie deja definită aici.
- Ca sugestie, exploatați cu încredere pattern matching,
caseși gărzi, în locul if-urilor imbricate.
Resurse
Changelog
- 22.04 (ora 16:10) Publicare etapa 2, doar enunț și schelet; urmează și checker-ul.
- 24.04 (ora 22:45) Publicare checker etapa 2.
- 26.04 (ora 10:55) Actualizare checker etapa 2. Și
BinomialHeapinstanțiază acumEqpentru facilitarea noilor teste. - 28.04 (ora 14:50) Actualizare checker etapa 2 pt verificări mai flexibile. Dacă ați încărcat deja etapa 2 pe vmchecker, NU este necesară reîncărcarea.
- 30.04 (ora 10:30) Publicare etapa 3, doar enunț și schelet; urmează și checker-ul.
- 30.04 (ora 22:35) Actualizare checker etapa 2, în urma unor probleme semnalate de voi. Se verifică acum corespondența corectă dintre rangul arborilor și poziția acestora în lista heap-ului.
- 04.05 (ora 10:45) Publicare checker etapa 3.