Introducere

Aceasta lucrare trateaza problema controlului pozitiei unui obiect metalic in camp magnetic. Domeniul levitatiei magnetice a capatat o atentie sporita datorita faptului ca elimina piederile de energie prin frecare in timpul contactului mecanic. Printre aplicatiile levitatiei magnetice se numara trenurile maglev de mare viteza, platforme de pozitionare de mare precizie si navete aerospatiale.

Descriere generala

Sistemul consta dintr-un corp metalic aflat in camp magnetic si in camp gravitational. Datorita celor doua campuri, asupra corpului metalic se exercita doua forte pe aceeasi directie, dar in sensuri opuse: forta magnetica si forta gravitationala. Sistemul descris se va afla in echilibru daca cele doua forte sunt egale in modul.

Campul magnetic necesar obtinerii echilibrului sistemului va fi generat utilizand un electromagnet cu miez feromagnetic. Forta generata de acest camp magnetic este direct proportionala cu intensitatea curentului electric prin electromagnet si invers proportionala cu distanta de la capatul de jos al electromagnetului pana la obiect, constanta de proportionalitate depinzand de constructia electromagnetului.

Modelul matematic ce descrie acest sistem este urmatorul

$\\ m\ddot{x} = F_g - F_m\\ F_g = mg\\ F_m = C\dfrac{i^2(t)}{x^2(t)}\\$

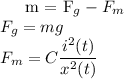
Ceea ce conduce la o ecuatie diferentiala neliniara de ordinul II:

$\\ m\ddot{x} = mg - C\dfrac{i^2(t)}{x^2(t)}\\$

Pentru o pozitie oarecare a obiectului se poate calcula pozitia de echilibru a sistemului:

$\\ mg = C\dfrac{i_{0}^2}{x_{0}^2} \Rightarrow e=(x_0, i_0)\\$

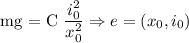
Se considera functia:

$F_{m}(x,\ i) = C\dfrac{i^2}{x^2}\\$

Derivatele ei partiale exista si sunt continue, deci functia este diferentiabila:

$\\ \dfrac{\partial F_{m}}{\partial x} = -2C\dfrac{i^2}{x^3}\\ \dfrac{\partial F_{m}}{\partial i} = 2C\dfrac{i}{x^2}\\ \forall x>0$

Acum se poate liniariza functia in jurul pozitiei de echilibru folosind jacobianul:

$\\ F_m(v) \approx F_m(e) + J_{F_m}(e)(v-e)\\ F_m(x,i) = F_m(x_0,i_0) + \begin{bmatrix}\dfrac{\partial F}{\partial x} & \dfrac{\partial F}{\partial i}} \end{bmatrix} \begin{bmatrix}x-x_0 \\ i-i_0 \end{bmatrix} \\ F_m(x,i) = C\dfrac{i_0^2}{x_0^2} + \begin{bmatrix} -2C\dfrac{i_0^2}{x_0^3} & 2C\dfrac{i_0}{x_0^2} \end{bmatrix} \begin{bmatrix}x-x_0 \\ i-i_0 \end{bmatrix} \\$

$\\ F_m(x,i) = C\dfrac{i_0^2}{x_0^2} -2C\dfrac{i_0^2}{x_0^3}x + 2C\dfrac{i_0^2}{x_0^2} + 2C\dfrac{i_0}{x_0^2}i - 2C\dfrac{i_0^2}{x_0^2}$

$\\ F_m(x,\ i) = C\dfrac{i_0^2}{x_0^2} -2C\dfrac{i_0^2}{x_0^3}x + 2C\dfrac{i_0}{x_0^2}i\\ F_m(x,\ i) = C\dfrac{i_0^2}{x_0^2} - k_1x + k_2i$

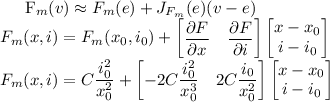
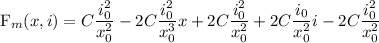
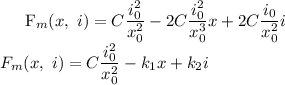
Se inlocuieste in ecuatia diferentiala si se obtine:

$\\ m\ddot{x} = mg - C\dfrac{i_0^2}{x_0^2} + k_1x - k_2i$

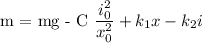
Dar

$\\ mg = C\dfrac{i_0^2}{x_0^2} \Rightarrow m\ddot{x} - k_1x = -k_2i$

Ecuatia ce va descrie sistemul de mai sus in timpul controlului automat este:

$\\ \ddot{x} = \dfrac{k_1}{m}x -\dfrac{k_2}{m}i$

Se fac urmatoarele notatii si se echivaleaza cu sistemul diferential de 2 ecuatii de ordinul I:

$\\ x_1=x,\ x_2=\dot{x}\\ u=i\\ \\ \begin{cases} \dot{x_1} &= x_2 \\ \dot{x_2} &= \dfrac{k_1}{m}x_1 - \dfrac{k_2}{m}u \\ y &= x_1 \end{cases} \\ \\$

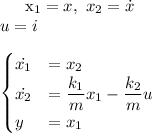
Se aduce la forma standard a unui sistem liniar neted (SLN):

$\\ \begin{cases} \dot{x} &= Ax + Bu \\ y &= c^Tx \\ \end{cases} \\ \\ \\ A=\begin{bmatrix} 0 & 1\\ \dfrac{k_1}{m} & 0 \end{bmatrix},\ B=\begin{bmatrix} 0\\ -\dfrac{k_2}{m} \end{bmatrix},\ c^T=\begin{bmatrix} 1 & 0 \end{bmatrix}$

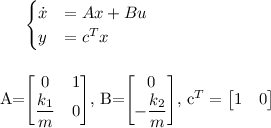
Parametrii procesului sunt:

$\\ m=28 \cdot 10^{-3} \ Kg\\ g=9.8 \ m/s^2\\ C=9.67 \cdot 10^{-7} \ N\left(\dfrac{m}{A}\right)^2\\ x_0=4 \cdot 10^{-3} \ m\\ i_0=2.13 \ A$

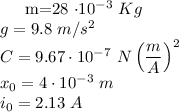
Se pot determina constantele ce apar in matricele sistemului:

$\\ k_1=2C\dfrac{i_0^2}{x_0^3} = 137.2 \\ k_2=2C\dfrac{i_0}{x_0^2} = 0.25 \\ \dfrac{k_1}{m} = 4900 \\ \dfrac{k_2}{m} = 9.2\\ \\ A=\begin{bmatrix} 0 & 1\\ 4900 & 0 \end{bmatrix},\ B=\begin{bmatrix} 0\\ -9.2 \end{bmatrix},\ c^T=\begin{bmatrix} 1 & 0 \end{bmatrix}$

Se determina functia de transfer:

$\\ H(s) = c^T(sI-A)^{-1}B \\ H(s) = \dfrac{-9.2}{s^2-4900}$

Se reprezinta locul Nyquist. Din teorema Nyquist de stabilitate rezulta ca sistemul in bucla inchisa este intern asimptotic instabil.

$\\ (q_{0} + 2N{p})\dfrac{\pi}{2} = \delta \\ q_{0} = 0 \\ N_{p} = 1 \\ \delta = \alpha_{f} - \alpha_{i} \\ \delta = 0 - 0 = 0$

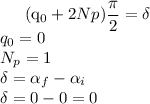
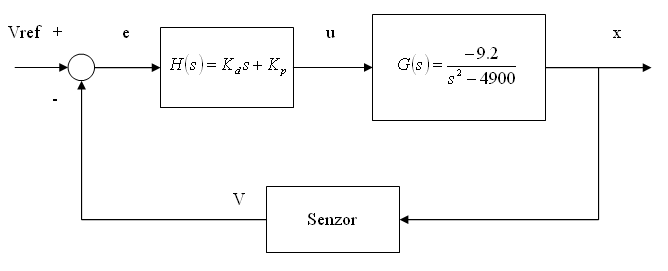
Desi as fi preferat sa stabilizez sistemul din varf de penita, proiectand o lege de comanda prin reactie dupa stare, u=Fx, care sa stabilizeze sistemul, acest lucru nu este posibil deoarece sistemul descris prezinta neliniaritati puternice, constanta electromagnetului a fost determinata experimental si legea de miscare nu se verifica decat in punctul de echilibru. Prin urmare, voi folosi un regulator PD in bucla de reactie, ai carui parametrii pot fi modificati dupa nevoie. Schema bloc a sistemului este:

Functia de transfer a blocului regulator, sistem dinamic este urmatoarea:

$\\ H'(s) = H(s)G(s) \\ H'(s) = \dfrac{-9.2K_{d}s -9.2K_{p}}{s^2-4900}$

Functia de transfer a intregului bloc este:

$\\ H''(s) = \dfrac{H'(s)}{1+H'(s)} \\ H''(s) = \dfrac{-9.2K_ds -9.2K_p}{s^2-9.2K_ds -9.2K_p -4900} \\$

Acum, pentru a stabiliza sistemul, trebuie alese constantele regulatorului astfel incat polii functiei de transfer sa aiba partea reala negativa. Acest lucru se intampla numai daca se aleg constantele negative, respectiv:

$\\ K_p = -600 \\ K_d = -5 \\ H''(s) = \dfrac{46s + 5520}{s^2+46s+620}$

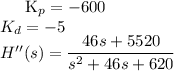
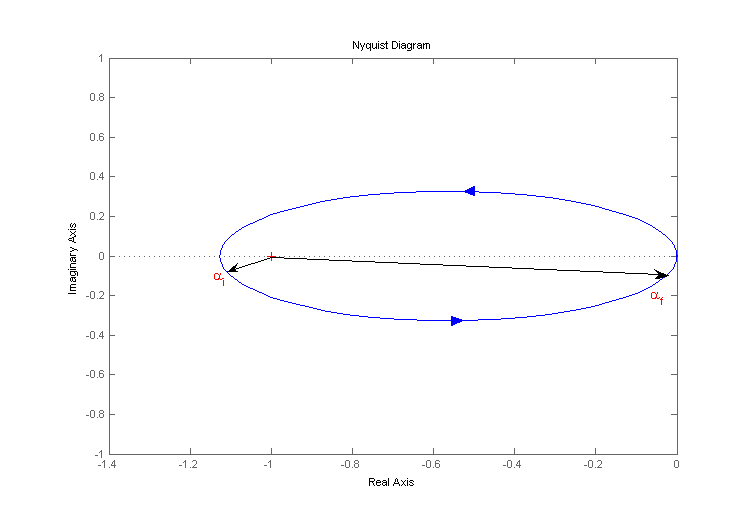
Locul Nyquist pentru functia de transfer in bucla deschisa, H'(s), arata ca in figura de mai jos. Se aplica teorema Nyquist de stabilitate, iar sistemul in bucla inchisa rezulta intern asimptotic stabil.

$\\ (q_{0} + 2N{p})\dfrac{\pi}{2} = \delta \\ q_{0} = 0 \\ N_{p} = 1 \\ \delta = \alpha_{f} - \alpha_{i} \\ \delta = 2\pi - \pi = \pi$

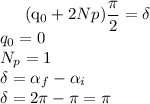
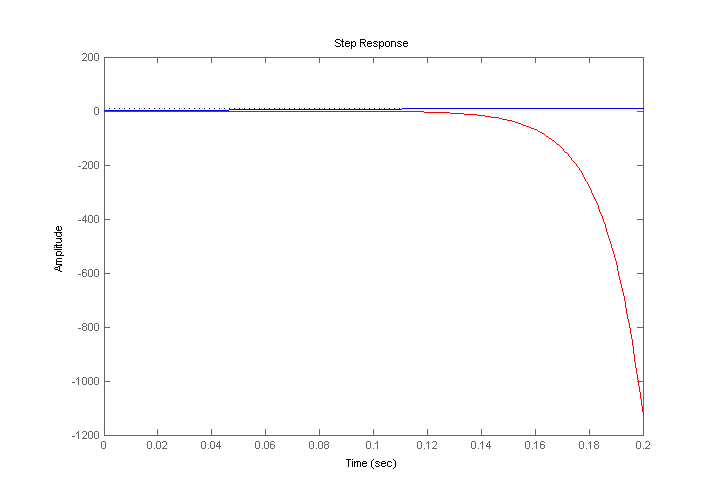
In figura de mai jos este reprezentat raspunsul sistemului la un semnal treapta. Curba reprezentata cu rosu este cea a sitemului fara regulator, in bucla deschisa, iar cea reprezentata cu albastru este a sitemului cu regulator, in bucla inchisa. Se poate observa ca sistemul se stabilizeaza.

Hardware Design

Comanda pentru electromagnet se face cu un Atmega16 folosind Fast PWM prin pinul PD5 de pe portul D. Cu acesta se comanda un tranzistor in clasa D compus dintr-un tranzistor de comutatie BC547C si un tranzistor de putere TIP41C. S-a conectat si o rezistenta la baza tranzistorului TIP41C pentru a-l accelera. Tranzistorul darlington comanda curentul prin electromagnet, diminuand astfel efectul autoinductiei. Pentru a elimina complet acest efect, dar si pentru a proteja circuitul, s-a legat o dioda Schottky la bornele electromagnetului.

La pinul PA0 de pe portul A este legat un traductor optic liniar a carui tensiune este convertita digital de catre modulul de ADC al microcontroller-ului. Acesta este setat pe 10 biti si functioneaza la o frecventa de 250 Khz. Desi traductorul se poate face cu o fotodioda si un amplificator operational, am ales sa folosesc la proiect un TSL 257 care functioneaza in domeniul spectrului vizibil, avand timp de raspuns minim pentru lungimea de unda de 650 nm.

Software Design

Programul de pe microcontroller trebuie sa implementeze algoritmul pentru regulatorul PD. Pentru a face acest lucru, initializez modulul de PWM, convertorul AD si comunicarea seriala pentru a putea seta parametrii regulatorului. Algoritmul pentru regulator este prezentat in continuare, in pseudocod.

Aici se calculeaza eroarea curenta si derivata ei. Se calculeaza iesirea pentru PWM, tinand cont ca trebuie adaugata si o constanta K ce asigura tensiunea pentru pozitia de echilibru in jurul careia se opereaza.

Programul complet este disponibil in link-ul de mai jos. Trebuie mentionat ca am folosit AVR Studio 4 si WinAVR pentru compilare si generare de cod.

  K = 0x3600
  previous_error = 0
  while 1 
      current_error  = Vreference - Vcurrent
      derivative     = current_error - previous_error
      output         = K + Kp*current_error + Kd*derivative
      previous_error = current_error

maglev.zip

Rezultate Obţinute

Sistemul se comporta conform asteptarilor, stabilizandu-se in jurul pozitiei de echilibru. Pentru aceste demonstratii am folosit o bila cu masa destul de mare, pentru echilibru fiind nevoie de un curent mare care sa treaca prin electromagnet. Din aceasta cauza acesta se supraincalzeste, iar curentul prin el scade. Prin urmare, dupa 10s sistemul devine instabil, iar bila scapa de sub controlul campului electromagnetic.

Mai jos am pus cateva clipuri video si poze.

http://www.youtube.com/watch?v=9SK2Agmx9MA

http://www.youtube.com/watch?v=tYcMNMNmXAA

Concluzii

Problema prezentata este una complexa, dar care merita studiata. Proiectul ar putea fi dezvoltat pe viitor pentru a realiza o statie de pozitionare foarte precisa, ce poate fi controlata de la calculator. Pentru aceasta este nevoie de un sistem mai performant, determinarea relatiilor dintre parametrii regulatorului, pozitia obiectului si tensiunea furnizata de senzor. Chiar si acum se poate deplasa obiectul pe verticala, cu o precizie foarte mare, dar in limitele stabilitatii.

Multumesc indrumatorului de proiect Razvan Tataroiu pentru ajutorul acordat in realizarea acestei lucrari in ceea ce priveste proiectarea circuitului de comanda pentru electromagnet.