Table of Contents

Lab 02 - Cryptography

Objectives

Resources

Preparation

You may use the UPB's OpenStack cloud to instantiate a Virtual Machine to be used for this lab! Read these instructions if you wanna know how!.

Overview

Cryptography refers to the technique of securing information and communications through use of codes, especially to prevent unauthorised access.

There are two main types:

Symmetric Key Encryption

Symmetric-key encryption is based on either stream ciphers or block ciphers.

Block ciphers have one or more block size(s) but, during transformation, the block size is always fixed. Block cipher modes operate on whole blocks and require that the last part of the data be padded to a full block if it is smaller than the current block size. There are, however, modes that do not require padding because they effectively use a block cipher as a stream cipher; such ciphers are capable of encrypting arbitrarily long sequences of bytes or bits.

Most block cipher modes require a unique binary sequence, often called an initialization vector (IV), for each encryption operation. The IV has to be non-repeating and, for some modes, random as well. The initialization vector is used to ensure distinct ciphertexts are produced even when the same plaintext is encrypted multiple times independently with the same key.

The simplest of the encryption modes is the ECB (Electronic Codebook) mode. The message is divided into blocks, and each block is encrypted separately (with the same key and no IV). The disadvantage of this method is that identical plaintext blocks are encrypted into identical ciphertext blocks, so statistical analysis can reveal the protected message:

In CBC (Cipher Block Chaining) mode, each block of plaintext is XORed with the previous ciphertext block before being encrypted. This way, each ciphertext block depends on all plaintext blocks processed up to that point. To make each message unique, a random initialization vector must be used in for first block.

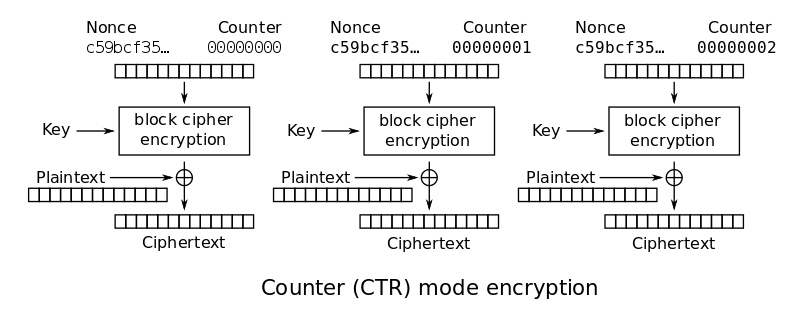
There is also a CTR (Counter) mode that specifically turns the block algorithm into a stream cipher: a keystream is generated by encrypting a random IV (i.e. nonce) with the key for the first block and, for successive fragments, the IV is incremented (any deterministic function can be used) and encrypted with the same key. The plaintext is XOR-ed with the keystream (basic stream cipher operation) thus the ciphertext is obtained.

Asymmetric Encryption, RSA

Public-key cryptography uses two separate keys, one for encryption (the public key) and one for decryption (the private key). Anyone with the public key can compute an encrypted message that only the owner of the private key can read.

RSA was the first algorithm that demonstrated this concept. Its security assumptions are based on complexity theory: computing the product of two prime numbers is easy (polynomial time), but there is no efficient algorithm for factoring them back (so far, all factorization methods are in the non-polynomial class).

The keys for the RSA algorithm are generated the following way:

  1. Choose two different large random prime numbers p and q
  2. Calculate n = pq
    • n is the modulus for the public key and the private keys
  3. Calculate the totient: phi (n)=(p-1)(q-1).
  4. Choose an integer e such that 1 < e < phi(n), and e is coprime to phi(n)
    • e is released as the public key exponent
  5. Compute d to satisfy the congruence relation d*e ≡ 1 (mod(phi(n)))
    • d is kept as the private key exponent

The public key is made of the modulus n and the public (or encryption) exponent e.

The private key is made of the modulus n and the private (or decryption) exponent d which must be kept secret.

Encrypting a message: c = m ^ e (mod n)

Decrypting a message: m = c ^ d (mod n)

Example: 

p = 29, q = 31
n = p * q = 29 * 31 = 899
phi = (p -1) * (q – 1) = (29 – 1) * (31 – 1) = 840
e = 11
d * e ≡ 1 mod phi => (d * 11) / phi will give us a remainder of one.
(611 * 11) = 6721 and 6721 / 840 = 8 with remainder 1 => d = 611
C = M ^ e mod n
C = 119 ^ 11 mod 899 = 595
M = C ^ d mod n
M = 595 ^ 611 mod 899 = 119

In this case “^” means exponentiation (raise to power), not XOR

Exercises

0. [5p] AES ECB (Warmup)

It is recommended NOT to encrypt more than one block with AES in ECB mode, but in order to understand why, an image with the following header was encrypted. The encrypted photo cand be found here (.zip). Is it possible to figure out what the initial image was? 

42 4D 66 CA D7 00 00 00 00 00 36 00 00 00 28 00 00 00 D0 07 00 00 35 09 00 00 01 00 18 00 00 00 00 00 30 CA D7 00 74 12 00 00 74 12 00 00 00 00 00 00 00 00 00 00

1. [20p] AES

This file (compressed as .zip) was encrypted using the following code. Can you decrypt it? 

from Crypto.Cipher import AES
from Crypto import Random
 
BLOCK_SIZE = 32
PADDING = b'#'
iv = b"\x00" * 16
 
def encrypt(key, iv, data):
    aes = AES.new(key, AES.MODE_CBC, iv)
    data = aes.encrypt(data)
    return data
 
def pad(s):
    return s + (BLOCK_SIZE - len(s) % BLOCK_SIZE) * PADDING 
 
 
key = Random.new().read(BLOCK_SIZE)
 
with open('plain.jpg', 'rb') as f:
    data = f.read()
 
enc = encrypt(key, iv, pad(data))
 
f_out = open("secret.enc", 'wb')
f_out.write(key)
f_out.write(enc)
f_out.close()

You might need to install pycryptodome: 

pip3 install pycryptodome

2. [20p] RSA - Known factorisation

In order to decrypt the ciphertext, you need to factorize n into p and q, compute phi and find d. 

c = 28822365203577929536184039125870638440692316100772583657817939349051546473185
n = 70736025239265239976315088690174594021646654881626421461009089480870633400973
e = 3
sudo apt-get install python3-gmpy2  # or python-gmpy2, depending on your Python version
print(hex(message)[2:].decode("hex"))  # python 2
print(bytearray.fromhex(hex(message)[2:]))  # python 3

Useful gmpy2 functions:

03 [15p] Is this even OTP?

04 [20p] Many Time Pad

05 [20p] We want Jokes instead of Nukes

If you find this cringe, just wait until you see the assignments! ;)

6. [10p] Feedback

Please take a minute to fill in the feedback form for this lab.