Table of Contents
10. LLVM Passes - code analysis
Analiza fluxului de date oferă informație globală despre modul în care o procedură sau, în general, un segment de program manipulează datele.
Un exemplu de optimizare ce se poate realiza cu o analiză a fluxului de date este propagarea constantelor:
- se identifică toate atribuirile prin care o variabilă primește ca valoare o constantă
- se determină, pentru fiecare punct din program în care este folosită o variabilă, câte și care dintre atribuirile acelei variabile la o constantă sunt vizibile în acel punct
- dacă toate atribuirile vizibile în acel punct atribuie aceeași constantă variabilei, atunci folosirea variabilei se poate înlocui cu acea constantă
Pentru ca un analizor să poată emite astfel de judecăți asupra programului analizat trebuie să mențină pentru fiecare punct de interes din programul analizat (de obicei pentru fiecare intrare sau ieșire dintr-un basic block) o structură de date cu informații despre cum sunt manipulate datele. În cele ce urmează vom prezenta modelul matematic folosit cel mai des pentru reprezentarea acestei informații precum și un algoritm iterativ de analiză a fluxului de date.
Cadrul conceptual
Analiza fluxului de date se realizează prin executarea de operații asupra unei structuri algebrice denumită latice. Elementele laticei reprezintă proprietăti abstracte ale variabilelor, expresiilor sau altor componente din program. Fiecărei portiuni de interes din program (instrucțiune, basic block sau procedură) i se asociază un element de latice care memorează proprietățile urmărite de analiză pentru respectiva porțiune.
Aceste proprietăți se referă la toate execuțiile posibile în cadrul unei proceduri (dacă vorbim de analiza intra-procedurală), fără a ține seama de datele de intrare și de drumurile în graful fluxului de control al procedurii. Mai precis, cele mai multe metode de analiză de date nu țin cont dacă o condiție este îndeplinită sau nu (cu alte cuvinte care din ramuri este executată) sau de câte ori se execută o buclă. Totuși, informațiile cu care operează analiza vor fi conservative (de exemplu, se poate presupune ca ambele ramuri ale unei conditii pot fi executate) pentru ca să nu se tragă concluzii greșite asupra programului (care ar putea duce la efectuarea unor transformări/optimizări care să facă programul incorect).
Pentru a modela efectul pe care îl are fiecare componentă a programului asupra elementelor de latice, se defineste o așa numită funcție de flux. Se asociază câte o funcție de flux fiecărei porțiuni de interes (instrucțiune, basic block sau procedură). Spre exemplu, o funcție de flux asociată unei instructiuni primește ca parametru un element de latice și întoarce elementul de latice transformat în urma execuției instrucțiunii respective. O funcție de flux asociată unui bloc de bază are ca intrare tot un element de latice și întoarce elementul de latice așa cum este el transformat în urma execuției blocului respectiv. De obicei, funcția de flux asociată unui basic block este rezultată din compunerea funcțiilor de flux asociate instrucțiunilor din bloc.
Propietăți importante
În general, o latice L este formată dintr-o mulțime de valori și două operații pe care le vom nota ∩ (meet) și ∪ (join) care au următoarele proprietăți:
- închidere - ∀x ∈ L, ∀y ∈ L ∃z ∈ L și ∃w ∈ L unici, astfel încât x ∩ y = z și x ∪ y = w
- comutativitate - orice x, y ∈ L, x ∩ y = y ∩ x si x ∪ y = y ∪ x
- asociativitate - orice x, y, z ∈ L, (x ∩ y) ∩ z = x ∩ (y ∩ z) și (x ∪ y) ∪ z = x ∪ (y ∪ z)
- absorbție - orice x, y ∈ L, (x ∩ y) ∪ y = y si (x ∪ y) ∩ x = x
- existenei și unicitatea elementelor de minim și maxim - min (notat ⊥) și max (notat T), astfel încât ∀x ∈ L, x ∩ ⊥ = ⊥ și x ∪ T = T
- distributivitate - numeroase latici sunt
distributive- ∀x ∈ L, ∀y ∈ L, ∀z ∈ L, (x ∩ y) ∪ z = (x ∪ z) ∩ (y ∪ z) și (x ∪ y) ∩ z = (x ∩ z) ∪ (y ∩ z)
Exemplu de latice
Următorul tip de latice este foarte des folosit:
- elemente constituente - vectori de biți
- operațiile de bază
- meet - AND pe biți
- join - OR pe biți
- elementul ⊥ - vectorul de biți în care toti biții sunt 0
- elementul T - vectorul în care toți biții sunt 1.
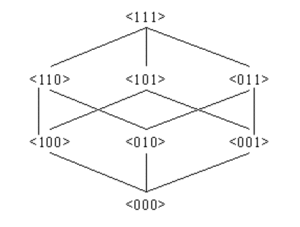
Folosim notatia BVn pentru a desemna o latice de vectori de biți de lungime n. Figura de mai jos contine o prezentare grafica a laticei BV3
Relația de incluziune
Relația de incluziune(notată cu ⊆) este o relație de ordine parțială pe elementele laticei. Aceasta poate fi definită folosind operatia ∩ astfel: x ⊆ y ⇔ x ∩ y = x. Se poate da și o definiție duală folosind operatia ∪. Următoarele proprietăți ale relației ⊆ se demonstrează cu ușurință pe baza proprietăților operațiilor ∪ și ∩:
- reflexivitate - ∀x ∈ L, x ⊆ x
- antisimetrie - ∀x ∈ L, ∀y ∈ L, dacă x ⊆ y și y ⊆ x atunci x = y
- tranzitivitate - ∀x ∈ L, ∀y ∈ L, ∀z ∈ L, dacă x ⊆ y și y ⊆ z, atunci x ⊆ y
În mod corespunzator se definesc și relatiile ⊂, ⊃, ⊇.
Monotonia funcțiilor de flux
O funcție de flux ce mapează laticea pe ea însăși (f : L → L) este monotonă dacă ∀x ∈ L, ∀y ∈ L, x ⊆ y ⇒ f(x) ⊆ f(y). De exemplu, funcția f : BV3 → BV3 definită prin f(<x1x2x3>) = <x11x3> este monotonă.
Înălțimea unei latice este lungimea celui mai lung lanț strict crescător din latice, adică cel mai mare n astfel încât ⊥ = x1 ⊂ x2 ⊂ … ⊂ xn = T. De exemplu, înălțimea laticei BV3 din figura de mai sus este 4.
Pentru o problemă particulară de analiză a fluxului de date, o funcție de flux modelează efectul unei porțiuni de interes. Pentru a putea rezolva o problemă de analiză de flux de date impunem ca toate funcțiile de flux să fie monotone. Acest lucru este rezonabil ținând cont că scopul unei funcții de flux este să modeleze informația (despre problema de flux de date) oferită de o porțiune de program și, deci, nu ar trebui să scadă cantitatea de informație deja obținută. Monotonia este de asemenea esențială pentru a demonstra că algoritmii de analiză a fluxului de date se termină și pentru a calcula complexitatea lor.
Fiind dat un set de ecuații de flux de date, valoarea pe care vrem să o calculăm este așa-numita soluție “meet-over-all-paths” (MOP).Fie:
G = <N, E>- CFG (control flow graph)Path(B)- mulțimea tuturor căilor de la bloculentryla B cu B ∈ Np- o cale oarecare din Path(B)FB- funcția de flux reprezentând fluxul prin blocul BFp- compunerea funcțiilor de flux întâlnite pe calea p- dacă
B1 = entry, …, Bn = Bsunt blocurile ce constituie caleap, atunciFP = FBn o … o FB1 init- valoarea din latice asociata cu bloculentry
Atunci, solutia MOP este: $MOP(B) = \sqcap_{p\in\mathbf{Path(B)}}{F_p(Init)}$, relația fiind aplicată pentru entry, B1, … , Bn, exit.
Clasificarea problemelor de analiză a fluxului de date
Problemele de analiză de date se clasifică după urmatoarele criterii:
- informația pe care trebuie să o ofere
- atributele urmărite (relaționale sau independente)
- tipurile de latice folosite, semnificațiile elementelor de latice și funcțiile definite pe acestea
- direcția fluxului de informație:
- probleme de tip “înainte” - în direcția execuției programului
- probleme de tip “înapoi” - în direcția opusă execuției programului
- probleme “bidirecționale” - în ambele direcții
Toate problemele pe care le tratăm aici sunt probleme cu atribute independente (atribuie un element al laticei fiecarui obiect de interes – de exemplu definire de variabilă, calcul de expresie etc.). Problemele relaționale au o complexitate computațională mult mai mare decât cele cu atribute independente. Similar, aproape toate problemele pe care le tratăm sunt unidirecționale (de tip înainte sau de tip înapoi). Problemele bidirecționale impun propagarea informației și înainte, și înapoi în acelasi timp și sunt mult mai complicat de formulat, înteles și rezolvat decât cele unidirecționale.
Tipuri de probleme
Tipuri importante probleme de analiza fluxului de date:
- Vizibilitatea definirilor (reaching definitions) - găsirea definirilor unei variabile (adică locurile unde acelei variabile îi este atribuită o valoare) care ajung să fie utilizate la un anumit punct în procedură. De exemplu:
a = 5 // definirea #1 printf(a); // definirea #1 este utilizata aici if (b > c) a = 10; // definirea #2 return a; // ambele definiri pot fi utilizate aici
. Aceasta este o problema de tip înainte, care folosește o latice de vectori de biți în care fiecare bit corespunde unei definiri a unei variabile.
- Folosirile expuse (exposed uses) - este problema duală celei de mai sus - pentru fiecare punct al programului în care este definită o variabilă se determină ce folosiri ale variabilei pot utiliza acea definire (sunt expuse acelei definiri). Este o problema de tip înapoi și folosește o latice de vectori de biți, în care fiecarui bit îi este asociată o folosire a unei variabile.
- Expresiile disponibile (available expressions) - determinarea expresiilor disponibile în fiecare punct din procedură, în sensul că pe orice cale, de la intrarea în procedură până în acel punct, are loc o evaluare a expresiei și nici una din variabilele folosite în expresie nu primește o valoare nouă între ultima evaluare a expresiei și respectivul punct din program. Aceasta este o problema de tip înainte care folosește o latice de vectori de biți în care fiecare bit este asociat unei definiri a unei expresii.
- Variabilele în viață (live variables) - determinarea pentru o anumită variabilă și un anumit punct din program dacă mai există o folosire a valorii variabile până la ieșirea din procedură. Aceasta este o problema de tip înapoi și elementul de latice este un vector de biti în care fiecare bit este asociat unei variabile.
- Propagarea copierilor (copy propagation) - determinarea dacă pe fiecare cale de la o copiere a unei variabile x ← y la o folosire a variabilei x, valoarea lui y rămâne neschimbată. Aceasta este o problema de tip înainte care folosește vectori de biți, iar fiecare bit reprezintă o copiere a unei variabile.
- Propagarea constantelor (constant propagation) - determinarea valorii unei variabile într-un anumit punct, dacă aceasta valoare este constantă. Problema e de tip înainte și nu folosește o latice de vectori de biți.
- Analiza parțială a redundanței (partial redundancy) - determinarea calculelor care se efectuează de mai multe ori pe o anumită cale de execuție, fără ca operanzii să se fi modificat între timp. De asemenea se determină și definirile redundante (nefolosite) ale unei variabile. Problema este de tip bidirecțional și folosește vectori de biți în care fiecare poziție reprezintă o calculare a expresiei.
Problemele de mai sus nu sunt singurele de analiză de date, dar sunt dintre cele mai importante. Există mai multe abordări în rezolvarea problemelor de flux de date. Aici vom descrie algoritmul iterativ al lui Kildall.
Analiza iterativă a fluxului de date - Algoritmul lui Kildall
În continuare vom prezenta metoda iterativă de analiză a fluxului de date, întrucât este cel mai simplu de implementat și, ca urmare, cel mai frecvent folosită. Vom avea în vedere analiza de tip înainte. Problemele de tip înapoi reprezintă o simplă adaptare a metodei.
Pentru un CFG, G = <N, E> unde entry și exit sunt blocuri în N, se dorește să se calculeze:
- in(B) ∈ L, ∀B ∈ N - informația despre fluxul de date la intrarea în blocul B
- $in(B) = \left\{\begin{array}{ll} Init & \mbox{ daca } B = entry \\ \sqcap_{p\in\mathbf{pred(B)}}{out(p)} & \mbox{ altfel } \end{array} \right.$
- out(B) ∈ L, ∀B ∈ N - informația despre fluxul de date la ieșirea din blocul B
- $out(B) = F_{B}(in(B))$
unde:
Init- valoarea inițială pentru informația despre fluxul de date la intrarea în procedurăFB()- transformarea asupra informației de flux de date corespunzătoare executării bloculuiB- $\sqcap$ - modelează efectul combinării informației de flux de date de pe arcele care intră într-un bloc.
În funcție de problemă, efectul combinării informației de flux de date de pe arcele care intră într-un bloc poate fi modelat de ∪ sau de ∩. Analog, valoarea lui Init poate fi ⊥ sau T. Ecuațiile pot fi exprimate doar în funcție de in(B) astfel:
$$in(B) = \left\{\begin{array}{ll} Init & \mbox{ daca } B = entry \\ \sqcap_{p\in\mathbf{pred(B)}}{F_{p}(in(p))} & \mbox{ altfel } \end{array} \right.$$
Algoritmul AnalizaIterativa foloseste doar informații in(). Strategia acestuia este aceea de a aplica în mod iterativ ecuațiile date mai sus și de a menține o listă de blocuri pentru care valorile in() s-au schimbat la ultima iterație, până când se golește lista.
Inițializări:
- lista conține toate blocurile din CFG, exceptând blocul
entry, deoarece informația acestuia nu se schimbă niciodată. totalEffecteste inițializat cu T pentru că am considerat că ∩ modelează efectul combinării informației de flux de date de pe arcele care intră într-un nod.
procedure AnalizaIterativa(N, entry, F, Init, in) N: in set of Node entry: in Node F: in (Node x L) -> L Init: in L in: out Node -> L begin B, P: Node nodeList: set of Node totalEffect: L in(entry) = Init nodeList = N - {entry} for each B ∈ N do in(B) = T done repeat B = an element from nodeList nodeList = nodeList - {B} totalEffect = T for each p ∈ pred(B) do totalEffect = totalEffect ∩ Fp(in(p)) done if (in(B) != totalEffect) then in(B) = totalEffect nodeList = nodeList ∪ succ(B) fi until nodeList = ∅ end
Eficiența computațională a algoritmului depinde de câțiva factori:
- dimensiunea laticei
- funcțiile de flux
FB - felul în care se administrează lista de blocuri
Primii doi factori depind de problemă, în timp ce felul în care este administrată lista este independent de problemă.
Cea mai simplă implementare este aceea în care se folosește o stivă sau o coadă, fără a ține seama de relațiile dintre blocuri (arcele din CFG). Pe de altă parte, însă, dacă se procesează toți predecesorii unui bloc înaintea prelucrarii acestuia, atunci se va obține efect maxim asupra informației blocului de fiecare dată când este întâlnit. Pot fi astfel de rezultate dacă, de exemplu, lista va fi completată în ordine inversa printr-o parcurgere postordine și se va opera apoi asupra ei precum asupra unei structuri de date de tip coadă. În acest context, dacă A este numarul maxim de arce înapoi pe oricare drum aciclic din CFG, atunci A+2 iteratii prin bucla repeat vor fi suficiente pentru terminarea algoritmului. În practică este A ≤ 3 și, cel mai frecvent, A = 1.
Exemple
Vizibilitatea definirilor (reaching definitions)
| Pseudocod | CFG |
|---|---|
1 receive m 2 f0 <- 0 3 f1 <- 1 4 if m <= 1 goto L3 5 i <- 2 6 L1: if i <= m goto L2 7 return f2 8 L2: f2 <- f0+f1 9 f0 <- f1 10 f1 <- f2 11 i <- i+1 12 goto L1 13 L3: return m |  |
In tabelul de mai jos sunt prezentate corespondența dintre pozițiile biților în cadrul vectorilor, definirea variabilei și blocul în care aceasta are loc.
| Poziția bitului | Definirea | Basic block |
|---|---|---|
| 1 | m din instrucțiunea 1 | B1 |
| 2 | f0 din instrucțiunea 2 | B1 |
| 3 | f1 din instrucțiunea 3 | B1 |
| 4 | i din instrucțiunea 5 | B3 |
| 5 | f2 din instrucțiunea 8 | B6 |
| 6 | f0 din instrucțiunea 9 | B6 |
| 7 | f1 din instrucțiunea 10 | B6 |
| 8 | i din instrucțiunea 11 | B6 |
Funcțiile de flux pentru fiecare bloc sunt prezentate în tabelul de mai jos (id este funcția identitate). La aceste funcții se ajunge relativ ușor folosind seturi kill/gen și explicația procedeului constituie primul exercițiu din acest laborator.
| Funcția asociată unui bloc | Valoarea funcției |
|---|---|
| Fentry | id |
| FB1(<x1 x2 x3 x4 x5 x6 x7 x8>) | <1 1 1 x4 x5 0 0 x8> |
| FB2 | id |
| FB3(<x1 x2 x3 x4 x5 x6 x7 x8>) | <x1 x2 x3 1 x5 x6 x7 0> |
| FB4 | id |
| FB5 | id |
| FB6(<x1 x2 x3 x4 x5 x6 x7 x8>) | <x1 0 0 0 1 1 1 1> |
Valoarea inițială pentru in(B) pentru toate blocurile este <00000000>. Operatorul de combinare a efectelor de pe arcele care intră într-un bloc este U (în acest caz operatorul SAU aplicat pe vectori de biți).
Pași algoritm
| Pas | Operații | Lista de blocuri rezultată |
|---|---|---|
| 1 | Inițializare | {B1,B2,B3,B4,B5,B6,exit} |
| 2 | La intrarea în bucla repeat, valoarea inițiala a lui B este B1.Singurul predecesor al lui B1 este p = entry și rezultatul calculării lui totalEffect este <00000000>, neschimbat față de valoarea inițială a lui in(B1), deci succesorii lui B1 nu sunt adăugați în listă. | {B2,B3,B4,B5,B6,exit} → {B2,B3,B4,B5,B6,exit} |
| 3 | Se ia B = B2. Singurul predecesor al lui B2 este p = B1 și rezultatul calculării lui totalEffect este <11100000>, care devine noua valoare a lui in(B2), deci în lista de lucru se adaugă prin reuniune lista succesorilor lui B2 - {exit}. | {B3,B4,B5,B6,exit} → {B3,B4,B5,B6,exit} |
| 4 | Se ia B = B3. B3 are un singur predecesor, și anume B1, iar rezultatul calculării lui totalEffect este <11100000>, care devine noua valoare a lui in(B3). În lista de lucru se adaugă prin reuniune succesorii lui B3. | {B4,B5,B6,exit} → {B4,B5,B6,exit} |
| 5 | Se ia B = B4. B4 are doi predecesori, B3 si B6. B3 contribuie cu valoarea <11110000>, B6 contribuie cu <00001111> și totalEffect va fi <11111111>, altul decât valoarea anterioară a lui in(B4). În lista de lucru se adaugă succesorii lui B4, B5 și B6 care sunt deja în lista și aceasta rămâne nemodificată. | {B5,B6,exit} → {B5,B6,exit} |
| 6 | Se continuă cu B = B5. B5 are un singur predecesor, anume B4 care contribuie cu valoarea <11111111> la calcularea lui totalEffect, valoare diferită de vechiul in(B5), deci unicul succesor, exit, se adaugă în listă. | {B6,exit} → {B6,exit} |
| 7 | Urmează B = B6. B4, singurul predecesor al lui B6, contribuie cu valoarea <11111111> la calcularea lui totalEffect. in(B6) este modificat și succesorii lui B6 se adaugă la sfârșitul listei. | {exit} → {exit, B4} |
| 8 | Apoi B = exit. Predecesorii lui, B2 si B5 fac ca in(exit) sa devina <1111111>. Acesta nu mai are succesori. | {B4} → {B4} |
| 9 | Apoi se ia din nou B = B4. În acest moment in(B4) = <11111111>. B4 are doi predecesori, B3 si B6. Efectul lui B3 este <11110000> iar al lui B6 este <10001111>, deoarece, între timp, in(B6) a devenit <11111111>. TotalEffect se calculează prin SAU pe biți și rămâne <11111111>, deci in(B4) nu s-a modificat în acestă iterație și nu se va mai adăuga nici un nod în listă. Lista de lucru devine vidă si algoritmul se termină. | {} → {} |
Comentarii algoritm
Algoritmul prezentat aici se poate modifica și folosi foarte simplu și pentru o problemă de tip înapoi, bine formulată. Trebuie ales între a asocia informația de flux de date pentru o astfel de problemă fie cu punctul de intrare, fie cu cel de ieșire al fiecărui bloc. Pentru a folosi dualitatea dintre cele doua tipuri problemele, se optează pentru a doua variantă.
Ca și în problemele de tip înainte, există graful G = <N, E> cu blocurile entry și exit în N și se dorește să se calculeze out(B) ∈ L ∀B ∈ N, unde out(B) reprezintă informația de flux de date la ieșirea din B, exprimată astfel de ecuațiile de flux de date:
- $out(B) = \left\{\begin{array}{ll} Init & \mbox{ daca } B = exit \\ \sqcap_{s\in\mathbf{succ(B)}}{in(s)} & \mbox{ altfel } \end{array} \right.$
- $in(B) = F_{B}(out(B))$
Semnificațiile notațiilor rămân aceleași ca și la problemele de tip înainte. De asemenea, ecuațiile pot fi exprimate doar în funcție de out(B), la fel de ușor. În aceste conditii, algoritmul iterativ pentru probleme de tip înapoi este identic cu cel pentru probleme de tip înainte prezentat mai sus, dacă se fac înlocuirile:
out()devinein()exitdevineentrysucc()devinepred()
Propagarea constantelor (constant propagation)
Propagarea constantelor este utilă pentru detectarea variabilelor cu valori constante în anumite puncte din program. Aceste variabile pot fi înlocuite și pot duce la formarea unor operații ale căror operazi sunt constanți. De aceea, este folosită împreună cu împachetarea constantelor (constant folding).
Următorul exemplu (preluat de pe Wikipedia) este utilizat pentru evidențierea modului de funcționare ale acestor două analize:
| Înainte de optimiazări | După o aplicare a optimizărilor | După a doua aplicare a optimizărilor |
|---|---|---|
int a = 30; int b = 9 - a / 5; int c; c = b * 4; if (c > 10) { c = c - 10; } return c * (60 / a); | int a = 30; int b = 3; int c; c = b * 4; if (c > 10) { c = c - 10; } return c * 2; | int a = 30; int b = 3; int c; c = 12; if (12 > 10) { c = 2; } return c * 2; |
Efectul celor două analize se termină aici. Dacă la “optimization spaghetti”-ul obținut se mai adaugă eliminarea codului mort și detecția faptului că if-ul întotdeuna merge pe calea true, se ajunge (eventual în mai mulți pași) la:
return 4;
Așadar, analizele de propagare și împachetare a constatelor sunt utile, mai ales aplicate împreună cu alte optimizări. Deși se pot implementa aceste două analize folosind reaching definitions și simularea evaluării expresiilor constante în mod iterativ, se propune să se proiecteze un algoritm de tip Kildall care sa le facă pe amândouă în același timp fără a folosi alte informații.
Latice
Pentru asta se definește laticea în următorul mod: pentru fiecare instrucțiune I se definesc seturile in(I) și out(I) care conțin valori pentru toate variabilele vizibile.
O variabilă poate avea una din următoarele valori:
- T - semnifică faptul ca variabila poate fi constantă
- Ci - variabila are valoarea constantă Ci (true, false, 1, -2 etc.)
- ⊥ - variabila sigur nu e constantă
Analiza se va face la nivel de instrucțiune și va fi de tip înainte (se poate adapta analiza la nivel de bloc). Funcția de flux pentru o instrucțiune ce nu este definită va fi funcția identitate: out(I) = in(I). Pentru o definire de forma v1 = v2 op v3, funcția de flux este descrisă de urmatoarele relații:
pentru i != 1 out(I, vi) = in(I, vi)
dacă in(I, v2) și in(I, v3) sunt ambele constante atunci
out(I, v1) = in(I, v2) op in(I, v3)
altfel dacă unul din in(I, v2) sau in(I, v3) este ⊥ atunci
out(I, v1) = ⊥
altfel
out(I, v1) = T
Următorul pas este să se stabilească cum se transferă informația de la o instrucțiune la alta prin CFG (operatorul meet). Cazul instrucțiunilor cu un singur predecesor este trivial: in(I) = out(P). Când există mai mulți predecesori se ține seama de următoarele relații ce descriu operatorul $\sqcap$ (meet). Relațiile sunt date pentru doi operanzi, dar sunt ușor extensibile la mai mulți (în caz că există mai mult de doi predecesori):
- $any \sqcap \top = any$
- $any \sqcap \perp = \perp$
- $C_i \sqcap C_i = C_i$
- $C_i \sqcap C_j = \perp$
De menționat că any, după cum îi spune și numele, poate fi oricare din valori (inclusiv T și ⊥). Pentru a avea algoritmul specificat complet, mai trebuie stabilit cu ce sunt inițializate valorile din latice la începutul algoritmului: in(I, vi) = T, având semnificația “la inceput toate variabilele sunt posibil constante”.
În loc de încheiere
Există o gamă largă de modalități de rezolvare a problemei analizei de date – de la executarea abstractă a unei proceduri care ar putea determina, de exemplu, că aceasta calculează funcția factorial, până la abordări mai simple, ca cea descrisă aici. În toate cazurile, însă, trebuie avută în vedere corectitudinea informației date de analiza fluxului de date, astfel că aceasta să nu reprezinte în mod greșit modul în care procedura analizată acționează asupra fluxului de date. Trebuie avut grijă să se garanteze că transformarile de cod care se bazează pe analiza de date nu iau decizii incorecte din cauza unor greșeli în proiectarea ecuațiilor de flux de date. Astfel, soluțiile acestor ecuații sunt, dacă nu o reprezentare exactă a modului în care procedura își manipulează datele, atunci, cel puțin, o aproximare conservativă a acesteia.
Exerciții de laborator (10p)
Arhiva laboratorului.
Indicatii:
- clasa Instruction este subclasă a
Mai jos este un exemplu de instrucțiune (Instruction). Ea este şi utilizator (User) ale variabilelor (Value) a şi b. În acelaşi timp reprezintă şi definirea variabilei (Value) c.
%c = add i32 %a, %b
Aici este un exemplu de cum pot fi parcurşi toţi utilizatorii unei variabile.
Aici este un exemplu de cum pot fi parcurse toate basic block-urile dintr-o funcţie.
Aici este un exemplu de cum pot fi parcurse toate instrucţiunile dintr-un basic block.
Aici este un exemplu de cum pot fi parcurse toate instrucţiunile dintr-o funcţie.
Aici este un exemplu de cum pot fi parcurşi toţi predecesorii şi succesorii unui basic block.
Aici este un exemplu de cast folosit la exerciţiul 2.
Aici este o scurtă descriere a structurii de date ValueMap folosită la exerciţiul 2.
Aici este o scurtă descriere a structurii de date BitVector folosită la exerciţiul 2.
Exercițiul 1
“Dead Code Elimination” este o optimizare prin care se elimină instrucțiunile al căror rezultat nu influențeaza rezultatul final al programului. Analiza fluxului de date poate oferi informații utile pentru detectarea acestor instrucțiuni. În LLVM sunt implementate mai multe pass-uri ce pot elimina astfel de instrucțiuni, de ex: -die, -dse, -dce sau -adce.
- Compilați fișierul test.c de la sfârșitul exercițiului și aplicați pe rând pass-urile “dce” și “adce”. Care e diferența dintre cele două optimizări? De ce “dce” nu reușește să elimine toate instrucțiunile (ex cele din for.body)?
clang -c -O0 -emit-llvm test.c -c -o test.bc opt -p -mem2reg -dce < test.bc > /dev/null opt -p -mem2reg -adce < test.bc > /dev/null
- Analizați implementările celor două pass-uri (
DCE.cpp,ADCE.cpp) pentru a observa diferențele. Găsiți sursele în subdirectorul~/llvm-3.6.2/src/lib/Transforms/Scalardin locația în care ați instalat llvm.
- Pentru a întelege mai bine limitările primului pass, modificați
DCE.cppastfel încât să afișeze lista instrucțiunilor care folosesc instrucțiunea curentă (def-use chain) la fiecare iterație prin WorkList (while (!WorkList.empty())).- Pentru modificarea pass-ului, copiați sursa
DCE.cppîntr-un pass custom (ca în laboratorul anterior) și modificați linia cuINITIALIZE_PASSînstatic RegisterPass<DCE> X(“mydce”, “My DCE Pass”);. - La execuție folosiți parametrul
loadcu calea către noul pass, ex:
opt -p -mem2reg -load ~packages/llvm-3.8.0/build/lib/libLLVMScalarOpts.a -mydce < test.bc > /dev/null
- Ce observați?
/* test.c */ #include <stdio.h> int test(int x) { int a, b, c; for (int i = 0; i < 1000000000; i++) { x = x + 1; a = x + 2; b = a - 3; c = a + b; x = x + 1; x = x + 1; x = x + 1; x = x + 1; x = x + 1; x = x + 1; x = a + b; x = a + b; x = a + b; x = a + b; x = a + b; x = a + b; } return 0; } int main() { int a = 1, b = 2; test(1); return 0; }
Exercițiul 2
Implementaţi analiza live variables. Algoritmul este explicat clar şi concis în Dragon book dar şi în slide-urile de aici. Puteţi pleca de la fişierul LiveVars.cpp din arhiva laboratorului. Pentru implementare, urmăriţi şi instrucţiunile din cod.
- ce reprezintă gen(B)/def(B)? Dar kill/use?
- explicaţi ecuaţia de flux pentru in(B)
- cum arată laticea? Indexaţi instrucţiunile pentru a putea reprezenta un element din latice ca vector de biţi (1)
- implementaţi calculul def (2) şi use (3)
- implementaţi algoritmul Killdal (4)
- rulati pass-ul peste urmatorul fisier dupa ce faceti transformara in forma SSA (dupa ce rulati pass-ul mem2reg).