This is an old revision of the document!
Laborator 4: Programare Dinamică
Responsabili: Darius Neațu, Răzvan Chițu
Obiective laborator
- Ințelegerea noțiunilor de bază despre programare dinamică
- Insușirea abilităților de implementare a algoritmilor bazați programare dinamică.
Precizari initiale
Acestea apar incorporate si in textul laboratorului pentru a facilita parcurgerea cursiva a laboratorului.
- Toate bucatile de cod prezentate in partea introductiva a laboratorului (inainte de exercitii) au fost testate. Cu toate acestea, este posibil ca din cauza mai multor factori (formatare, caractere invizibile puse de browser etc) un simplu copy-paste sa nu fie de ajuns pentru a compila codul.
- Va rugam sa incercati si codul din arhiva demo-lab04.zip, inainte de a raporta ca ceva nu merge. :D
- Pentru orice problema legata de continutul acestei pagini, va rugam sa dati email la neatudarius@gmail.com.
Ce este DP?
Similar cu greedy, tehnica de programare dinamica este folosită pentru rezolvarea problemelor de optimizare. In continuare vom folosi acronimul DP (dynamic programming).
Pentru restul notiunilor prezentate pana acum despre DP, va rugam sa consulati pagina laboratorului 3.
Exemple clasice
Programarea Dinamică este cea mai flexibilă tehnica din programare. Cel mai ușor mod de a o înțelege presupune parcurgerea cât mai multor exemple.
Propunem cateva categorii de recurente, pe care le vom grupa astfel:
- recurente de tip SSM
- recurente de tip RUCSAC
- recurente de tip PODM
- recurente de tip numărat
- recurente pe grafuri
Categoria 3: PODM
Aceste recurente au o oarecare asemanare cu problema PODM (enunt + solutie).
ATENTIE! Intrucat acest tip de recurente poate fi mai greu (decat celelalte), doar il vom mentiona. Puteti consulta acasa materialele puse la dispozitie pentru intelege si aceasta categorie.
Caracteristici:
- Acest tip de problema presupune ca o putem formula ca pe o problema de tip subinterval $[i, j]$.
- Daca dorim sa gasim optimul pentru acest interval, va trebuie sa luam in calcul toate combinatiile de 2 subproblemele care ar fi putut genera solutie pentru probleme $[i, j]$.
- Se considera fiecare divizare in 2 subprobleme, data de intermediarul k
- $[i, k]$ si $[k + 1, j]$ sunt cele 2 subprobleme pentru care cunoastem solutiile
- atunci o solutie pentru $[i,j]$ se poate obtine imbinandu-le pe cele doua
- ca sa gasim solutia cea mai buna
- vom itera prin toate valorile k posibile
- vom alege pe cea care maximizeaza solutia problemei $[i,j]$
- Calculul se face de la intervale mici (probleme usoare - $[i,i]$ sau $[i, i+1]$) spre probleme generale (dimensiune generala - $[i, j]$ ). In final se ajunge si la dimensiunile initiale ($[1, n]$).
Categoria 4: NUMARAT
Aceste recurente au o oarecare asemanare:
- toate numara lucruri! :p
- interesante sunt cazurile cand numarul cautat este foarte mare (altfel am putea apela la alte metode - ex. generarea tuturor candidatilor posibili cu backtracking)
- in acest caz, deoarece numarul poate sa nu incapa pe un tip reprezentabil standard (ex. int pe 32/64 de biti), se cere (de obicei) restul impartirii numarului cautat la un numar MOD (vom folosi in continuare aceasta notatie).
Regulile de lucru cu clase de resturi
Reamintim cateva proprietati matematice pe care ar trebui sa le aveti in vedere atunci in implementati pentru obtine corect resturile pentru anumite expresii. (corect poate sa insemne, de exemplu, sa evitati overflow :D - lucru neintuitiv cateodata).
- proprietati de de baza
- $(a + b) \ \% \ MOD = ((a \ \% \ MOD) + (b \ \% \ MOD)) \ \% \ MOD $
- $(a \ * b) \ \% \ MOD = ((a \ \% \ MOD) \ * (b \ \% \ MOD)) \ \% \ MOD $
- $(a - b) \ \% \ MOD = ((a \ \% \ MOD) - (b \ \% \ MOD) + MOD) \ \% \ MOD $ (restul nu poate fi ceva negativ; in C++ % nu functioneaza pe numere negative)
- invers modular
- $ \frac{a}{b} \ \% \ MOD = ((a \ \% \ MOD) * (b ^ {MOD-2} \ \% \ MOD)) \ \% \ MOD)$
- DACA MOD este prim; DACA a si b nu sunt multipli ai lui MOD
Gardurile lui Gigel
Enunt
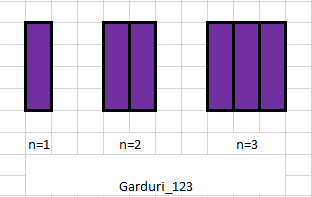
Gigel trece de la furat obiecte cu un rucsac la numarat garduri (fiecare are micile lui placeri :D). El doreste sa construiasca un gard folosind in mod repetat un singur tip de piesa.
O piesa are dimensiunile 4 x 1 (o unitate = 1m). Din motive irelevante pentru aceasta problema, orice gard construit trebuie sa aiba inaltime 4m in orice punct.
O piesa poate fi pusa in pozitie orizontala sau in pozitie verticala.
Cerinta
Gigel se intreaba cate garduri de lungime n si inaltime 4 exista? Deoarece celalalt prenume al lui este Bulănel, el intuieste ca acest numar este foarte mare, de aceea va cere restul impartirii acestui numar la 1009.
RECURENTA
NUMIRE RECURENTA
$dp[i] $ = numarul de garduri de lungime i si inaltime 4 (nimic special - exact ceeea ce se cere in enunt)
Raspunsul la problema este $dp[n]$.
GASIRE RECURENTA
- CAZ DE BAZA
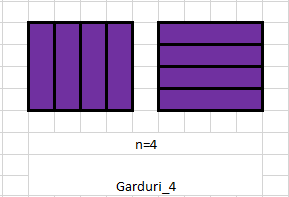
- $dp[1] = dp[2] = dp[3] = 1$; $dp[4]$ = 2
- CAZ GENERAL
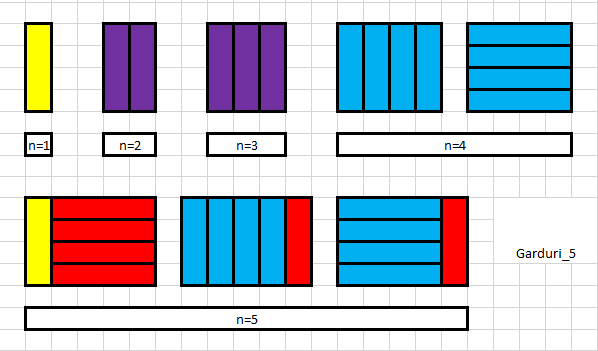
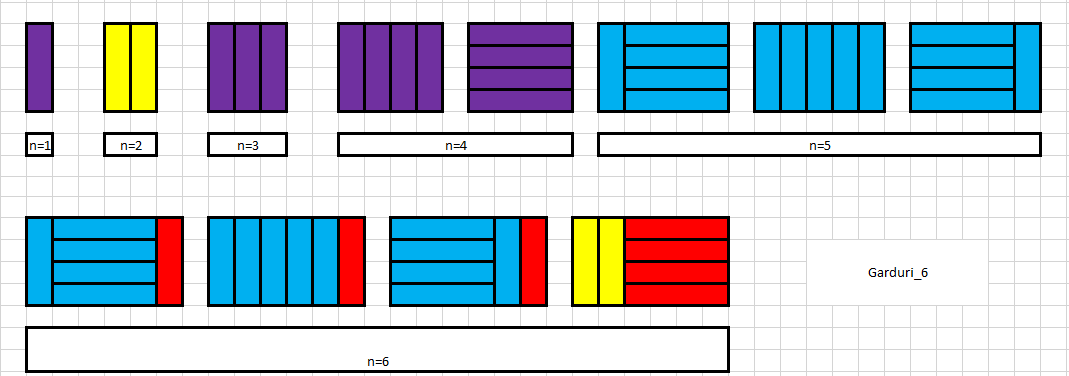
- atunci dorim sa formam un gard de lungime i ($ i >= 5 $) am vazut ca putem alege cum sa punem ultima/ultimele piese
- DACA alegem ca ultima piesa sa fie pusa in pozitie verticala, atunci la stanga mai ramane de completat un subgard de lungime $i-1$
- numarul de moduri in care putem face acest subgard este $dp[i-1]$
- DACA alegem ca ultima piesa sa fie in pozitie orizontala (de fapt punem 4 piese in pozitie orizontala), atunci la stanga mai ramane de completat un subgard de lungime $i-4$
- numarul de moduri in care putem face acest subgard este $dp[i-4]$
- $dp[i] = (dp[i-1] + dp[i-4]) \ \% \ MOD$
IMPLEMENTARE RECURENTA
Aici puteti vedea un exemplu simplu de implementare in C++.
Complexitate
- complexitate temporala: $T = O(n)$
- explicatie: avem o singura parcurgere in care construim tabloul dp
- se poate obtine $T=O(log n)$ folosind exponentiere pe matrice!
- complexitate spatiala: $S = O(n)$
- explicatie: stocam tabloul dp
- se poate ontine $S = O(1)$ folosind exponentiere pe matrice!
Tehnici folosite in DP
De multe ori este nevoie sa folosim cateva tehnici pentru a obtine performanta maxima cu recurenta gasita.
In laboratorul 3 se mentiona tehnica de memoizare (in prima parte a laboratorului). In acesta ne vom rezuma la cum putem folosi cunostintele de lucru matricial pentru a favorizarea implementarea unor anumite tipuri de recurente.
Exponentiere pe matrice pentru recurente liniare
Recurente liniare
O recurenta liniara in contextul laboratorului de DP este de forma:
- $dp[i] = \sum_{k=1}^{KMAX} c_k * dp[i - k]$
- pentru KMAX o constanta
- de obicei, KMAX este foarte mica comparativ cu dimensinea n a problemei
- $c_k$ constante reale (unele pot fi nule)
O astfel de recurenta ar insemna ca pentru a calcula costul problemei i , imbinam costurile problemelor $i - 1, i-2, ...., i-k$, fiecare contribuind cu un anumit coeficient $c_{1}, c_{2}, ..., c_{k}$.
Exponentiere pe matrice
Facem urmatoarele notatii:
- $S_i$ = starea la pasul i
- $S_i = (dp[i - k + 1], dp[i - k + 2], ..., dp[i - 1], dp[i])$
- $S_k$ = starea initiala (in care cunoaste cele k cazuri de baza)
- $S_k = (dp[1], dp[2], ..., dp[k-1], dp[k])$
- $C$ = matrice ce coeficienti constanti
- are dimensiune $KMAX * KMAX$
- putem pune constante in clar
- putem pune constantele $c_k$ care tin de problema curenta
Algoritm naiv
Putem formula problema astfel:
- $S_k$ = este starea initiala
- pentru a obtine starea urmatoare, aplicam algoritmul urmator
- $S_i = S_{i-1}C$
Determinare C
Pentru a determina elementele matricei C, trebuie sa ne uitam la inmultirea matriceala de mai sus si sa alegem elementele lui C astfel incat prin inmultirealui $S_{i-1}$ cu $C$ sa obtinem elementele din $S_i$.
\begin{gather} \begin{bmatrix} dp[i - k + 1] & ... & dp[i-1] & dp[i] \\ \end{bmatrix} = \begin{bmatrix} dp[i - k] & ... & dp[i-2] & dp[i-1] \\ \end{bmatrix} \begin{bmatrix} 0 & 0 &... & 0 & 0 & c_{k}\\ 1 & 0 &... & 0 & 0 & c_{k-1}\\ 0 & 1 &... & 0 & 0 & c_{k-2}\\ ... & ... & ... & ... & ...\\ 0 & 0 &... & 1 & 0 & c_{2}\\ 0 & 0 &... & 0 & 1 & c_{1}\\ \end{bmatrix} \end{gather}
Exponentiere logaritmica pe matrice
Algoritmul naiv de mai sus are dezavantajul ca are tot o complexitate temporala $O(n)$.
Sa executam cativa pasi de inductie pentru a vedea cum este determinat $S_i$. $$S_i = S_{i-1}C$$ $$S_i = S_{i-2}C^2$$ $$S_i = S_{i-3}C^3$$ $$...$$ $$S_i = S_{k}C^{i -k}$$
In laboratorul 2 (Divide et Impera) am invatat ca putem calcula $ x ^ n $ in timp logaritmic. Deoarece si inmultirea matricilor este asociativa, putem calcula $C ^ n$ in timp logaritmic.
Obtinem astfel o solutie cu urmatoarele complexitati:
- complexitate temporala : $T = O(KMAX^3 * log(n))$
- explicatie
- facem doar $O(log n)$ pasi, dar un pas implica inmultire de matrice
- o inmultire de matrice patratica de dimensiune KMAX are $KMAX^3$ operatii
- aceasta metoda este eficienta cand $KMAX << n$ (KMAX este mult mai mic decat n)
- complexitatea spatiala : $M = O(KMAX^3)$
- explicatie
- este nevoie sa stocam cateva matrici
Observatie! In ultimele calcule nu am sters contanta KMAX, intrucat apare la puterea a 3-a! $KMAX = 100$ implica $KMAX^3 = 10^6$, valoare care nu mai poate fi ignorata in practica ($KMAX^3$ poate fi comparabil cu n).
Gardurile lui Gigel (optimizare)
Dupa cum am vazut mai sus, in problema cu garduri data de gigel solutia este o recurenta liniara:
- $dp[1] = dp[2] = dp[3] = 1$; $d[4]=2$;
- $dp[i] = dp[i - 1] + dp[i - 4]$, pentru $i > 4$
Exponentiere rapida :p
- $ k = 4 $
- $S_4 = (dp[1], dp[2], dp[3], dp[4]) = (1, 1, 1, 4)$
- $S_i = (dp[i-3], dp[i-2], dp[i-1], dp[i])$
- Raspunsul se afla efectuand operatia $S_n = S_4 * C^{n - 4}$, unde C are urmatorul continut:
\begin{gather} C = \begin{bmatrix} 0 & 0 & 0 & 1\\ 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 1\\ \end{bmatrix} \end{gather}
Exercitii
Azerah
Exponentiere
BONUS - TODO
Referințe
[0] Capitolul Dynamic Programming din Introductions to Algorithms de către T. H. Cormen, C. E. Leiserson, R. L. Rivest, C. Stein
[1] http://infoarena.ro/problema/podm